Engee documentation
Notebook

Reading data from Excel format and building models

Very often, the data that needs to be analyzed is not taken from some abstract repositories or databases, but lies in some kind of tabular format file. In some industries, CSV is the preferred format; in other cases, data is created in standard tabular editors.

In this demo, we will learn how to load and display data from an Excel spreadsheet on a graph and build a model based on it.

Reading an entire file

For most commands, we will need the following libraries, which are already built into the environment. It only remains for us to indicate that we are going to use commands from the namespace of these libraries.

In [ ]: 
Pkg.add(["Interpolations", "XLSX", "GLM", "Optim"])
In [ ]: 
using XLSX, DataFrames

One Excel file can contain several sheets with tables. Most often, we use only the first of these sheets, which is called Лист1 or Sheet1 (but it may be called something else).

Reading the entire file will return us an object with several tables inside, each of which is located on a separate sheet.

In [ ]: 
xf = XLSX.readxlsx( "table_simple_example.xlsx" )
Out[0]:
XLSXFile("table_simple_example.xlsx") containing 1 Worksheet
            sheetname size          range        
-------------------------------------------------
                Лист1 4x3           A1:C4

We can verify this again by displaying the list of sheets.

In [ ]: 
XLSX.sheetnames(xf)
Out[0]:
1-element Vector{String}:
 "Лист1"

If you have already opened the file with the command readxlsx then you can separate the desired sheet using an additional command.

In [ ]: 
sh = xf["Лист1"]
Out[0]:
4×3 XLSX.Worksheet: ["Лист1"](A1:C4)

Or you can use commands that perform this process faster.

Reading a separate sheet from a table

Standards by library teams XLSX you can read each sheet individually.

In [ ]: 
XLSX.readtable( "table_simple_example.xlsx", "Лист1" )
Out[0]:
XLSX.DataTable(Any[Any[1, 4, 7], Any[2, 5, 8], Any[3, 6, 9]], [:a, :b, :c], Dict(:a => 1, :b => 2, :c => 3))

You can put a sheet of the table in the format DataFrame and process the data using this library.

In [ ]: 
DataFrame( XLSX.readtable( "table_simple_example.xlsx", "Лист1" ) )
Out[0]:

3 rows × 3 columns

abc
AnyAnyAny
1123
2456
3789
In [ ]: 
xdf = Float32.(DataFrame( XLSX.readtable( "table_simple_example.xlsx", "Лист1" ) ))
Out[0]:

3 rows × 3 columns

abc
Float32Float32Float32
11.02.03.0
24.05.06.0
37.08.09.0

But it makes sense when the data is a set of objects and a list of their attributes. Sometimes the table contains just a matrix with numbers, and then it's better to work with it using a standard data type. Matrix.

In [ ]: 
xm = XLSX.readdata( "table_simple_example.xlsx", "Лист1", "A2:C4" )
Out[0]:
3×3 Matrix{Any}:
 1  2  3
 4  5  6
 7  8  9

Choosing the right data type greatly simplifies further work with the table or matrix.

In [ ]: 
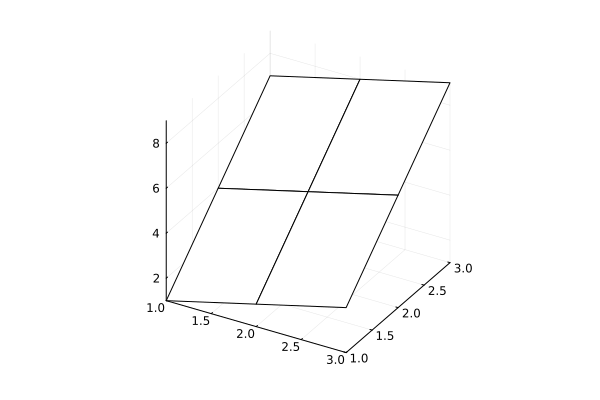
gr()
wireframe( xm )
Out[0]:

Calculating data on a new computational grid (interpolation)

Now, we have at our disposal a table of data set in a certain coordinate system, we can perform their interpolation using a spline and build a model.

In [ ]: 
xm = vec( Float32.( XLSX.readdata("table_matrix_example.xlsx", "Лист1", "B1:D1") ))
ym = vec( Float32.( XLSX.readdata("table_matrix_example.xlsx", "Лист1", "A2:A4") ))
zm = Float32.( XLSX.readdata("table_matrix_example.xlsx", "Лист1", "B2:D4") )

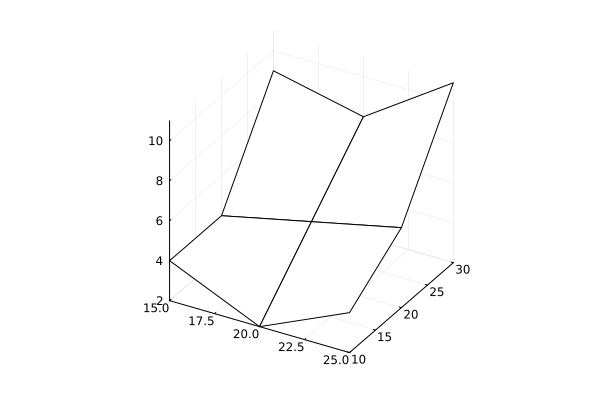
wireframe( xm, ym, zm )
Out[0]:
In [ ]: 
using Interpolations

# Переводим описание системы координат из векторов в набор диапазонов
xSrc = range( minimum(xm), maximum(xm), step=xm[2]-xm[1] )
ySrc = range( minimum(ym), maximum(ym), step=ym[2]-ym[1] )

# Строим модель, которая предскажет нам значения на новой сетке
cubInt = cubic_spline_interpolation( (xSrc, ySrc), zm )

# Задаем новую расчетную сетку
xRange = range( minimum(xm), maximum(xm), 50 )
yRange = range( minimum(ym), maximum(ym), 50 )
zIntRes = cubInt(xRange, yRange)

# Визуализируем результат
surface( xRange, yRange, zIntRes, fillalpha=0.2 )
wireframe!( xRange, yRange, zIntRes )
Out[0]:

We performed cubic spline interpolation. If the original data points were located in the coordinate system, but with irregular serifs along the X and Y axes, then we would only be able to build a model based on linear interpolation (or the "nearest neighbor method" model).

Function approximation and minimum search

After visual analysis of the data, you can make an assumption about which function would be convenient to approximate this data. This requires some experience and interactive work with the data.

Let's assume that we have made sure that the data is well represented using a quadratic function. Let's construct a polynomial that will allow us to more accurately find the estimated values of the output parameters in which the target value of the process under study is minimal.

In [ ]: 
using GLM

# Подготовим данные: представим таблицу как список отдельных точек данных
xx = Float64.(repeat( collect(xSrc), outer = length(ySrc) ))
yy = Float64.(repeat( collect(ySrc), inner = length(xSrc) ))
zz = Float64.(vec(reshape(zm', 1, :)))

# Создадим объект DataFrame
data = DataFrame( X = xx, Y = yy, Z = zz )

# Построим модель с двумя входными параметрами
model = lm( @formula(Z ~ X + Y + X^2 + Y^2 + X*Y), data )
Out[0]:
StatsModels.TableRegressionModel{LinearModel{GLM.LmResp{Vector{Float64}}, GLM.DensePredChol{Float64, LinearAlgebra.CholeskyPivoted{Float64, Matrix{Float64}, Vector{Int64}}}}, Matrix{Float64}}

Z ~ 1 + X + Y + :(X ^ 2) + :(Y ^ 2) + X & Y

Coefficients:
──────────────────────────────────────────────────────────────────────────────
                  Coef.   Std. Error      t  Pr(>|t|)    Lower 95%   Upper 95%
──────────────────────────────────────────────────────────────────────────────
(Intercept)  26.1111     10.0158       2.61    0.0799  -5.76373     57.986
X            -2.2         0.96622     -2.28    0.1072  -5.27494      0.874942
Y            -0.433333    0.292604    -1.48    0.2352  -1.36453      0.497864
X ^ 2         0.0533333   0.0237268    2.25    0.1102  -0.0221761    0.128843
Y ^ 2         0.0133333   0.00593171   2.25    0.1102  -0.00554402   0.0322107
X & Y         0.01        0.0083887    1.19    0.3189  -0.0166966    0.0366966
──────────────────────────────────────────────────────────────────────────────
In [ ]: 
# Задаем новую расчетную сетку
dx = 2 * abs(maximum(xm) - minimum(xm))
dy = 2 * abs(maximum(ym) - minimum(ym))
xRange = range( minimum(xm) - dx, maximum(xm) + dx, 50 )
yRange = range( minimum(ym) - dy, maximum(ym) + dy, 20 )

# Визуализируем результат
xx = repeat( collect(xRange), outer = length(yRange) )
yy = repeat( collect(yRange), inner = length(xRange) )
zz = reshape( GLM.predict(model, (;X=xx,Y=yy)), length(xRange), :)

# Построим графики
surface( xRange, yRange, zz', fillalpha=0.2, xlabel="x", ylabel="y", zlabel="z" )
wireframe!( xRange, yRange, zz' )
Out[0]:

Models created using GLM they take a point cloud as input (as you saw, we used data in the form of one-dimensional vectors Vector) and allow you to perform extrapolation without any additional settings.

Finding the minimum point

Both objects allow us to find the minimum point of the function, the description of which we obtained from the table.

In [ ]: 
using Optim
opt = optimize( x->GLM.predict( model,(;X=[x[1]],Y=[x[2]]) )[1], [0.0,0.0] )
(x_min, y_min) = Optim.minimizer( opt )

surface( xRange, yRange, zz', xlabel="x", ylabel="y", zlabel="z", c=:viridis, zcolor=zz' )
scatter!( [x_min], [y_min], [GLM.predict( model,(;X=[x_min],Y=[y_min]) )[1]],
    camera = (30,50), legend=false, cbar=false )
Out[0]:

We have received a graph where the minimum is marked.

Writing data to an Excel file

To save the analysis results to another Excel spreadsheet, use the following command:

In [ ]: 
XLSX.openxlsx( "table_write_example_1.xlsx", mode="w" ) do xf
    
    # Поместим матрицу на первый лист
    XLSX.rename!( xf[1], "Лист1" )

    xw = reshape(xx, 1, :) # Сделаем матрицы из векторов
    for ind in CartesianIndices(xw)
        XLSX.setdata!( xf["Лист1"], XLSX.CellRef( ind[1], ind[2]+1 ), xw[ind])
    end

    yw = reshape(yy, :, 1)
    for ind in CartesianIndices(yw)
        XLSX.setdata!( xf["Лист1"], XLSX.CellRef( ind[1]+1, ind[2] ), yw[ind])
    end

    zw = zz
    for ind in CartesianIndices(zw)
        XLSX.setdata!( xf["Лист1"], XLSX.CellRef( ind[1]+1, ind[2]+1 ), zw[ind])
    end

    
    # На второй лист поместим DataFrame
    XLSX.addsheet!( xf, "Лист2" )
    XLSX.writetable!( xf["Лист2"], eachcol(xdf), names(xdf); anchor_cell=XLSX.CellRef("A1"))
    
end

Or, much shorter, to save DataFrame in a single-sheet table:

In [ ]: 
XLSX.writetable( "table_write_example_2.xlsx", xdf, overwrite=true )

To save objects Matrix or Vector The tabular format is much more commonly used CSV.

Conclusion

In this example, we learned how to read files in Excel tabular format. We converted them to different formats.:

  • format DataFrame which is best suited for analyzing tabular data
  • format Matrix, which allows you to work with a group of numbers from the source table as a matrix

We also demonstrated how to perform interpolation and approximation of data read from an Excel file and how to save the results.