Engee documentation
Notebook

Regression using a multi-layered neural network

In this work, we will need to train a neural network to predict the output of a continuous function from two parameters and place it on the Engee canvas as another block. For example, as a surrogate model to replace some complex subsystem.

Data description

Our data is generated by a process of the form :

In [ ]: 
Pkg.add(["JLD2", "Flux"])
In [ ]: 
Nx1, Nx2 = 30, 40
x1 = Float32.( range( -3, 3, length=Nx1 ) )
x2 = Float32.( range( -3, 3, length=Nx2 ) )
Xs = [ repeat( x1, outer=Nx2)  repeat( x2, inner=Nx1) ];
# The first example of the output data
Ys = @. 3*(1-Xs[:,1])^2*exp(-(Xs[:,1]^2) - (Xs[:,2]+1)^2) - 10*(Xs[:,1]/5 - Xs[:,1]^3 - Xs[:,2]^5)*exp(-Xs[:,1]^2-Xs[:,2]^2) - 1/3*exp(-(Xs[:,1]+1) ^ 2 - Xs[:,2]^2);
# The second example of the output data
# Ys = @. 1*(1-Xs[:,1])^2*exp(-(Xs[:,1]^2) - (Xs[:,2]+1)^2) - 15*(Xs[:,1]/5 - Xs[:,1]^3 - Xs[:,2]^6)*exp(-Xs[:,1]^2-Xs[:,2]^2) - 1/3*exp(-(Xs[:,1]+1) ^ 2 - Xs[:,2]^2);

Xs – matrix size 1200x2 (in a sample of 1,200 examples, each is characterized by two features: x1 and x2)

Ys – matrix size 1200х1 (forecast column)

The learning process

Let's set the parameters for the training procedure and run a fairly simple version of the cycle.

In [ ]: 
# @markdown ## Configuring neural network parameters
# @markdown *(double click allows you to hide the code)*
# @markdown
Параметры_по_умолчанию = false # @param {type: "boolean"}
if Parameters_to Silence
    Learning rate Coefficient = 0.01
    Number of Training cycles = 2000
else
    Количество_циклов_обучения = 2001 # @param {type:"slider", min:1, max:2001, step:10}
    Коэффициент_скорости_обучения = 0.08 # @param {type:"slider", min:0.001, max:0.5, step:0.001}
end

epochs = Number of Training Cycles;
learning_rate = Learning rate Coefficient;

Let's create a neural network with two inputs, two intermediate states (sizes 20 and 5) and one output. It is important that the output of the neural network has a linear activation function.

In [ ]: 
using Flux
model = Chain( Dense( 2 => 20, relu ),      # The structure of the model that we will train
               Dense( 20 => 5, relu ),
               Dense( 5 => 1 ) )
data = [ (Xs', Ys') ]                       # Setting the data structure
loss( ỹ, y ) = Flux.mse( ỹ, y )             # and the loss function to which they will be transferred by the training procedure
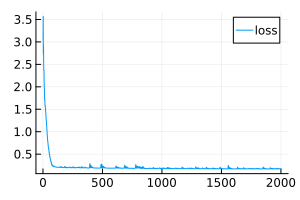
loss_history = []                           # We will keep the learning history
opt_state = Flux.setup( Adam( learning_rate ), model ); # Optimization algorithm
for i in 1:epochs
    Flux.train!( model, data, opt_state) do m, x, y
        loss( m(x), y ) # Loss function - error on each element of the dataset
    end
    push!( loss_history, loss( model(Xs'), Ys' ) ) # Let's remember the value of the loss function
end
plot( loss_history, size=(300,200), label="loss" ) # Let's get a chronicle of the training
Out[0]:

Transferring the neural network to the Engee canvas

In the variable model the newly trained neural network is stored.

We recreated its structure using elements on canvas.:

image.png

☝️ Our model requires a variable model, from where it gets the parameters. If there is no such variable, the model will try to find the file. model.jld2 in the home directory. If this file is not found, the model will create an empty neural network with random parameters.

Fully connected layers assembled from the most common blocks Product and Add, which performs multiplication of inputs by a matrix and addition of a displacement vector.

image.png

Activation functions, for greater clarity, are not hidden inside the layers, but brought out.

image.png

Let's run this model on a set of several hundred random points.

In [ ]: 
if "neural_regression_multilayer" ∉ getfield.(engee.get_all_models(), :name)
    engee.load( "$(@__DIR__)/neural_regression_multilayer.engee");
end
model_data = engee.run( "neural_regression_multilayer" );

The model returns us a matrix of matrices. You can fix this by using canvas blocks, or you can implement your own version of the function. flatten:

In [ ]: 
model_x1 = model_data["X1"].value;
model_x2 = model_data["X2"].value;
model_y = vec( hcat( model_data["Y"].value... ));

We display the results

In [ ]: 
gr()

plot(
    surface( Xs[:,1], Xs[:,2], vec(Ys), c=:viridis, cbar=:false, title="Training sample", titlefont=font(10)),
    wireframe( x1, x2, vec(model( Xs' )), title="Forecast from a neural network (via a script)", titlefont=font(10) ),
    scatter( model_x1, model_x2, model_y, ms=2.5, msw=.5, leg=false, zcolor=model_y,
        xlimits=(-3,3), ylimits=(-3,3), title="The forecast from the model on the canvas", titlefont=font(10) ),
    layout=(1,3), size=(1000,400)
)
Out[0]:

Saving the model

Finally, we will save the trained neural network to a file if this file is missing.

In [ ]: 
if !isfile( "model.jld2" )
    using JLD2
    jldsave("model.jld2"; model)
end

Conclusion

We have trained a multi-layered neural network consisting of three fully connected layers. Then we transferred all its coefficients to the canvas for use in a convenient model-oriented context* (more convenient than working with neural networks through code)*.

This work is easy to repeat with any tabular data and scale the neural network to meet the needs of the project. Saving the trained network to a file allows you to execute the model along with other elements of the Engee diagram without re-training the neural network.

If desired, weights and offsets can be written in blocks. Constant on the canvas and get a block with a neural network, regardless of the file availability model.jld2.

Blocks used in example