Engee documentation
Notebook

Engee Graph Gallery

In this set of examples, we will show what the most diverse types of graphs look like in Engee, and by what means such a result is achieved – examples of data and code.

The right type of schedule allows you to save or convey the necessary information to the listener in a very eloquent, yet concise form. Graphs take information from variables that should exist in the memory workspace (_ should be visible in the Variables window_). They are usually displayed from interactive ngscript scripts, immediately after the corresponding code cells. Of course, there are exceptions.

  • Unicode graphics can also be displayed on the command line, however, if interactive graphics are available, such a limited format may be needed only for the needs of special graphic design.;
  • Graphs can be saved to file storage and opened as files from a file browser (sometimes useful).

The simplest and most frequently used command for displaying graphs is the function plot() from the library Plots for displaying graphs.

The Plots library in Engee is connected automatically.

At the same time, there are many more libraries in the Engee/Julia ecosystem for displaying beautiful graphs, some of which we will look at in this demo.:

  • StatsPlots for displaying complex statistical graphs,
  • GMT or General Mapping Tools for displaying geographical maps.

We also advise you not to avoid libraries that allow you to create much richer and more professional visualizations, for example:

  • Makie for very high-quality visualization of complex data,
  • Luxor – a language for creating vector two-dimensional graphics.

When the output library has built a graph, it transmits it to the graphical environment, and there are options here.:

  • environment gr (which is enabled by default) builds fast, economical and non-interactive graphs (enabled by the command gr()), which can be saved using the context menu
  • plotly or plotlyjs they create an interactive canvas on which the graph can be scaled, rotated and saved using the interface buttons (you can switch to them, respectively, with commands plotly() and plotlyjs())

You can also choose a bitmap for displaying graphs (png) or vector (svg) format. By specifying inside the commands gr/plotly/plotlyjs argument fmt=:svg you will get a very elegant, scalable graph in vector format, however, if there are a large number of elements on the graph, especially if it is interactive, its output will require more resources. Raster graphics are another matter (fmt=:png). They build faster and do not require such resources when redrawing.

You will find the rest of the recipe elements for the perfect schedule below.

In [ ]: 
Pkg.add(["StatsPlots", "WordCloud", "MeshIO", "ColorSchemes", "Colors", "GMT", "Statistics", "StatsBase", "CSV", "Distributions", "Meshes"])
In [ ]: 
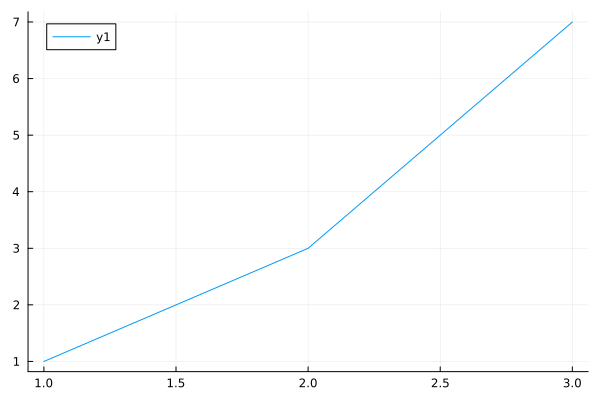
gr()
plot([1,2,3], [1,3,7])
Out[0]:

Data analysis

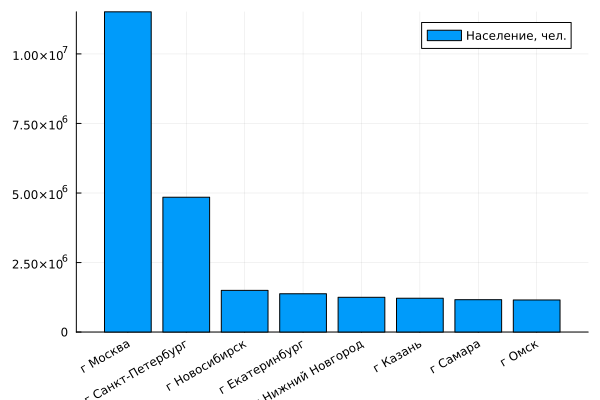
Building a bar chart based on a data table.

In [ ]: 
using DataFrames, HTTP, CSV;

# Open data from a file
data = sort( CSV.File( "data/city.csv" ) |> DataFrame, ["population"], rev=true );

# (or) Download data from the server
# url = "https://raw.githubusercontent.com/hflabs/city/master/city.csv"
# data = sort( CSV.File( HTTP.get(url).body) |> DataFrame, ["population"], rev=true );

bar( first(data, 8).population, label="Population, people", xrotation = 30 )
xticks!( 1:8, first(data, 8).address )
Out[0]:

Studying the correlation of multidimensional data using the library StatsPlots and functions corrplor.

In [ ]: 
using StatsPlots, DataFrames, LaTeXStrings

M = randn( 1000, 4 )
M[:,2] .+= 0.8sqrt.(abs.(M[:,1])) .- 0.5M[:,3] .+ 5
M[:,3] .-= 0.7M[:,1].^2 .+ 2
corrplot( M, label = [L"$x_i$" for i=1:4],
          xtickfontsize=4, ytickfontsize=6,
          guidefontcolor=:blue, yguidefontsize=15, yguidefontrotation=-45.0 )
Out[0]:

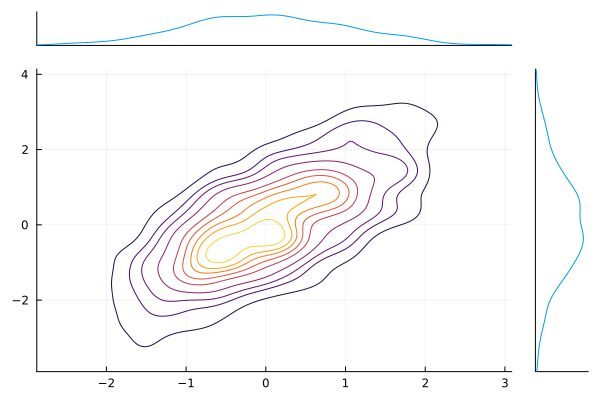
Function marginalkde from the library StatsPlots

In [ ]: 
using StatsPlots

x = randn(1024)
y = randn(1024)
marginalkde(x, x+y)
Out[0]:
In [ ]: 
using DataFrames, Statistics

# Creating the data
df = DataFrame(Age=rand(4), Balance=rand(4), Position=rand(4), Salary=rand(4))
cols = [:Возраст, :Баланс, :Должность]  # Let's select a part of the data
M = cor(Matrix(df[!,cols]))       # The covariance matrix

# Chart
(n,m) = size(M)
heatmap( M, fc=cgrad([:white,:dodgerblue4]), xticks=(1:m,cols), xrot=90, yticks=(1:m,cols), yflip=true, leg=false )
annotate!( [(j, i, text(round(M[i,j],digits=3), 10,"Arial",:black)) for i in 1:n for j in 1:m] )
Out[0]:
1.0 -0.033 -0.388 -0.033 1.0 -0.893 -0.388 -0.893 1.0

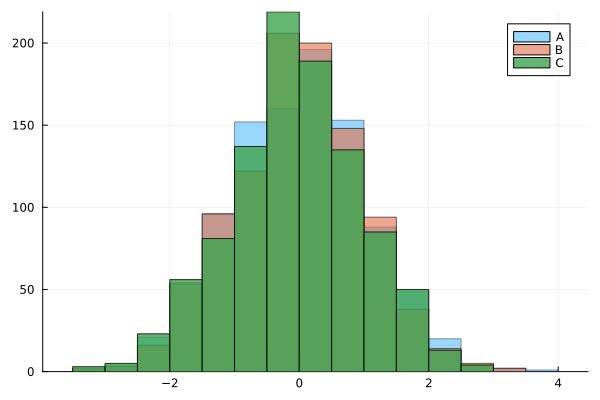
The usual histogram: function histogram

In [ ]: 
using Random
Random.seed!(2018)

x = randn(1000)
y = randn(1000)
z = randn(1000)

histogram(x, bins=20, alpha=0.4, label="A")
histogram!(y, bins=20, alpha=0.6, label="B")
histogram!(z, bins=20, alpha=0.8, label="C")
Out[0]:

Two-dimensional sample distribution graph: function histogram2d

In [ ]: 
x = randn(10^4)
y = randn(10^4)

histogram2d(x, y)
Out[0]:

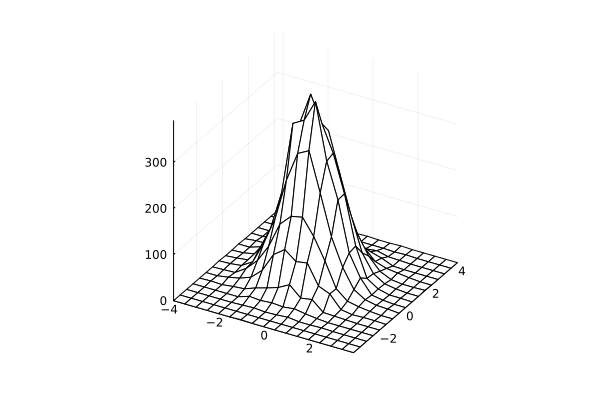
Volumetric graph of a two-dimensional histogram using wireframe

In [ ]: 
using StatsBase

x = randn(10^4)
y = randn(10^4)
h = StatsBase.fit( Histogram, (x, y), nbins=20 )

wireframe( midpoints(h.edges[1]), midpoints(h.edges[2]), h.weights )
Out[0]:

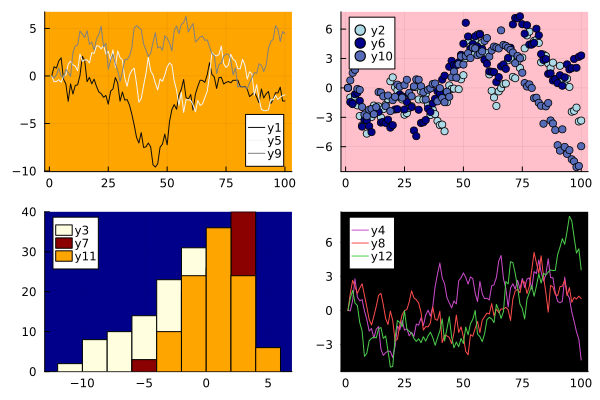
Combining schedules with different designs

In [ ]: 
using Random

Random.seed!(1)
plot( Plots.fakedata(100, 12),
      layout = 4,
      palette = cgrad.([:grays :blues :heat :lightrainbow]),
      bg_inside = [:orange :pink :darkblue :black],
      seriestype= [:line :scatter :histogram :line] )
Out[0]:

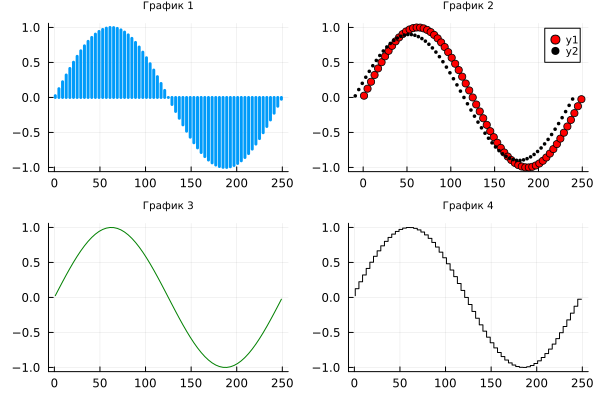
And just different types of graphs.:

In [ ]: 
x = 1:4:250;
y = sin.( 2pi/250 * x );

p1 = plot( x, y, title= "Schedule 1", seriestype=:stem, linewidth=3, legend=false )
p2 = plot( x, y, title= "Schedule 2", seriestype=:scatter, color=:red )
  plot!( p2, x .- 10, 0.9y, seriestype=:scatter, color=:black, markersize=2 )
p3 = plot( x, y, title= "Schedule 3", seriestype=:line, color=:green, legend=false )
p4 = plot( x, y, title= "Schedule 4", seriestype=:steppre, color=:black, leg=false )

plot( p1, p2, p3, p4, layout=(2,2), titlefont=font(7), legendfont=font(7) )
Out[0]:

Wordcloud:

In [ ]: 
import Pkg; Pkg.add(["WordCloud"], io=devnull);
using WordCloud, HTTP

# Upload text from a file
content = read( open("data/Wikipedia - Математика.txt", "r"), String )

# Or download the data from the server
# url = "https://ru.wikipedia.org/wiki/Mathematics"
# resp = HTTP.request("GET", url, redirect=true)
# content = resp.body |> String |> html2text

stopwords = ["XVII", "that", "frac"];
stopwords = vcat(stopwords, string.(collect(1:100)));

wc = wordcloud( processtext( content, maxnum=100, stopwords=stopwords, minlength=4 ),
    mask=shape(ellipse, 600, 400, color=(0.98, 0.97, 0.99), backgroundcolor=1, backgroundsize=(700, 550)),
    masksize=:original, colors=:seaborn_icefire_gradient, angles=[0] ) |> generate!
paint(wc, "$(@__DIR__)/fromweb.svg")
wc
Out[0]:

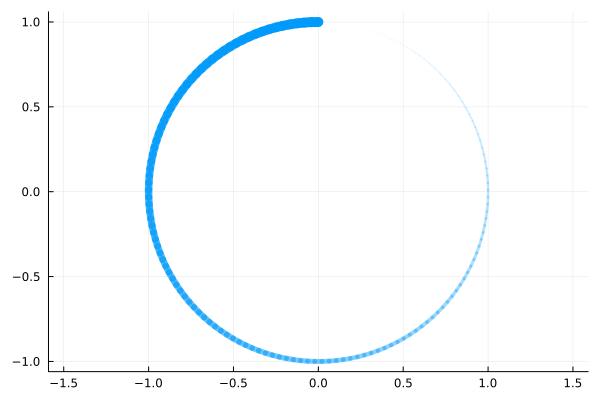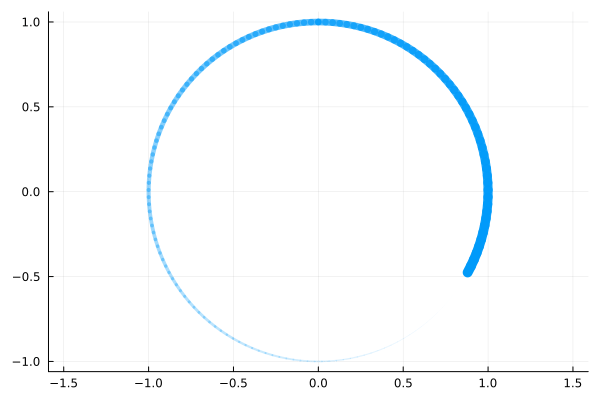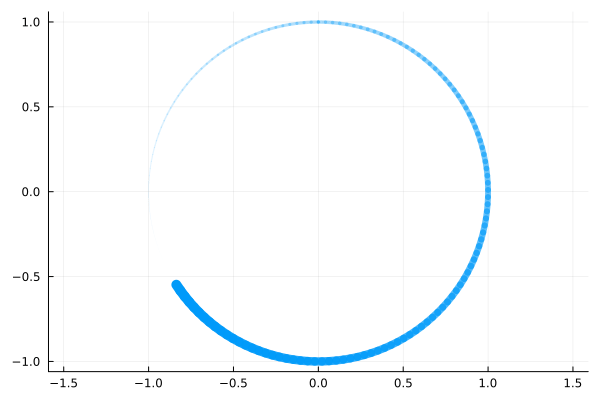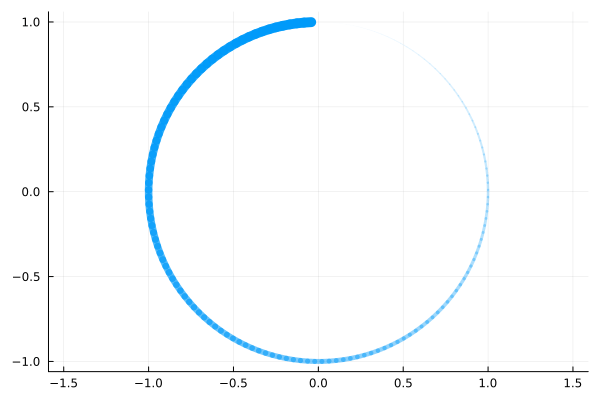
Animation

Creating GIF animations using the command @animate, which runs a third-party function in a loop that draws 150 circles of decreasing radius, with increasing transparency. Among others, you can also use the format mp4.

In [ ]: 
@userplot CirclePlot
@recipe function f(cp::CirclePlot)
    x, y, i = cp.args
    n = length(x)
    inds = circshift(1:n, 1 - i)
    linewidth --> range(0, 10, length = n)
    seriesalpha --> range(0, 1, length = n)
    aspect_ratio --> 1
    label --> false
    x[inds], y[inds]
end

n = 150
t = range(0, 2π, length = n)
x = sin.(t)
y = cos.(t)

anim = @animate for i ∈ 1:n
    circleplot(x, y, i)
end
gif(anim, "$(@__DIR__)/anim_fps15.gif", fps = 15)
Out[0]:
No description has been provided for this image

Rotating object (geometry is specified in the STL file)

In [ ]: 
import Pkg; Pkg.add(["Meshes", "MeshIO"], io=devnull);
using Meshes, MeshIO, FileIO
gr();

obj = load( "$(@__DIR__)/data/lion.stl" );

@gif for az in 0:10:359
    p = plot( camera = (az, -20), axis=nothing, border=:none, aspect_ratio=:equal, size=(400,400) )
    for i in obj
        m = Matrix([i[1] i[2] i[3] i[1]])'
        if m[1,1] > 0 plot!( p, m[:,1], m[:,2], m[:,3], lc=:green, label=:none, lw=.4, aspect=:equal )
        else plot!( p, m[:,1], m[:,2], m[:,3], lc=:gray, label=:none, lw=.4, aspect=:equal )
        end
    end
end

[ Info: Saved animation to /user/start/examples/data_analysis/plots_gallery/tmp.gif
Out[0]:
No description has been provided for this image

Conclusion of matrices and images

Function heatmap

In [ ]: 
include( "$(@__DIR__)/data/peaks.jl" );

(x, y, z) = peaks()
heatmap(x, y, z)
Out[0]:
In [ ]: 
using LaTeXStrings

x = range( -1.3, 1.3, 501 );
y = range( -1.3, 1.3, 501 );

X = repeat( x, outer = [1,501] )
Y = repeat( y', outer = [501,1] )

# C = ones( size(X) ) .* ( 0.360284 + 0.100376*1im );
C = ones( size(X) ) .* ( -0.75 + 0.1im );

Z_max = 1e6; it_max = 50;

Z = Complex.( X, Y );
B = zeros( size(C) );

for k = 1:it_max
    Z = Z.^2 .+ C;
    B = B .+ ( abs.(Z) .< 2 );
end

heatmap( B,
         aspect_ratio = :equal,
         cbar=false,
         axis=([], false),
         color=:jet )
title!( L"Julia Set $(c=0.360284+0.100376i)$" )
Out[0]:

Output of illustrations from files: library Images

In [ ]: 
using Images

load( "$(@__DIR__)/data/640px-Business_Centre_of_Moscow_2.jpg" )
Out[0]:
No description has been provided for this image

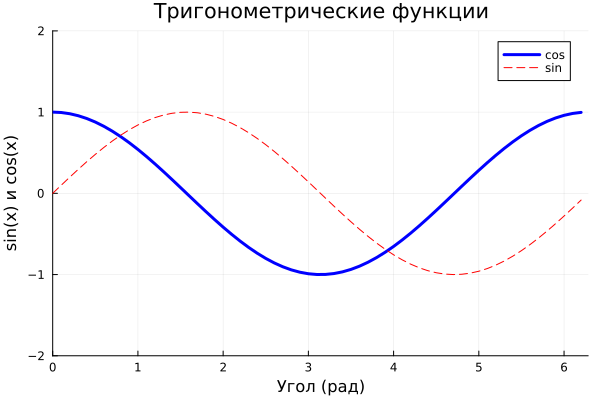
Graphs in Cartesian coordinates

Output of two trigonometric functions defined by vectors on a Cartesian coordinate plane.

In [ ]: 
x = 0:0.1:2pi
y1 = cos.(x)
y2 = sin.(x)

plot(x, y1, c="blue", linewidth=3, label="cos")
plot!(x, y2, c="red", line=:dash, label="sin")
title!("Trigonometric functions")
xlabel!("Angle (rad)")
ylabel!("sin(x) and cos(x)")

# Using a separate command, set the axis boundaries.
plot!( xlims=(0,2pi), ylims=(-2, 2) )
Out[0]:

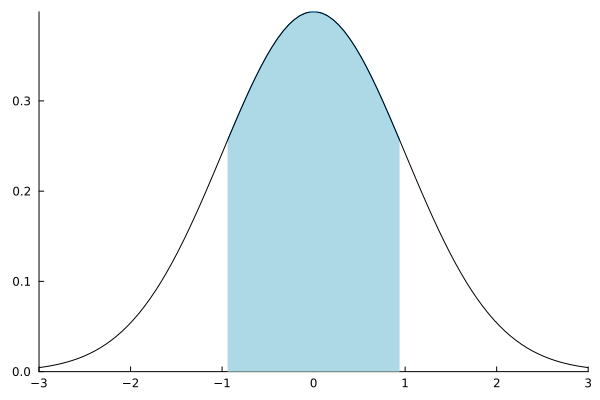
Filling in the area under the graph (argument fillrange)

In [ ]: 
using Distributions

x = range(-3, 3, 100 )
y = pdf.( Normal(0,1), x )

ix = abs.(x) .< 1
plot( x[ix], y[ix], fillrange = zero(x[ix]), fc=:blues, leg=false)
plot!( x, y, grid=false, lc=:black, widen=false )

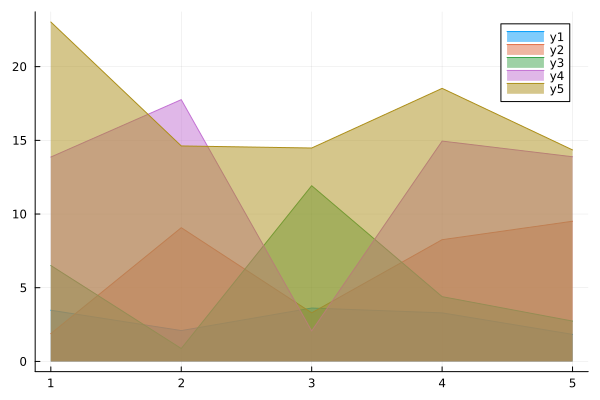
WARNING: using Distributions.shape in module Main conflicts with an existing identifier.
Out[0]:

Schedule to fill in (area)

In [ ]: 
x = 1:10;
areaData = x .* rand(10,5) .* 5;
cur_colors = theme_palette(:default)

plot()
for i in 1:size(areaData,2)
    plot!( areaData[i,:], fillcolor = cur_colors[i], fillrange = 0, fillalpha=.5 )
end
plot!()
Out[0]:

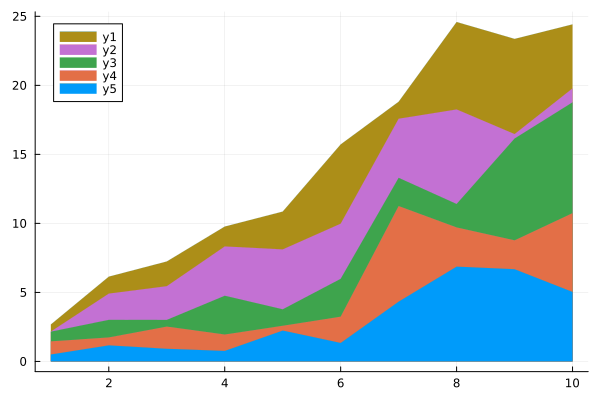
An accumulating schedule with filling in

In [ ]: 
x = 1:10;
areaData = x .* rand(10,5);
cur_colors = theme_palette(:default)

plot()
for i in size(areaData,2):-1:1
    plot!( sum(areaData[:,1:i], dims=2), fillcolor = cur_colors[i], fillrange = 0, lw=0 )
end
plot!()
Out[0]:

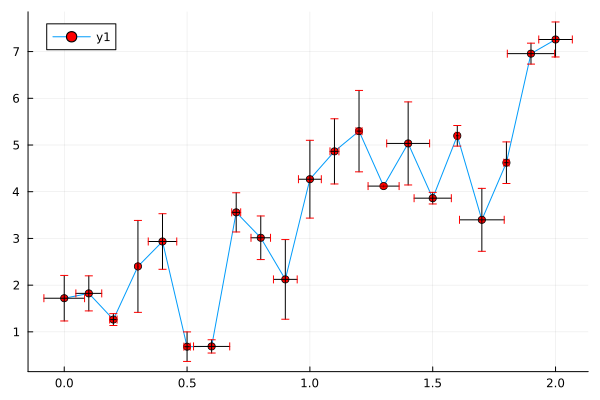
Graph with confidence intervals (arguments xerr and yerr)

In [ ]: 
using Random
Random.seed!(2018)

f(x) = 2 * x + 1
x = 0:0.1:2
n = length(x)
y = f.(x) + randn(n)

plot( x, y,
      xerr = 0.1 * rand(n),
      yerr = rand(n),
      marker = (:circle, :red) )
Out[0]:

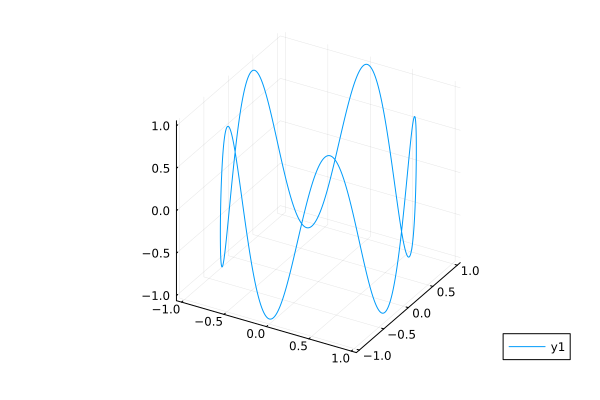
Three-dimensional graph

In [ ]: 
t = 0:pi/100:10pi;
x1 = sin.(1 * t)
y1 = cos.(1 * t)

x2 = sin.(2 * t)
y2 = cos.(2 * t)

plot(
    plot( x1, y1, t, leg=false, lw=2 ),
    plot( x2, y2, t, leg=false, lw=2 )
)
Out[0]:

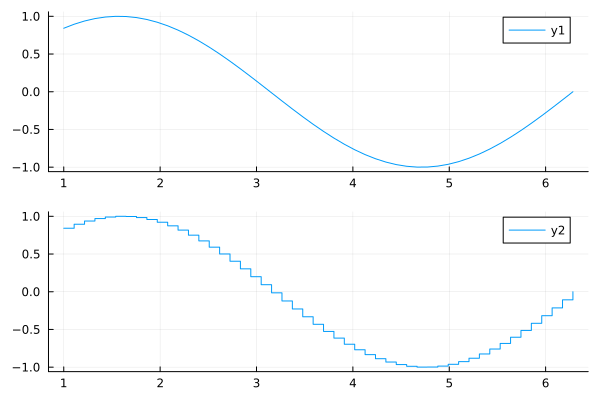
Smooth and stepwise graphs combined using an argument layout

In [ ]: 
x = range( 1, 2pi, length=50 )

plot( x, [sin.(x) sin.(x)],
      seriestype=[:line :step],
      layout = (2, 1) )
Out[0]:

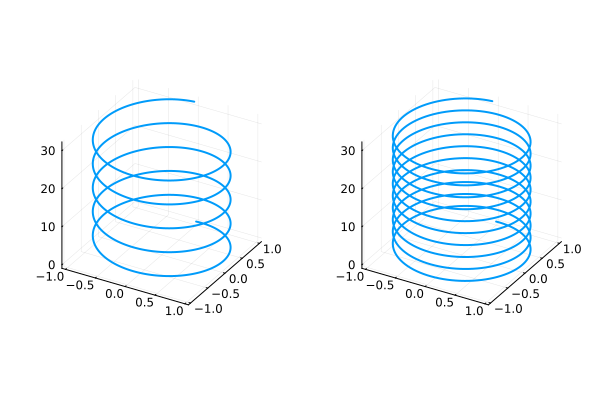
Parametric graph in 3D

In [ ]: 
t = range(0, stop=10, length=1000)

x = cos.(t)
y = sin.(t)
z = sin.(5t)

plot( x, y, z )
Out[0]:

Graphs in polar coordinates

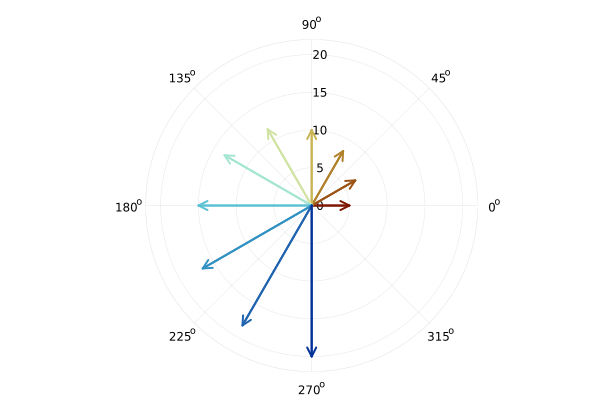
Arrows to the points forming the spiral (graph quiver)

In [ ]: 
cur_colors = theme_palette(:roma);
th = range( 0, 3*pi/2, 10 );
r = range( 5, 20, 10 );
c = collect(1:10)

X = r .* cos.(th)
Y = r .* sin.(th)

quiver( r.*0, r.*0, quiver=(th,r), aspect_ratio=:equal, proj=:polar,
        line_z=repeat(c, inner=4), c=:roma, cbar=false, lw=2 )
Out[0]:

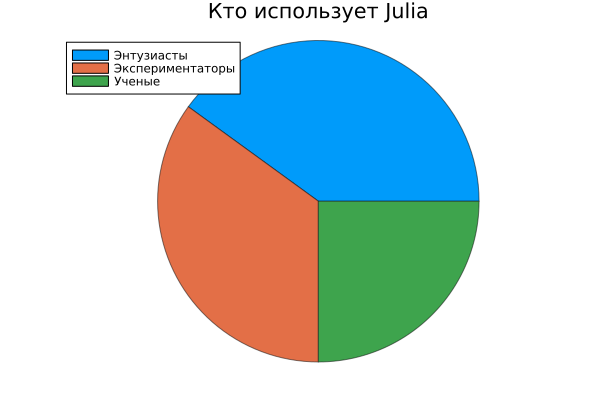
Function pie

In [ ]: 
x = [ "Enthusiasts", "The experimenters", "Scientists" ]
y = [0.4,0.35,0.25]

pie(x, y, title="Who uses Julia",l = 0.5)
Out[0]:

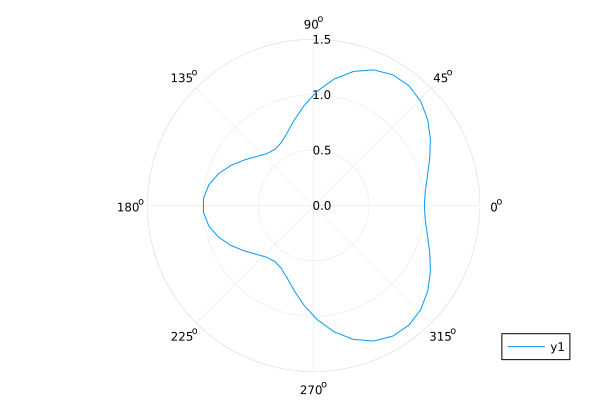
Function polar

In [ ]: 
θ = range(0, 2π, length=50)
r = 1 .+ cos.(θ) .* sin.(θ).^2

plot(θ, r, proj=:polar, lims=(0,1.5))
Out[0]:

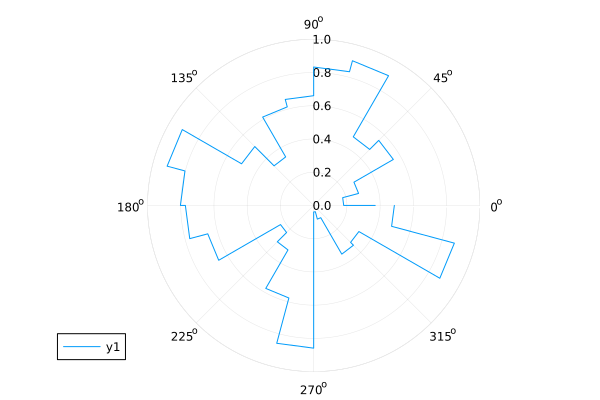
Stepwise graph in polar coordinates (graph rose)

In [ ]: 
using Random
Random.seed!(2018)

n = 24
R = rand(n+1)
θ = 0:2pi/n:2pi
plot( θ, R, proj=:polar, line=:steppre, lims=(0,1) )
Out[0]:

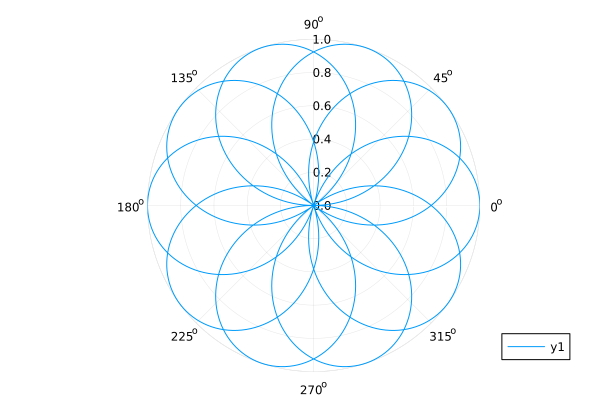
The graph in polar coordinates, set using the function

In [ ]: 
θ = range( 0, 8π, length=1000 )
fr(θ) = sin( 5/4 * θ )

plot( θ, fr.(θ), proj=:polar, lims=(0,1) )
Out[0]:

Bubble chart in polar coordinates

In [ ]: 
include( "$(@__DIR__)/data/planetData.jl" );

scatter( angle, distance, ms=diameter, mc = c,
         proj=:polar, legend=false,
         markerstrokewidth=1, markeralpha=.7 )
title!( "Planets of the Solar system" )
Out[0]:

Discrete data

Horizontally positioned bar chart (function bar)

In [ ]: 
ticklabel = string.( collect('but':'m') )
bar( 1:12, orientation=:h, yticks=(1:12, ticklabel), yflip=true )
Out[0]:

Bar charts bar and groupedbar

In [ ]: 
using StatsPlots
include( "$(@__DIR__)/data/BostonTemp.jl" );

plots_id = [1,2,3];

groupedbar( hcat([Temperatures[i,:] for i in plots_id]...),
            xticks=(1:12, Months),
            label = [Years[i] for i in plots_id]',
            color = reshape(palette(:tab10)[1:3], (1,3)) )
Out[0]:

Chart stem (stvol-list)

In [ ]: 
x1 = range( 0, 2pi, 50 );
x2 = range( pi, 3pi, 50 );

X = [x1, x2];
Y = [cos.(x1), 0.5.*sin.(x2)];

plot( X, Y, line=:stem, marker=:circle )
Out[0]:

Three-dimensional stem-diagram

In [ ]: 
X = repeat( range(0,1,10), outer = [1,10] )
Y = repeat( range(0,1,10)', outer = [10,1] )

Z = exp.(X.+Y)

plot( X, Y, Z, line=:stem, color=:skyblue, markercolor=:white, marker=:circle, leg=false )
Out[0]:

Contour graphs

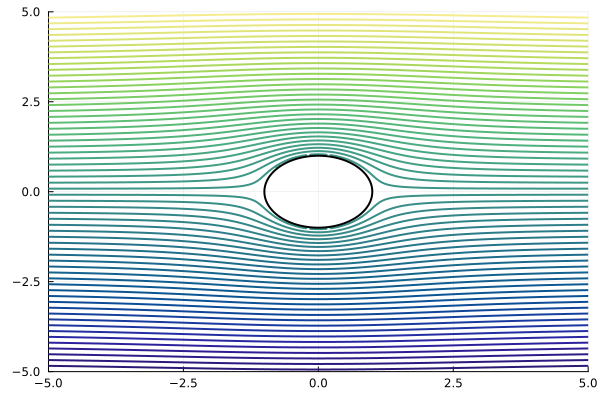
Graph of laminar flow around a cylinder.

Analytical approximation of this function is calculated using the equation:

In [ ]: 
include( "$(@__DIR__)/data/flowAroundCylinder.jl" );

(r, theta, x, y, streamline, pressure) = flowAroundCylinder();

plot( x, y, streamline, levels=60, seriestype=:contour,
      xlim = [-5,5], ylim=[-5,5], cbar=false, linewidth=2,
      leg=false, color=:haline )

(xx,yy) = circle( 0, 0, 1 );

plot!( xx, yy, lw=2, lc=:black )
Out[0]:

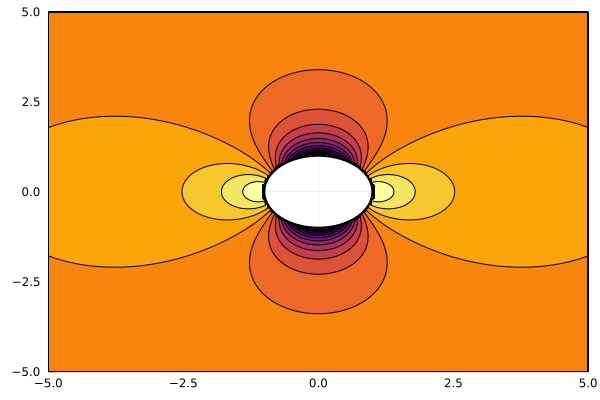
Filled contour graph (static pressure around a cylinder streamlined by a laminar flow)

In [ ]: 
include( "$(@__DIR__)/data/flowAroundCylinder.jl" );

(r, theta, x, y, streamline, pressure) = flowAroundCylinder();
plot( x, y, pressure, seriestype=:contourf, xlim = [-5,5], ylim=[-5,5], cbar=false, linewidth=1, leg=false )

(xx,yy) = circle( 0, 0, 1 );
plot!( xx, yy, lw=2, lc=:black )
Out[0]:

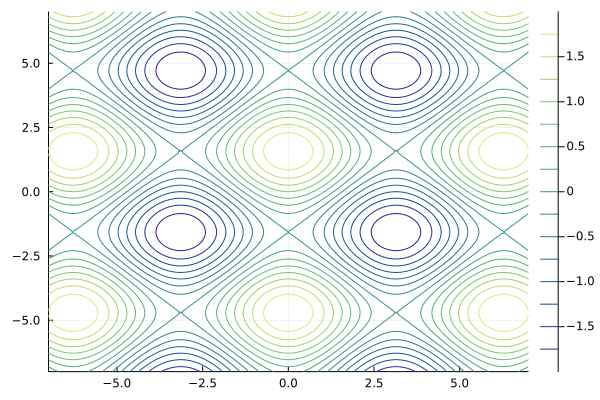
Contour graph of mathematical functions

In [ ]: 
# Prepare the data
y = x = range( -7, 7, step=0.1 )
z = @. sin(x) + cos(y')

Plots.contour( x, y, z, color=:haline )
Out[0]:

Surfaces and grids

Parameter seriestype=:surface

In [ ]: 
# Prepare the data
y = x = range( -7, 7, step=0.1 )
z = @. sin(x) + cos(y')

plot( x, y, z, st=:surface, color=:cool )
Out[0]:

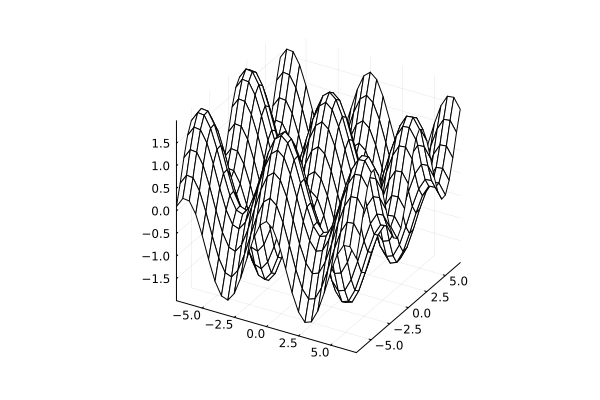
Parameter seriestype=:wireframe

In [ ]: 
# Prepare the data
y = x = range( -7, 7, step=0.5 )
z = @. sin(x) + cos(y')

plot( x, y, z, st=:wireframe )
Out[0]:

Graph of a two-dimensional function

In [ ]: 
include( "$(@__DIR__)/data/peaks.jl" );

(x,y,z) = peaks();

plot( x, y, z; levels=20, st=:surface )
Out[0]:

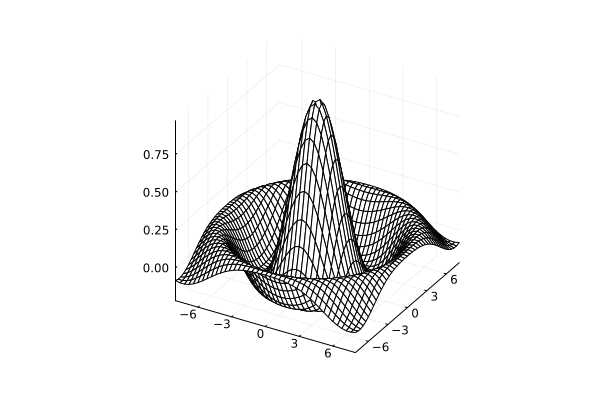
Let's plot the graph of the "sombrero" function. When using gr() argument hidesurface not used. But when using plotly() argument hidesurface=false allows you to simultaneously display both the surface and the contour graph on it.

In [ ]: 
x = y = range( -8, 8, length=41 )
f(x,y) = sin.(sqrt.(x.*x+y.*y))./sqrt.(x.*x+y.*y)

# in gr(), this method allows you to see the graph of the surface behind the graph of the lines.
p = plot( x, y, f, st=:surface, fillalpha=0.7, cbar=false ) 
plot!( p, x, y, f, st=:wireframe )

# plotly() has a more convenient syntax.
# wireframe( x, y, f, hidesurface=false )
Out[0]:

A surface graph combined with a contour graph

In [ ]: 
Pkg.add("Contour")
In [ ]: 
using Contour

# Data
x = range(-3, 3, length=50)
y = range(-3, 3, length=50)
# z = [exp(-(xi^2 + yi^2)/5) * sin(xi^2 + yi^2) for xi in x, yi in y]
z = sin.(2*x) .+ cos.(1.6y')

colors = cgrad(:viridis, 8) # A palette of graphics divided into 10 colors
levels = range(minimum(z), maximum(z), length=10)[2:9] # 8 levels (from 2nd to 9th out of 10)
contour_data = Contour.contours(x, y, z, levels)  # Contours with preset levels (many lines in each)

# Creating a 3D graph
surface(x, y, z, c=:viridis, legend=false)  # 3D surface

# Contour graph on the XY plane
for cl in Contour.levels(contour_data)
    lvl = level(cl) # the Z value of the contour
    for line in lines(cl)
        ys, xs = coordinates(line) # coordinates of the points of the current contour segment
        plot!(xs, ys, zeros(size(xs)) .+ abs(1.1*minimum(z)), c=colors[lvl], lw=2)
    end
end

plot!()
Out[0]:

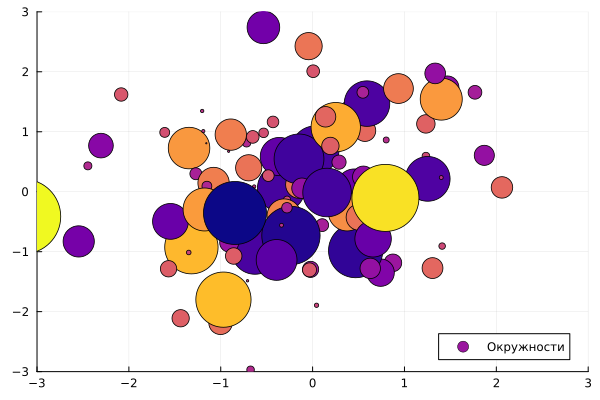
Dot charts and bubble charts

Bubble Chart

In [ ]: 
using Random: seed!
seed!(28)

xyz = randn(100, 3)

scatter( xyz[:, 1], xyz[:, 2], marker_z=xyz[:, 3],
         label="Circles",
         colormap=:plasma, cbar=false,
         markersize=15 * abs.(xyz[:, 3]),
         xlimits=[-3,3], ylimits=[-3,3]
       )
Out[0]:

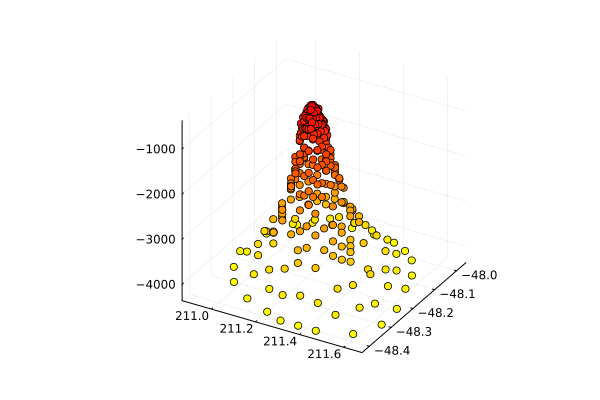
A three-dimensional dot graph with a separate color assigned to each point

In [ ]: 
using Colors, ColorSchemes
cs = ColorScheme([colorant"yellow", colorant"red"])
Out[0]:
No description has been provided for this image
In [ ]: 
using CSV, DataFrames

df = DataFrame(CSV.File( "$(@__DIR__)/data/seamount.csv" ))
C = get( cs, df.z, :extrema )

scatter( df.x, df.y, df.z, c=C, leg=false )
Out[0]:

A three-dimensional dot graph with a fictitious space for a color histogram

In [ ]: 
using CSV, DataFrames

df = DataFrame(CSV.File( "$(@__DIR__)/data/seamount.csv" ))
cs = cgrad(:thermal)
C = get( cs, df.x, :extrema )

l = @layout [a{0.97w} b]
p1 = scatter( df.x, df.y, df.z, c=C, leg=false )
p2 = heatmap(rand(2,2), clims=(0,10), framestyle=:none, c=cgrad(cs), cbar=true, lims=(-1,0))
plot(p1, p2, layout=l)
Out[0]:

Color and annotations

Creating a color palette:

In [ ]: 
using Images
scheme = rand(RGB, 10)
Out[0]:
No description has been provided for this image

We use the palette to color the matrix from random numbers and output it as an image.:

In [ ]: 
matrix = rand(1:10, 20, 20)
img = scheme[ matrix ]
Out[0]:
No description has been provided for this image

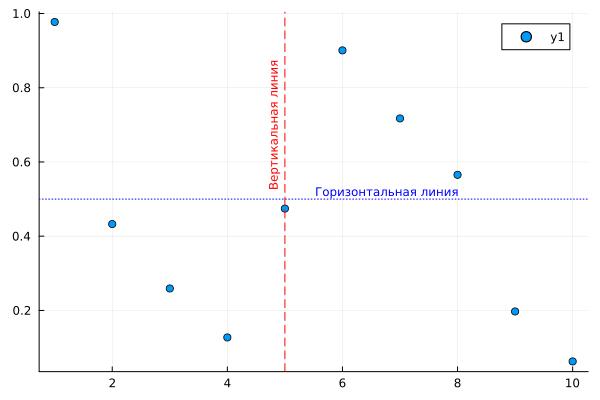
Let's create a graph from random points with lines and annotations.:

In [ ]: 
x = 1:10
y = rand(10)

# Creating a dot graph
scatter(x, y)

# Let's draw vertical and horizontal lines on the graph
vline!( [5], color=:red, linestyle=:dash, label=:none )
hline!( [0.5], color=:blue, linestyle=:dot, label=:none )

# Let's put annotations on the graph (it only works in gr())
annotate!( 8, 0.52, text("Horizontal line", :blue, :right, 8))
annotate!( 4.8, 0.7, text("Vertical line", :red, 8, rotation = 90))
Out[0]: