Data Approximation (Engee application)

We present a toolkit for developing our own applications using the example of the Data Approximation tool.

The purpose of this application is

The Data Approximation tool is designed to help you find good functions for approximating input data vectors.

The purpose of this particular example is to show and discuss application development techniques in Engee using GenieFramework.

Launching the app

In the folder with this example you will find the file app.jl, which we will launch as a separate application in Engee with the following commands:

genie_app = engee.genie.start("$(@__DIR__)/app.jl", log_file="log.txt");

The application can be opened in a separate window.:

display("text/html", """<a href="$(string(genie_app.url))" target="_blank">Открыть в отдельном окне</a>""")

Or it can be displayed inside an interactive script.:

display(MIME("text/html"), """<iframe src="$(string(genie_app.url))" width="1100" height="680" style="border: none;"></iframe>""";)

Stopping the application (for debugging or restarting)

To stop the application, run the following command, uncomenting it:

# engee.genie.stop("$(@__DIR__)/app.jl"));

Creating input vectors

Let's create the input data that will be required for the application to work.:

# Полиномиальная функция
v1 = 1:5
v2 = (v1.^3 .+ 3v1 .- 5)./150;

# Экспонента
v3 = 3 .* exp.(v1 .- 4);

# Обычная логистическая регрессия
n = 1000
xr = randn(n)
yr = Float32.((1.0 ./ (1.0 .+ exp.(-xr))) .> rand(n))

# Ступенчатая функция (тоже для логистической регрессии)
yr1 = Float32.(xr .> (minimum(xr) + 0.5*abs(maximum(xr)-minimum(xr))))

# Гауссова функция (единичная - осторожно, это всё еще линейная регрессия)
normal_pdf(x; μ=0, σ=1) = exp(-(x-μ)^2/(2σ^2)) / (σ * sqrt(2π))
xn = collect(-3:0.1:3);
yn = normal_pdf.(xn);
yn1 = normal_pdf.(xn, μ=1, σ=0.001);

Plotting the found function

The found functions can be copied from a line in the application and pasted into an interactive script cell to get the output data.:

f(x) = 1/(1+exp(-(3.99922 + 8.62808 * x)))

plot(-4:0.1:4, f, lw=3, leg=false)
scatter!(xr,yr1)

How does it work?

Here is a small demo with the test vectors above:

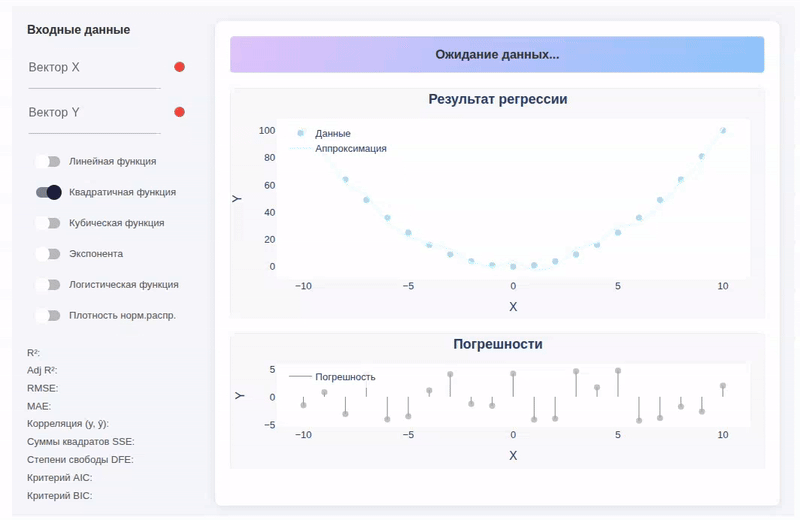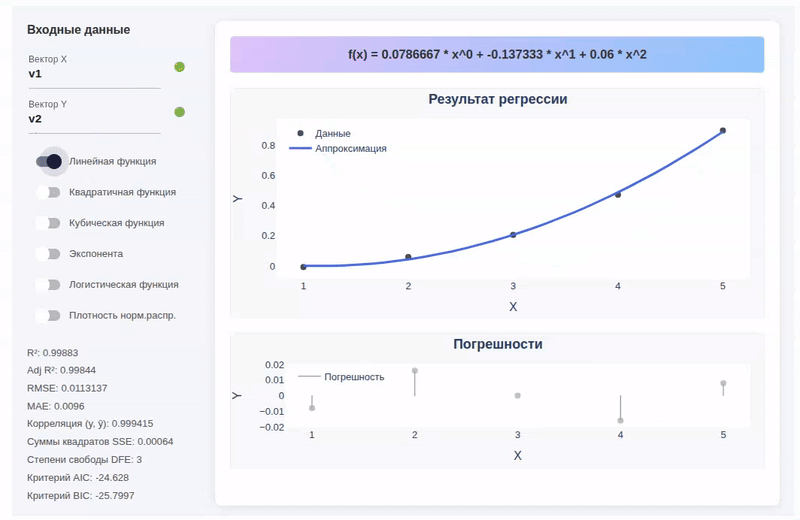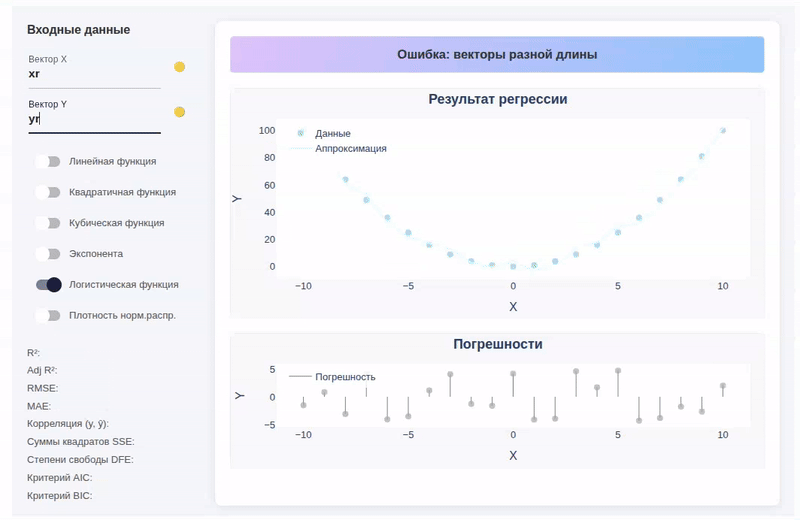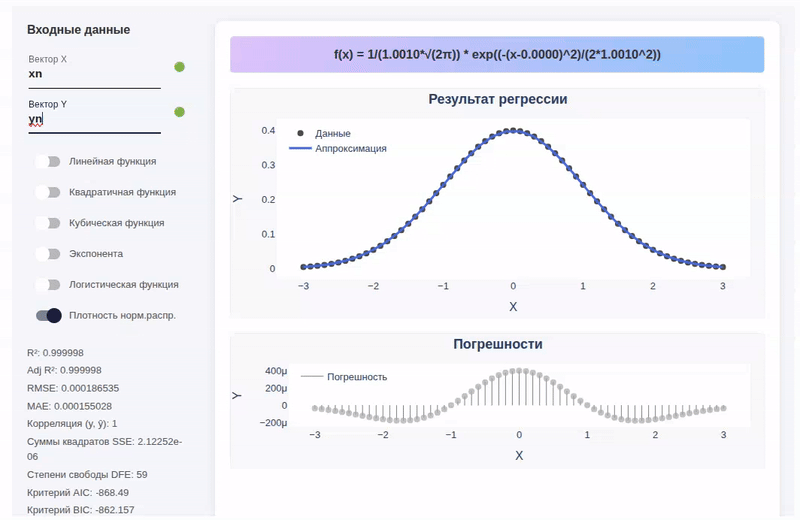
Comments about the program's operation

Any data that is added to the vectors inside the tool via a function call can be used as input vectors. collect().

Part of the regression tasks is performed using the method of named squares, and part is performed using gradient descent with a moment. This gives some confidence in the convergence of the regression, but due to the limited number of iterative algorithm steps, the best approximation may not be achievable for some datasets. It is worth increasing the number of steps in the tool code.

If you go into the code of the tool, you will see a fairly standard application structure.:

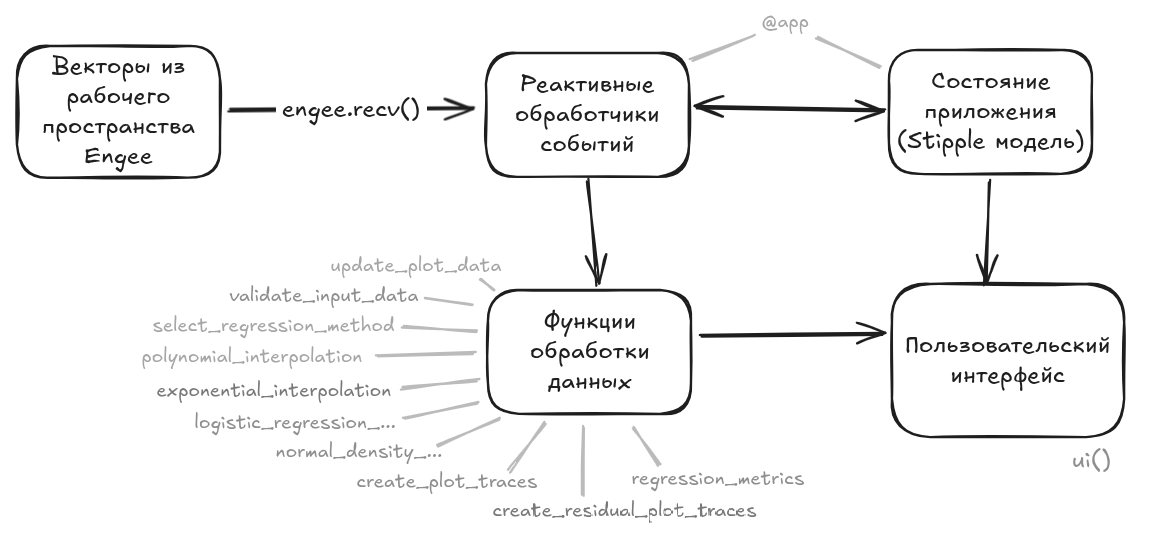
Conclusion

We hope for your feedback to make the tool more useful and eliminate errors.