Engee documentation
Notebook

OFDM oversampled signal model

In this example we will look at an oversampled OFDM (Orthogonal frequency-division multiplexing, a digital modulation technique using a large number of closely spaced orthogonal subcarriers, or multiplexing) signal model. The model allows you to see the coupling of multiple modulations. Another example uses an RMS unit that measures an OFDM modulated signal with noise superimposed on it, scaled by a value proportional to the number of active subcarriers relative to the size of the FFT (Fast Fourier transform) to confirm that the signal power is approximately equal to one.

The model is constructed according to the following principle.

  1. A random integer data set and pilot input symbols are generated.
  2. 16-QAM modulates the data and pilot symbols.
  3. OFDM modulates the QAM modulated signal. A pair of OFDM modulators and demodulators process three symbols with different pilot signal subcarrier indices and cyclic prefix lengths for each symbol. The OFDM signal contains data and pilots, which the model generates at four times the sampling rate.
  4. Next, we apply aplitude distortion to each frame, which significantly changes the signal power.
  5. OFDM then demodulates and outputs the data and pilots separately.
  6. 16-QAM demodulates the data and pilot symbols.
  7. After that find the difference between input and output.

The figure below shows the implemented model.

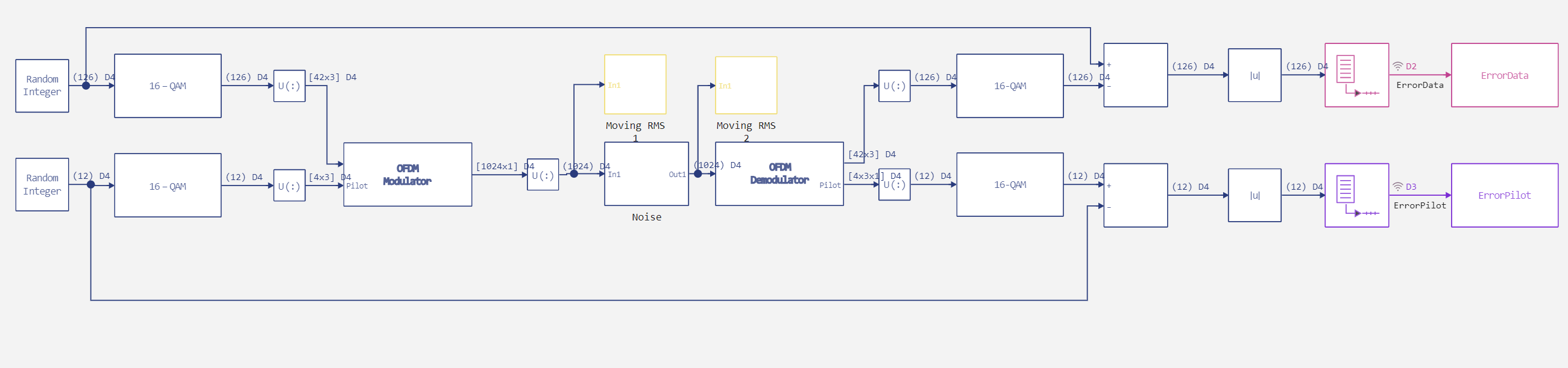
image.png

Let's initialise the parameters of the model.

In [ ]: 
M = 16;              # Порядок модуляции
nfft = 64;           # Длина FFT
NumSymbols=3;        # Количество символов OFDM
osf=4;               # Фактор передискретизации
ngbc = [9;8];        # Число носителей защитного диапазона
insertdcnull = true;  # Наличие DC-нулевой поднесущей
addpilotport = true;  # Присутствие пилота
Noise_power = 10; # Мощность шума
In [ ]: 
# Индексы пилотных поднесущих
pscindx = [[12;26;40;54] [14;28;38;52] [12;26;40;54]]; 
cplen = [16; 32; 16];  # CyclicPrefixLength
# Выборки на кадр для данных
spf_data = NumSymbols * (nfft-sum(ngbc)-size(pscindx,1)-insertdcnull)
# Выборки на кадр для пилота    
spf_pilot = NumSymbols * size(pscindx,1)
# Число активных поднесущих
nasc = nfft-sum(ngbc)+insertdcnull;

After declaring the model parameters, let's initialise the model start function and start the model itself.

In [ ]: 
# Подключение вспомогательной функции запуска модели.
function run_model( name_model)
    
    Path = (@__DIR__) * "/" * name_model * ".engee"
    
    if name_model in [m.name for m in engee.get_all_models()] # Проверка условия загрузки модели в ядро
        model = engee.open( name_model ) # Открыть модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
    else
        model = engee.load( Path, force=true ) # Загрузить модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
        engee.close( name_model, force=true ); # Закрыть модель
    end
    sleep(5)
    return model_output
end

run_model("OFDM_Signal_and_QAM") # Запуск модели.

Building...
Progress 0%
Progress 0%
Progress 0%
Progress 3%
Progress 8%
Progress 13%
Progress 18%
Progress 23%
Progress 28%
Progress 33%
Progress 38%
Progress 43%
Progress 48%
Progress 54%
Progress 59%
Progress 64%
Progress 69%
Progress 74%
Progress 79%
Progress 84%
Progress 89%
Progress 94%
Progress 99%
Progress 100%
Progress 100%
Out[0]:
Dict{String, DataFrame} with 4 entries:
  "ErrorPilot" => 121×2 DataFrame…
  "RMSout"     => 10241×2 DataFrame…
  "ErrorData"  => 1261×2 DataFrame…
  "RMSinp"     => 10241×2 DataFrame…

Now let's analyse the recorded data.

In [ ]: 
ErrorData = collect(ErrorData);
ErrorPilot = collect(ErrorPilot);
RMSinp = collect(RMSinp);
RMSout = collect(RMSout);

ErrorData = ErrorData.value;
ErrorPilot = ErrorPilot.value;
RMSinp = RMSinp.value;
RMSout = RMSout.value;
In [ ]: 
plot([real(RMSinp),real(RMSout)], title="RMS", label=["До наложения шума" "После наложения шума"])
Out[0]:

As we can see, the signal power varies from frame to frame. Now let's look at the difference between input and output data.

In [ ]: 
plot([ErrorData,ErrorPilot], title="Разница между входами и выходами", label=["Данные" "Пилоты"])
Out[0]:

Judging by the graph, the error is zero, but to be sure, let's find the total error.

In [ ]: 
println("Суммарная разница между входными и выходными данными: " * string(sum(ErrorData)))
println("Суммарная разница между входными и выходными пилотами: " * string(sum(ErrorPilot)))

Суммарная разница между входными и выходными данными: 0.0
Суммарная разница между входными и выходными пилотами: 0.0

Conclusion

In this example we have broken down and demonstrated the possibilities of using several types of modulation in communication systems. This approach is very much in demand in this field of activity.

Blocks used in example