Calculation of BER for QPSK

The Error Rate Calculation block calculates the error rate by bits (bit error rate, BER). Using this block, we can obtain BER data for the communication system and analyze the effectiveness of our system. In this example, we will look at a simple QPSK receiver and transmitter model. It is shown in the picture below.

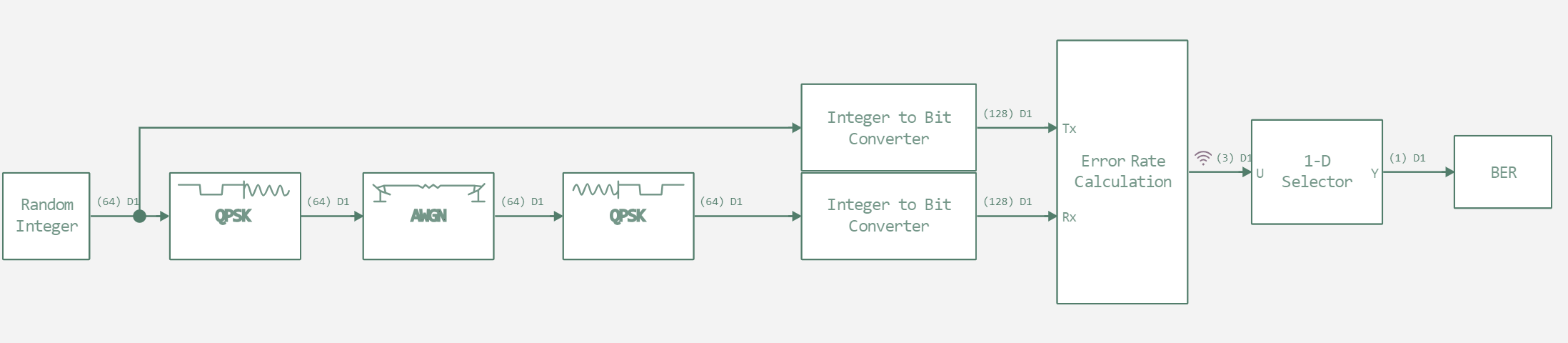
Next, we will set an auxiliary function to run the model.

# Подключение вспомогательной функции запуска модели.
function run_model( name_model)
    
    Path = (@__DIR__) * "/" * name_model * ".engee"
    
    if name_model in [m.name for m in engee.get_all_models()] # Проверка условия загрузки модели в ядро
        model = engee.open( name_model ) # Открыть модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
    else
        model = engee.load( Path, force=true ) # Загрузить модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
        engee.close( name_model, force=true ); # Закрыть модель
    end
    sleep(5)
    return model_output
end

run_model (generic function with 1 method)

Next, we will initialize the signal-to-noise ratio indicators for our model and declare a bit error variable.

EbNoArr = collect(-9:3:9);
Eb_No = 0;
ber = zeros(length(EbNoArr));
BER = 0;

Now let's run the model at different values of the signal-to-noise ratio.

for i in 1:length(EbNoArr)
    Eb_No = EbNoArr[i]
    run_model("QPSK") # Запуск модели.
    BER = collect(BER)
    ber[i]=BER.value[end][1]
    println("BER: $(ber[i])")
end

Building...
Progress 0%
Progress 38%
Progress 100%
BER: 0.3271484375
Building...
Progress 0%
Progress 28%
Progress 100%
BER: 0.25244140625
Building...
Progress 0%
Progress 32%
Progress 100%
BER: 0.1611328125
Building...
Progress 0%
Progress 76%
Progress 100%
BER: 0.07275390625
Building...
Progress 0%
Progress 44%
Progress 100%
BER: 0.01904296875
Building...
Progress 0%
Progress 57%
Progress 100%
BER: 0.00244140625
Building...
Progress 0%
Progress 57%
Progress 100%
BER: 0.0

Let's plot the BER graph.

using SpecialFunctions
function berawgn_psk(EbNo_dB, M)
    EbNo = 10 .^ (EbNo_dB ./ 10)
    if M == 2
        return 0.5 .* erfc.(sqrt.(EbNo))# аналогично для QPSK с Gray-кодированием
    else
        k = log2(M)
        return 2 * erfc.(sqrt.(k .* EbNo) .* sin(π/M)) / k
    end
end
ber_ref = berawgn_psk(EbNoArr, 2)
println("__Eb_No__: $EbNoArr")
println("_ber_ref_: $(round.(ber_ref, digits=3))")
println("ber_model: $(round.(ber, digits=3))")

p1 = plot(EbNoArr, ber_ref, seriestype = :scatter, marker = :rect, label = "Theoretical QPSK", yscale = :log10)
plot!(p1, EbNoArr, ber, seriestype = :scatter, marker = :diamond, label = "Model QPSK")
xlabel!(p1, "Eb/No (dB)")
ylabel!(p1, "BER")
title!(p1, "Bit Error Rate (Log Scale)")
# Второй график: обычный масштаб
p2 = plot(EbNoArr, ber_ref, seriestype = :scatter, marker = :rect, label = "")
plot!(p2, EbNoArr, ber, seriestype = :scatter, marker = :diamond, label = "")
ylabel!(p2, "BER")
title!(p2, "Bit Error Rate (Linear Scale)")

# Общий вывод: два графика рядом
plot(p2, p1, layout = (2, 1), size=(1000,400))

__Eb_No__: [-9, -6, -3, 0, 3, 6, 9]
_ber_ref_: [0.308, 0.239, 0.158, 0.079, 0.023, 0.002, 0.0]
ber_model: [0.327, 0.252, 0.161, 0.073, 0.019, 0.002, 0.0]

Conclusion

As you can see in this example, the higher the signal-to-noise ratio, the lower the error.
Here we have figured out how to build a BER graph for a simple communication system model and learned how to apply this method to analyze the system.

Calculation of BER for QPSK

Conclusion

Blocks used in example¶