Engee documentation
Notebook

The encryption model using a substitution-permutation network (SP-network)

We study the principles of organizing a modern encryption system using a theoretical example.

Task description

Most modern information systems use the AES cipher (or similar) to encrypt messages. These ciphers are based on the algorithm of the substitution-permutation network (SP-network).

If you just need to encrypt or decrypt a message, Julia has libraries like AES.jl, allowing you to encrypt and decrypt byte sequences.

The algorithm presented here is not necessarily a reliable cipher. This cipher can make the right choice of S- and P-block parameters, as well as the best functions for generating round keys and adding them to the ciphertext, and there are other additional mechanisms described in the standards. We are only creating a training example, which in some respects is convenient to analyze and refine.

General view of the model

An SP-network-based cipher receives a block of data and a key as input and performs several rounds consisting of alternating stages of substitution and permutation of bits in the block.

image.png
In [ ]: 
# Загрузим модель, если она еще не открыта на холсте
if "sp_net_cipher_model" ∉ getfield.(engee.get_all_models(), :name)
    engee.load( "$(@__DIR__)/sp_net_cipher_model.engee");
end

model_data = engee.run( "sp_net_cipher_model" );

println( "Количество ошибок передачи: ", convert(Int, model_data["Кол-во ошибок"].value[end]) )

Количество ошибок передачи: 0

Next, we will expand each block of the model and see how one separate round works.

A model with three rounds of encryption

If you open each of the subsystems, you can get a very visual representation of the work of each round of the algorithm (model sp_net_cipher_model_3R_expand).

It allows you to see the settings of each stage and check what happens if the settings of the wildcard or permutation blocks are not consistent.

image.png

Let's run this model and check that the message is being transmitted with the same bytes. AAAAAAAA generates different bytes of ciphertext:

In [ ]: 
# Загрузим модель, если она еще не открыта на холсте
if "sp_net_cipher_model_3R_expand" ∉ getfield.(engee.get_all_models(), :name)
    engee.load( "$(@__DIR__)/sp_net_cipher_model_3R_expand.engee");
end

model_data = engee.run( "sp_net_cipher_model_3R_expand" );

source_message = collect(model_data["Блок сообщения"]).value
cipher_text = UInt16.(collect(model_data["Зашифрованный блок"]).value)
received_message = UInt16.(collect(model_data["Расшифрованный блок"]).value)

source_bytes = vcat( reverse.([reinterpret( UInt8, [UInt16(c)]) for c in source_message])... )
cipher_bytes = vcat( reverse.([reinterpret( UInt8, [UInt16(c)]) for c in cipher_text])... )
received_bytes = vcat( reverse.([reinterpret( UInt8, [UInt16(c)]) for c in received_message])... )

println( "Отправленное сообщение: ", join( vcat( string.(source_bytes, base=16)... ), " " ) )
println( "Зашифрованное сообщение: ", join( vcat( string.(cipher_bytes, base=16)... ), " " ))
println( "Полученное сообщение: ", join( vcat( string.(received_bytes, base=16)... ), " " ) )

Отправленное сообщение: 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41
Зашифрованное сообщение: 3f 73 25 f1 71 65 64 39 d0 4d 3f 96 b2 eb e1 24 3f 73 25 f1 71 65 64 39 d0 4d 3f 96 b2 eb e1 24 3f 73 25 f1 71 65 64 39 d0 4d
Полученное сообщение: 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41
In [ ]: 
println( "Отправленная строка: ", String( source_bytes ))
println( "Полученная строка: ", String( received_bytes ))

Note that the ciphertext started repeating itself starting from block 17.

The one-round cipher model

If we simplify the network to a single round, the model will look like this:

image.png

We see all the usual elements of the SP network.:

  • the function of mixing key bits with plaintext bits (XOR),
  • substitution blocks that accept bit values (Bool) input vectors,
  • bit permutation blocks, which accepts as input a vector of four combined results of the previous operation.

If all the parameters of the S- and P-blocks are set correctly, then we get the same message at the output as it was at the input.

In [ ]: 
# Загрузим модель, если она еще не открыта на холсте
if "sp_net_cipher_model_1R" ∉ getfield.(engee.get_all_models(), :name)
    engee.load( "$(@__DIR__)/sp_net_cipher_model_1R.engee");
end

model_data = engee.run( "sp_net_cipher_model_1R" );

Let's examine the sent and received message.:

In [ ]: 
source_message = collect(model_data["Блок сообщения"]).value
cipher_text = UInt16.(collect(model_data["Зашифрованный блок"]).value)
received_message = UInt16.(collect(model_data["Расшифрованный блок"]).value)

source_bytes = vcat( reverse.([reinterpret( UInt8, [UInt16(c)]) for c in source_message])... )
cipher_bytes = vcat( reverse.([reinterpret( UInt8, [UInt16(c)]) for c in cipher_text])... )
received_bytes = vcat( reverse.([reinterpret( UInt8, [UInt16(c)]) for c in received_message])... )

println( "Отправленное сообщение: ", join( vcat( string.(source_bytes, base=16)... ), " " ) )
println( "Зашифрованное сообщение: ", join( vcat( string.(cipher_bytes, base=16)... ), " " ))
println( "Полученное сообщение: ", join( vcat( string.(received_bytes, base=16)... ), " " ) )

Отправленное сообщение: d0 a1 d0 be d0 be d0 b1 d1 89 d0 b5 d0 bd d0 b8 d0 b5
Зашифрованное сообщение: 7c 9c e3 60 7e 1c f7 5a 6e 9c 6b f0 f8 cc ef b6 2c 5f
Полученное сообщение: d0 a1 d0 be d0 be d0 b1 d1 89 d0 b5 d0 bd d0 b8 d0 b5
In [ ]: 
println( "Отправленная строка: ", String( source_bytes ))
println( "Полученная строка: ", String( received_bytes ))

Отправленная строка: Сообщение
Полученная строка: Сообщение

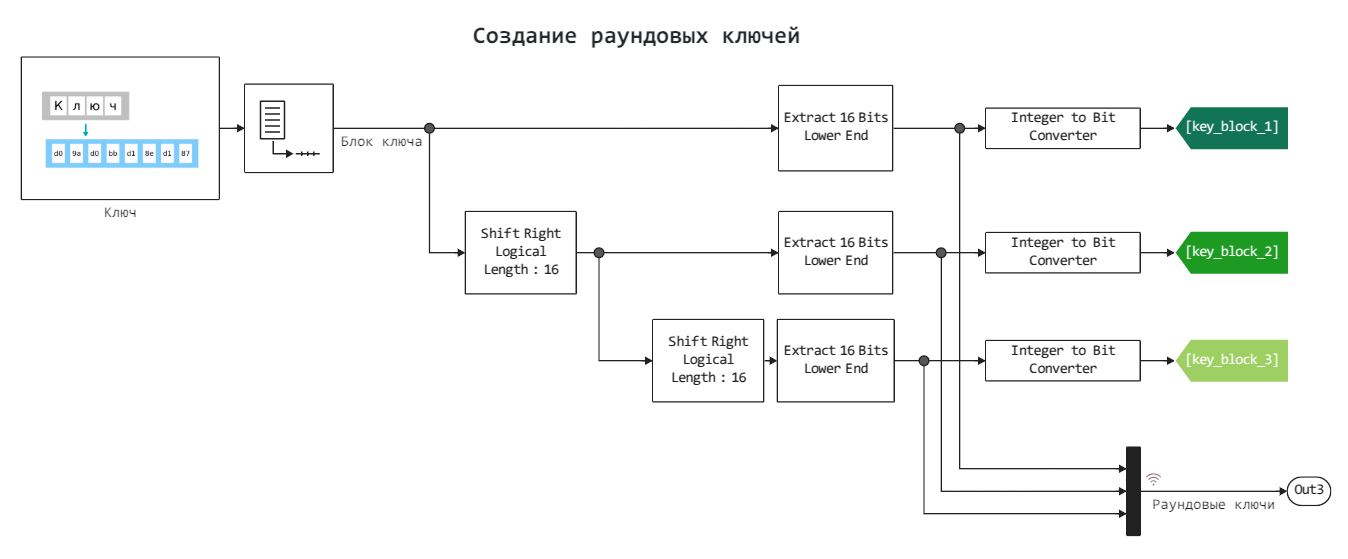
Creating round keys

The algorithm for creating round keys is organized as follows:

  • The byte sequence forming the key is divided into 64-bit blocks.
  • blocks overlap (key d0 9a d0 bb d1 8e d1 87 generates blocks d0 9a d0 bb, 9a d0 bb d1, d0 bb d1 8e etc.)
  • the key is used cyclically

The 64-bit key block is divided into 4 round keys of 16 bits each (sequentially), of which we use only the first three round keys.

image.png

Considerations for working with the model

When interpreting or planning model changes, the following features should be considered::

  • The message and key are passed to the model cyclically and never end.,
  • a full cycle of work with one unit is performed in one simulation cycle without delay
  • therefore, at the top level, we do not work with vectors of bits, but with numbers. UInt16, UInt32 etc.,
  • the input message and round keys are fed into the model in blocks of 16 bits, all four S-blocks at each round accept blocks of 4 bits as input, and P-blocks with vectors of 16 binary bits,
  • the permutation parameters inside the S- and P-blocks are not taken from the codebook, but are generated by the operation shuffle with the specified seed.
  • the message is transmitted to the algorithm in non-overlapping blocks, and the key blocks are generated by a window with an offset of one byte.

Conclusion

We have created a model that allows us to study all the stages of message encryption using the SP network and make any changes to the architecture of this algorithm without diving into technical programming issues.

Blocks used in example