Engee documentation
Notebook

The permutation cipher model

We implement a permutation cipher model that changes the bit order in the characters of the input message.

Task description

The permutation cipher that we are implementing will perform a bitwise permutation of each byte from the input message. If a symbol comes to the input 31 (00011111), then after applying the permutation table [2, 1, 5, 8, 4, 6, 7, 3] we will get an encrypted character. 62 (00111110).

A model describing this task is given below.:

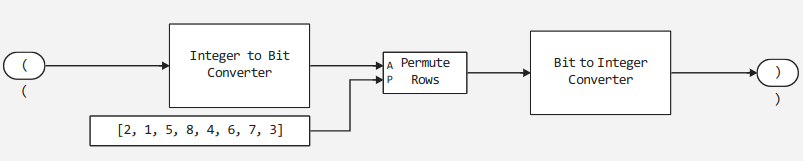
image.png

Hidden behind the permutation blocks are subsystems that carry out

  • decomposition of the input symbol into a bit array (block Integer to Bit Converter),
  • **permutation of ** bits using a block (block Permute Matrix),
  • forming the number UInt8 from a vector of bits (block Bit to Integer Converter).
image.png

The number on the front of the block indicates the set value for initializing the random number generator. When changing this value (field Seed block masks) the order of permutation inside the element is automatically overwritten to the one set by the function shuffle the order of permutation.

Launching the model and analyzing the results

In [ ]: 
# Загрузим модель, если она еще не открыта на холсте
if "permutation_cipher_model" ∉ getfield.(engee.get_all_models(), :name)
    engee.load( "$(@__DIR__)/permutation_cipher_model.engee");
end

model_data = engee.run( "permutation_cipher_model" );

Let's see what values passed through each of the communication lines during the simulation.:

In [ ]: 
source_message = collect(model_data["Сообщение"]).value
cipher_text = Int.(collect(model_data["Шифротекст"]).value)
received_message = Int.(collect(model_data["Расшифровка"]).value)

println( "Отправленное сообщение: ", source_message )
println( "Зашифрованное сообщение: ", cipher_text )
println( "Полученное сообщение: ", received_message )

Отправленное сообщение: [31, 12, 19, 17, 16, 15, 6, 15, 20, 1, 31, 12, 19, 17, 16, 15, 6, 15, 20, 1, 31]
Зашифрованное сообщение: [62, 36, 26, 24, 8, 54, 6, 54, 12, 16, 62, 36, 26, 24, 8, 54, 6, 54, 12, 16, 62]
Полученное сообщение: [31, 12, 19, 17, 16, 15, 6, 15, 20, 1, 31, 12, 19, 17, 16, 15, 6, 15, 20, 1, 31]

Decoding the message:

In [ ]: 
alphabet_dict = Dict( zip( 1:33, "абвгдеёжзиёклмнопрстуфхцчшщъыьэюя" ))
print( "Расшифрованное сообщение: ", join( [alphabet_dict[d] for d in received_message], "" ) )

Расшифрованное сообщение: экспонентаэкспонентаэ

Conclusion

We have created another basic block for building cryptographic systems – the simplest block for direct and "reverse" bit permutation inside message characters.

Blocks used in example