[医]三角帆
|
该页面正在翻译中。 |
#
<无翻译>*麦琪[医]三角帆*-Function
tricontourf(triangles::Triangulation, zs; kwargs...)
tricontourf(xs, ys, zs; kwargs...)绘制高度信息的填充三角图 zs 在水平位置 x 和垂直位置 ys. A 三角测量 来自DelaunayTriangulation。也可以提供jl代替 x 和 ys 用于指定三角形,否则为 x 和 ys 被计算。
绘图类型
绘图类型别名 [医]三角帆 功能是 [医]三角帆.
例子:
using CairoMakie
using Random
Random.seed!(1234)
x = randn(50)
y = randn(50)
z = -sqrt.(x .^ 2 .+ y .^ 2) .+ 0.1 .* randn.()
f, ax, tr = tricontourf(x, y, z)
scatter!(x, y, color = z, strokewidth = 1, strokecolor = :black)
Colorbar(f[1, 2], tr)
f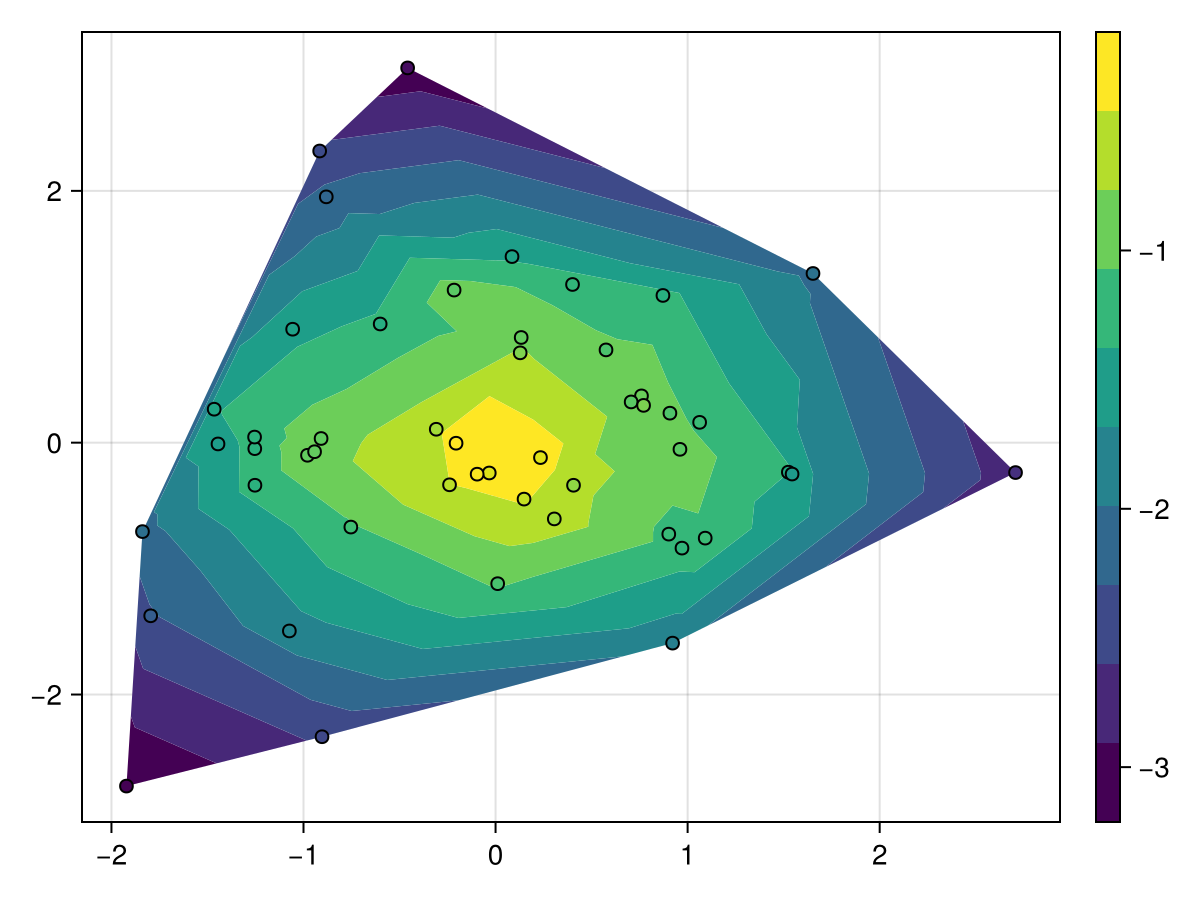
using CairoMakie
using Random
Random.seed!(1234)
x = randn(200)
y = randn(200)
z = x .* y
f, ax, tr = tricontourf(x, y, z, colormap = :batlow)
scatter!(x, y, color = z, colormap = :batlow, strokewidth = 1, strokecolor = :black)
Colorbar(f[1, 2], tr)
f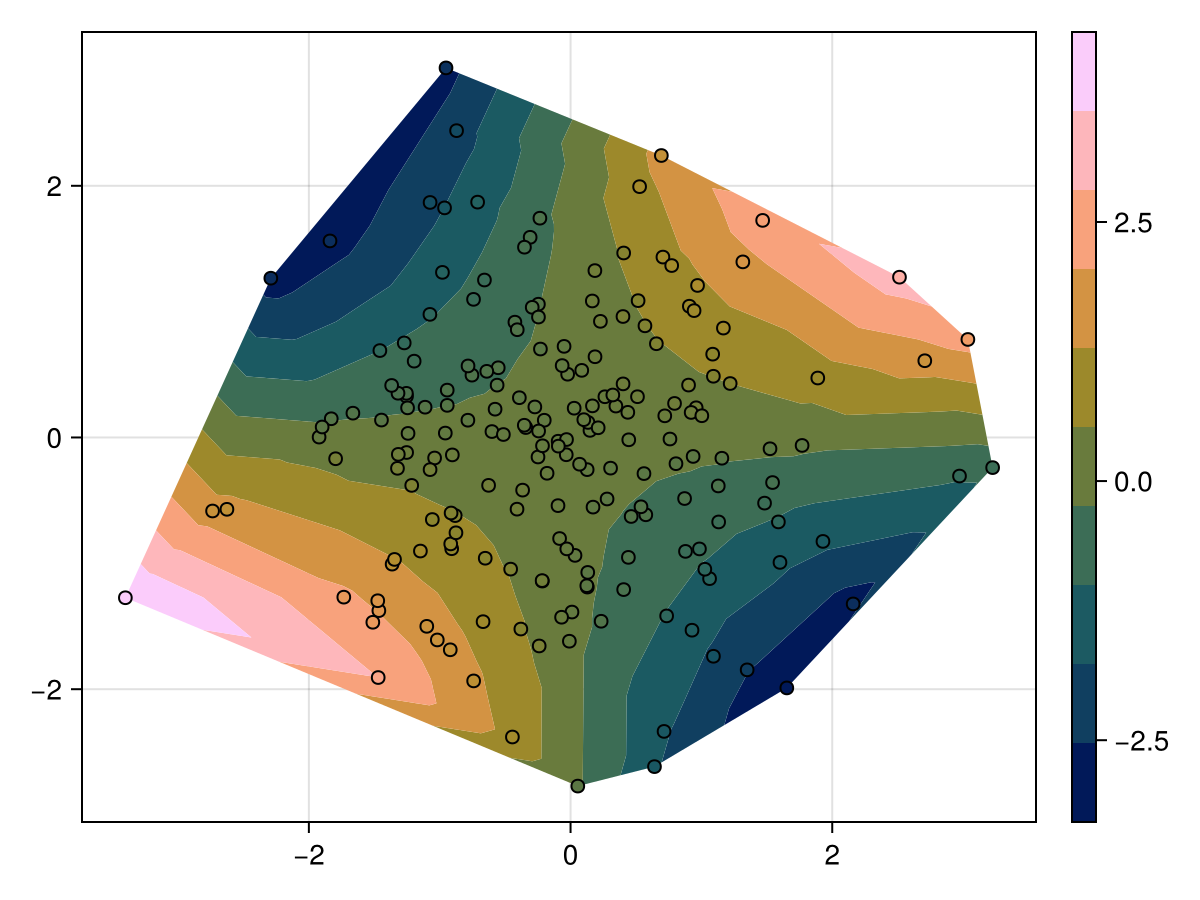
三角测量模式
using CairoMakie
using Random
Random.seed!(123)
n = 20
angles = range(0, 2pi, length = n+1)[1:end-1]
x = [cos.(angles); 2 .* cos.(angles .+ pi/n)]
y = [sin.(angles); 2 .* sin.(angles .+ pi/n)]
z = (x .- 0.5).^2 + (y .- 0.5).^2 .+ 0.5.*randn.()
triangulation_inner = reduce(hcat, map(i -> [0, 1, n] .+ i, 1:n))
triangulation_outer = reduce(hcat, map(i -> [n-1, n, 0] .+ i, 1:n))
triangulation = hcat(triangulation_inner, triangulation_outer)
f, ax, _ = tricontourf(x, y, z, triangulation = triangulation,
axis = (; aspect = 1, title = "Manual triangulation"))
scatter!(x, y, color = z, strokewidth = 1, strokecolor = :black)
tricontourf(f[1, 2], x, y, z, triangulation = Makie.DelaunayTriangulation(),
axis = (; aspect = 1, title = "Delaunay triangulation"))
scatter!(x, y, color = z, strokewidth = 1, strokecolor = :black)
f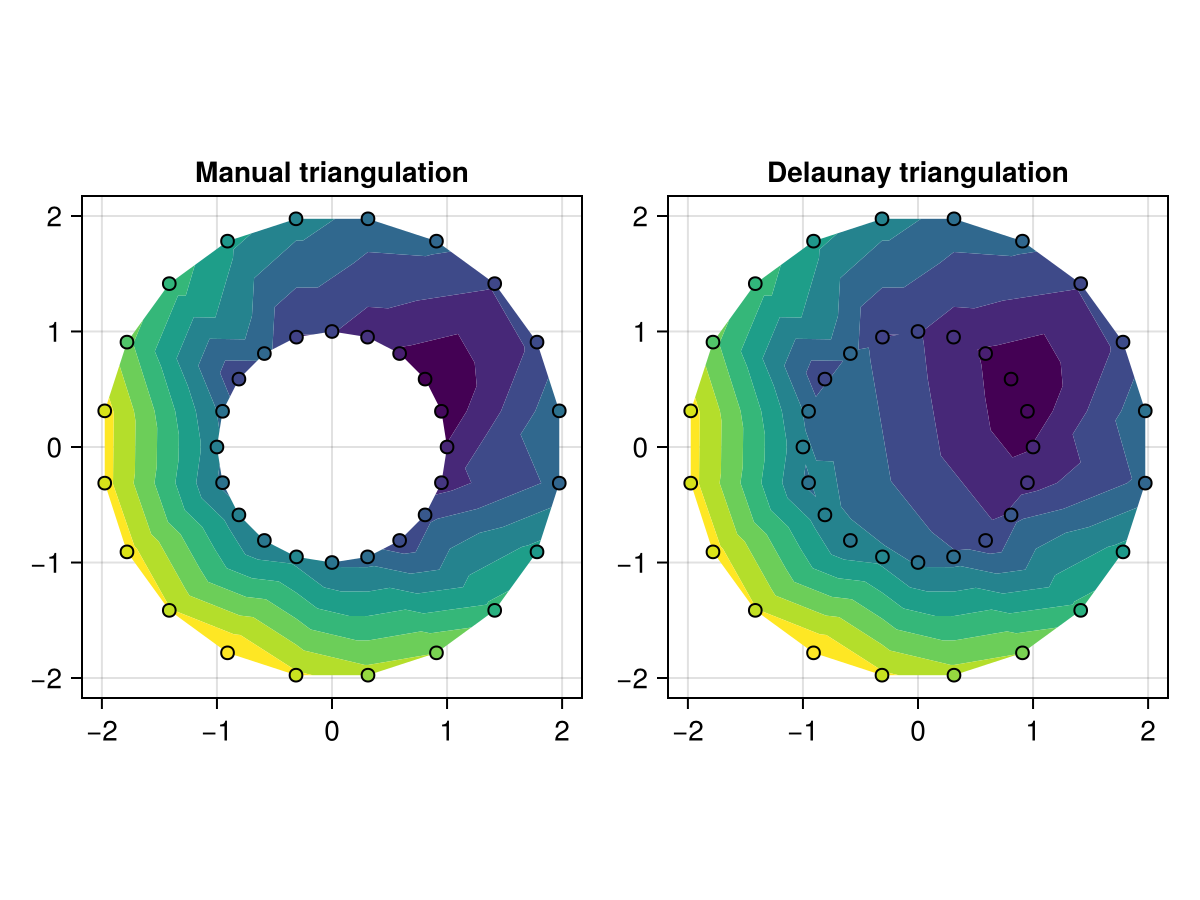
默认情况下, [医]三角帆 执行无约束三角测量。 可以通过使用以下方法实现对三角测量的更大控制,例如允许强制边界https://github.com/DanielVandH/DelaunayTriangulation.jl[DelaunayTriangulation.jl]并将由此产生的三角测量作为 [医]三角帆. 例如,上述环空也可以如下绘制:
</无翻译>
using CairoMakie
using DelaunayTriangulation
using Random
Random.seed!(123)
n=20
角度=范围(0,2pi,长度=n+1)[1:end-1]
x=[cos.(角度);2。*cos。(角度。+pi/n)]
y=[罪。(角度);2。*罪。(角度。+pi/n)]
z=(x.- 0.5).^2+(y.- 0.5).^2 .+ 0.5.*兰德。()
内=[n:-1:1;n]#顺时针内
outer=[(n+1):(2n);n+1]#逆时针outer
boundary_nodes=[[外部],[内部]]
点=[x';y']
tri=triangulate(points;boundary_nodes=boundary_nodes)
f,ax,_=tricontourf(tri,z;
轴=(;方面=1,标题="约束三角测量\nvia DelaunayTriangulation。jl"))
散开!(x,y,color=z,strokewidth=1,strokecolor=:黑色)
f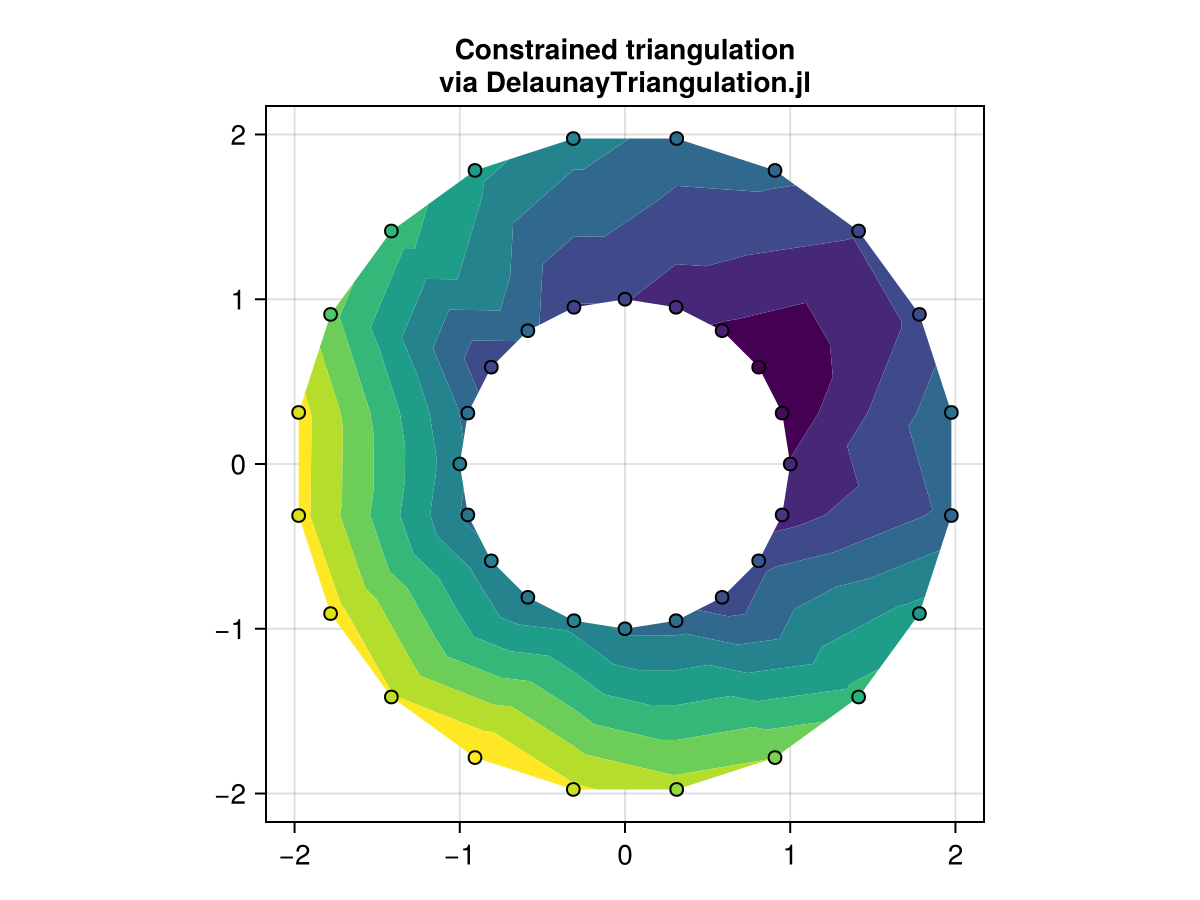
using CairoMakie
using DelaunayTriangulation
## Start by defining the boundaries, and then convert to the appropriate interface
curve_1 = [
[(0.0, 0.0), (5.0, 0.0), (10.0, 0.0), (15.0, 0.0), (20.0, 0.0), (25.0, 0.0)],
[(25.0, 0.0), (25.0, 5.0), (25.0, 10.0), (25.0, 15.0), (25.0, 20.0), (25.0, 25.0)],
[(25.0, 25.0), (20.0, 25.0), (15.0, 25.0), (10.0, 25.0), (5.0, 25.0), (0.0, 25.0)],
[(0.0, 25.0), (0.0, 20.0), (0.0, 15.0), (0.0, 10.0), (0.0, 5.0), (0.0, 0.0)]
] # outer-most boundary: counter-clockwise
curve_2 = [
[(4.0, 6.0), (4.0, 14.0), (4.0, 20.0), (18.0, 20.0), (20.0, 20.0)],
[(20.0, 20.0), (20.0, 16.0), (20.0, 12.0), (20.0, 8.0), (20.0, 4.0)],
[(20.0, 4.0), (16.0, 4.0), (12.0, 4.0), (8.0, 4.0), (4.0, 4.0), (4.0, 6.0)]
] # inner boundary: clockwise
curve_3 = [
[(12.906, 10.912), (16.0, 12.0), (16.16, 14.46), (16.29, 17.06),
(13.13, 16.86), (8.92, 16.4), (8.8, 10.9), (12.906, 10.912)]
] # this is inside curve_2, so it's counter-clockwise
curves = [curve_1, curve_2, curve_3]
points = [
(3.0, 23.0), (9.0, 24.0), (9.2, 22.0), (14.8, 22.8), (16.0, 22.0),
(23.0, 23.0), (22.6, 19.0), (23.8, 17.8), (22.0, 14.0), (22.0, 11.0),
(24.0, 6.0), (23.0, 2.0), (19.0, 1.0), (16.0, 3.0), (10.0, 1.0), (11.0, 3.0),
(6.0, 2.0), (6.2, 3.0), (2.0, 3.0), (2.6, 6.2), (2.0, 8.0), (2.0, 11.0),
(5.0, 12.0), (2.0, 17.0), (3.0, 19.0), (6.0, 18.0), (6.5, 14.5),
(13.0, 19.0), (13.0, 12.0), (16.0, 8.0), (9.8, 8.0), (7.5, 6.0),
(12.0, 13.0), (19.0, 15.0)
]
boundary_nodes, points = convert_boundary_points_to_indices(curves; existing_points=points)
edges = Set(((1, 19), (19, 12), (46, 4), (45, 12)))
## Extract the x, y
tri = triangulate(points; boundary_nodes = boundary_nodes, segments = edges)
z = [(x - 1) * (y + 1) for (x, y) in DelaunayTriangulation.each_point(tri)] # note that each_point preserves the index order
f, ax, _ = tricontourf(tri, z, levels = 30; axis = (; aspect = 1))
f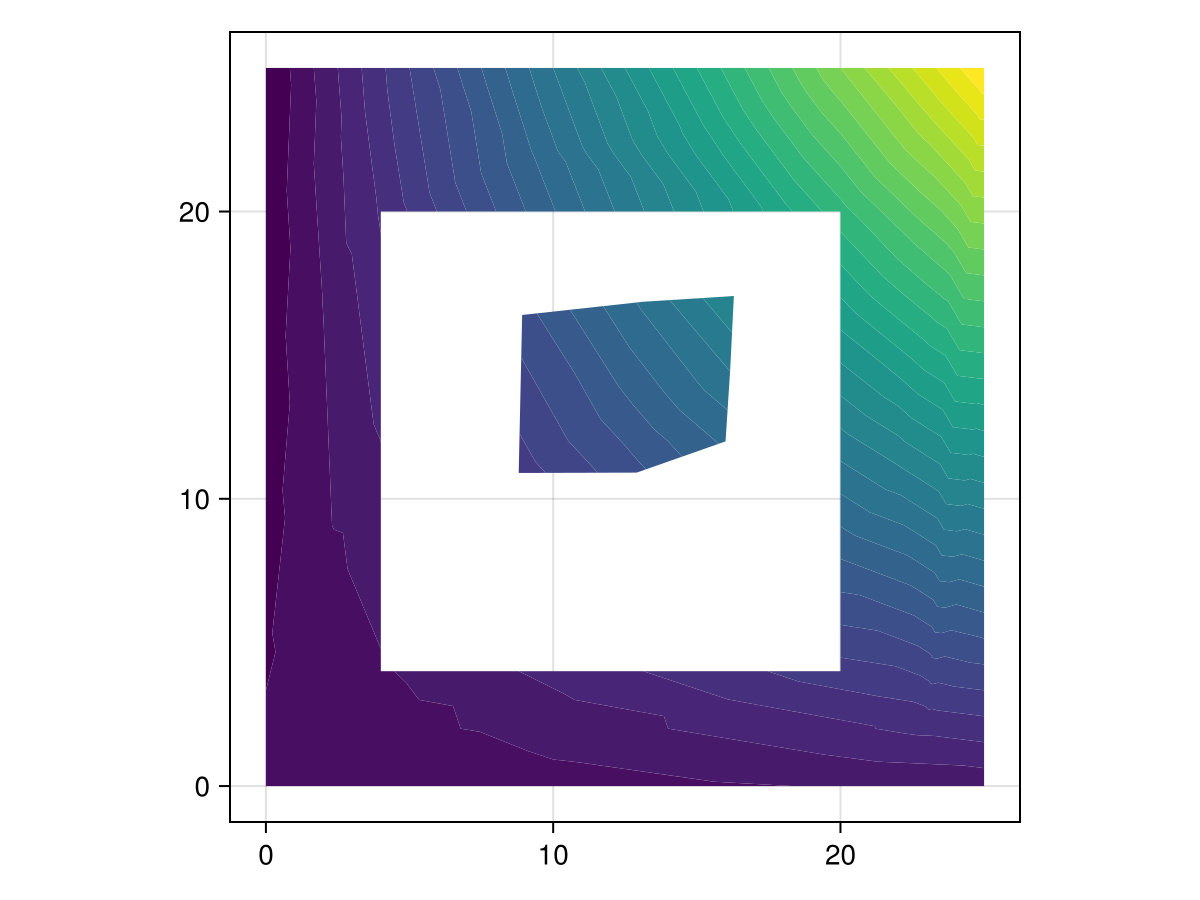
using CairoMakie
using DelaunayTriangulation
using Random
Random.seed!(1234)
θ = [LinRange(0, 2π * (1 - 1/19), 20); 0]
xy = Vector{Vector{Vector{NTuple{2,Float64}}}}()
cx = [0.0, 3.0]
for i in 1:2
push!(xy, [[(cx[i] + cos(θ), sin(θ)) for θ in θ]])
push!(xy, [[(cx[i] + 0.5cos(θ), 0.5sin(θ)) for θ in reverse(θ)]])
end
boundary_nodes, points = convert_boundary_points_to_indices(xy)
tri = triangulate(points; boundary_nodes=boundary_nodes)
z = [(x - 3/2)^2 + y^2 for (x, y) in DelaunayTriangulation.each_point(tri)] # note that each_point preserves the index order
f, ax, tr = tricontourf(tri, z, colormap = :matter)
f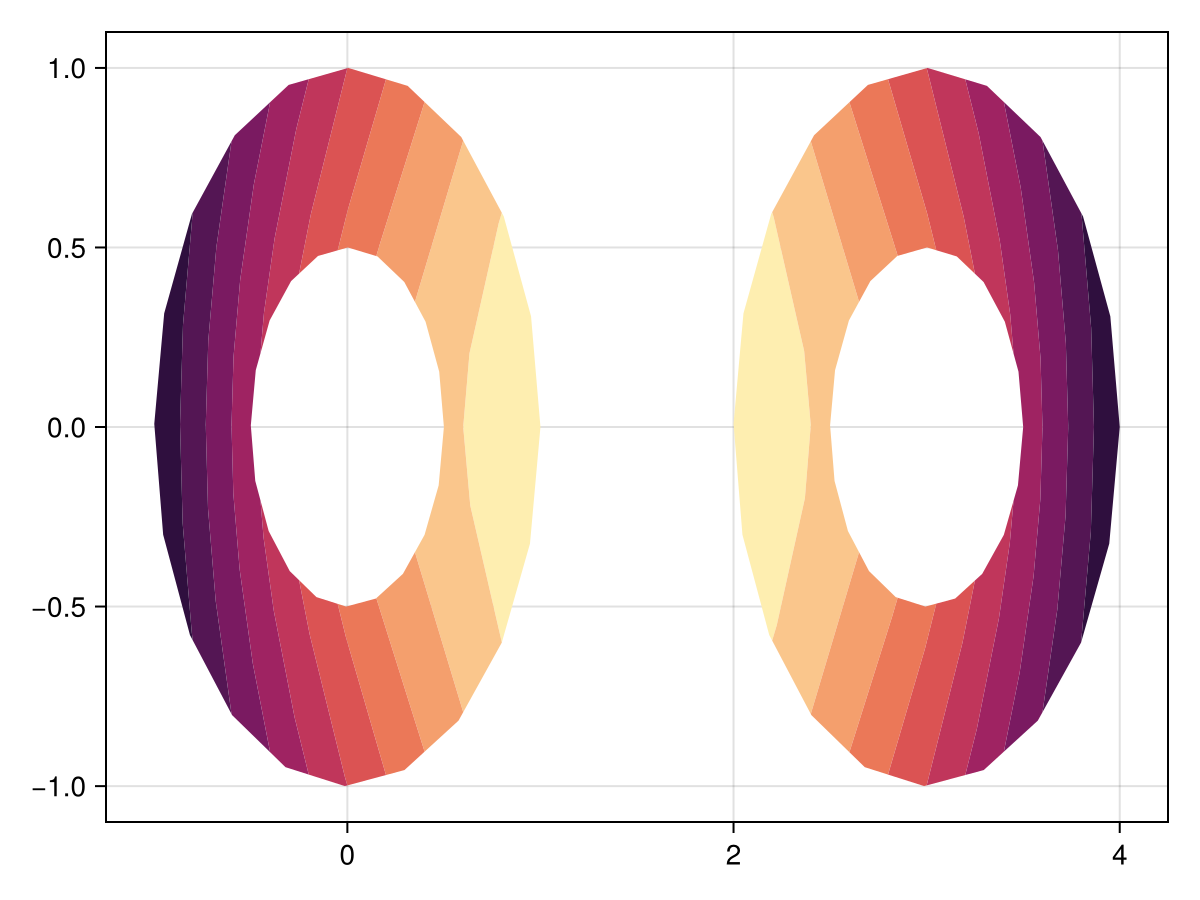
相对模式
using CairoMakie
using Random
Random.seed!(1234)
x = randn(50)
y = randn(50)
z = -sqrt.(x .^ 2 .+ y .^ 2) .+ 0.1 .* randn.()
f, ax, tr = tricontourf(x, y, z, mode = :relative, levels = 0.2:0.1:1)
scatter!(x, y, color = z, strokewidth = 1, strokecolor = :black)
Colorbar(f[1, 2], tr)
f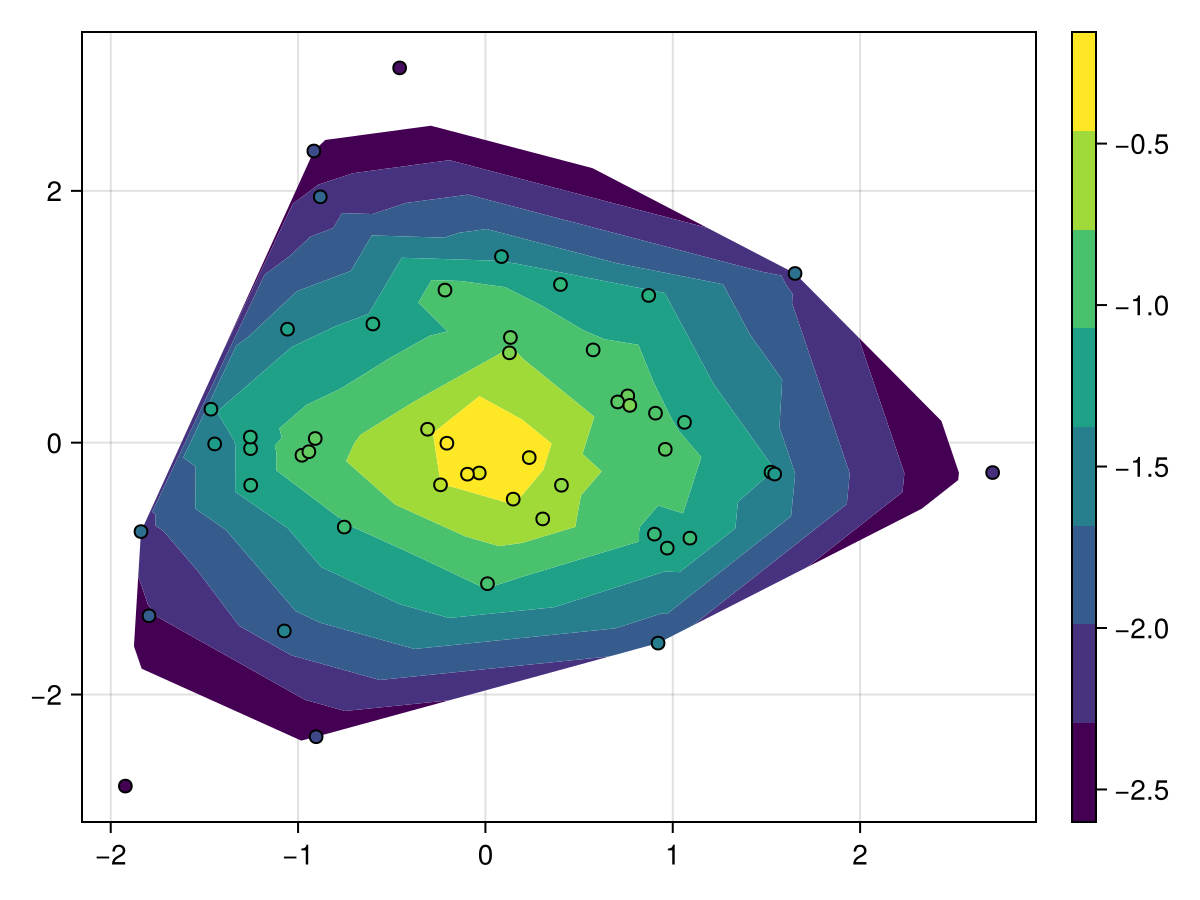
属性
夹式飞机
默认值为 自动的
剪辑平面提供了一种在3D空间中进行剪辑的方法。 您可以设置最多8个向量 平面3f 飞机在这里,后面的情节将被裁剪(即变得不可见)。 默认情况下,剪辑平面继承自父绘图或场景。 您可以删除父 夹式飞机 通过传递 平面3f[].
延伸,延伸
默认值为 什么都没有
这将设置一个可选的附加波段的颜色从最高值 水平 到 最大值(zs). 如果是 :自动,颜色表的高端被挑选,其余的颜色相应地移动。 如果是任何颜色表示,则使用此颜色。 如果是 什么都没有,没有添加带。
延伸,延伸
默认值为 什么都没有
这将设置一个可选的附加波段的颜色从 最小(zs) 至最低值 水平. 如果是 :自动,颜色表的下端被挑选,其余的颜色被相应地移动。 如果是任何颜色表示,则使用此颜色。 如果是 什么都没有,没有添加带。