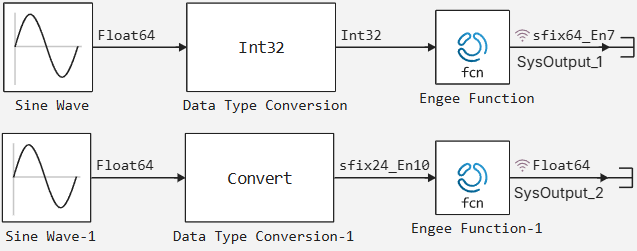
Engee Function
Using Julia code in models.
blockType: EngeeFunction
Path in the library: |
Description
Block Engee Function allows you to use Julia code in Engee models.
| Read more about the Julia programming language on the page Programming. |
| In the block Engee Function It is acceptable to use most of the features of the Julia language. However, the use of the Pkg package manager in the block is not provided. |
Using
To integrate the Julia code into the Engee model, you must:
-
Add a block to the model Engee Function from the Basic section/Custom functions Block libraries
 ;
; -
In settings window
 on the Main tab of the block Engee Function click on the Edit Source Code button to open the source code editor (EngeeFunctionCode):
on the Main tab of the block Engee Function click on the Edit Source Code button to open the source code editor (EngeeFunctionCode):
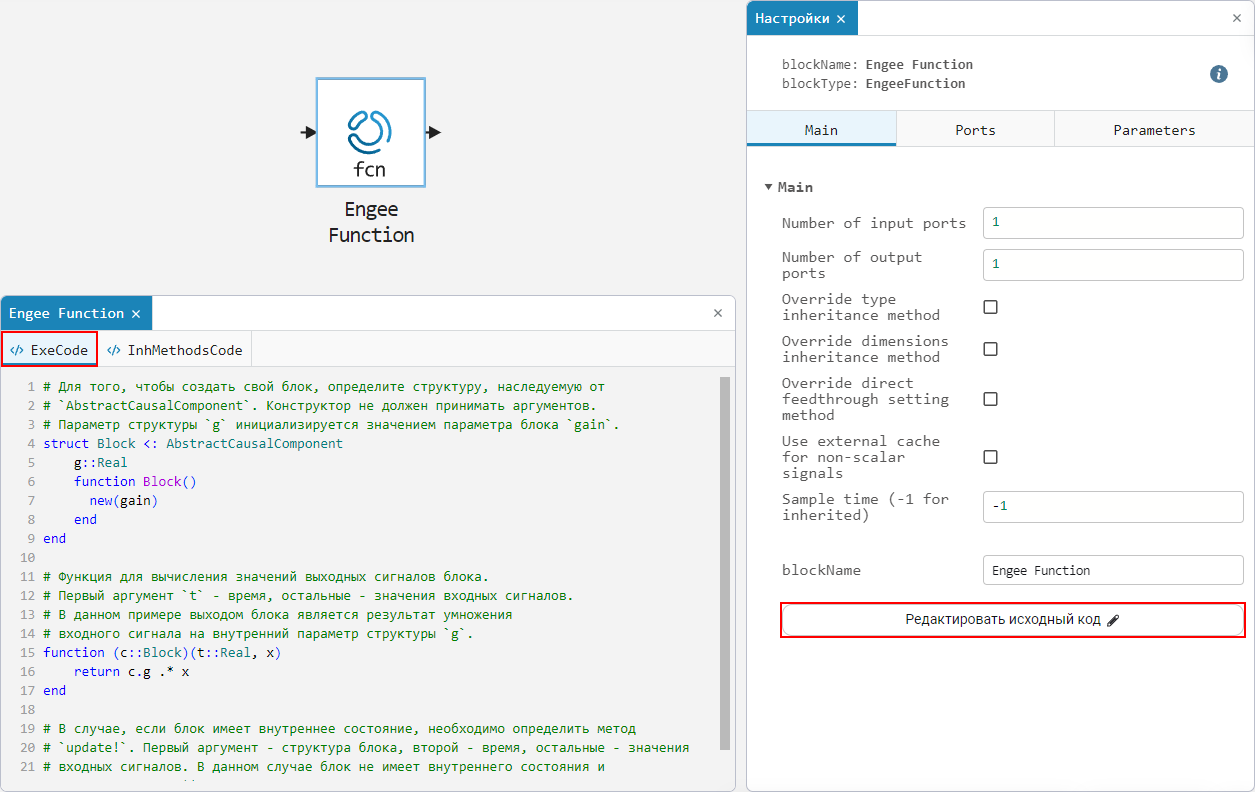
Source code cells
The EngeeFunctionCode source code editor consists of functional cells with Julia code. By default, three cells are available: auxiliary (non-editable), Component struct code and Step method code (cells can be hidden):
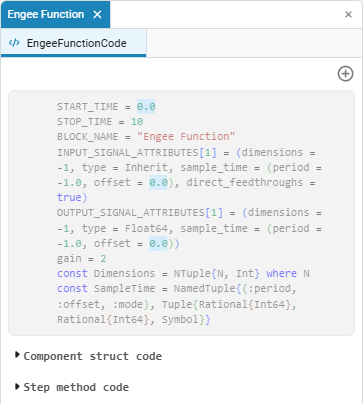
|
To connect additional source code files, you can use the function |
| The entire block code Engee Function you can write in the cell Common code by gaining full control over the component structure, signatures, and number of functions. |
To add/remove other function cells, click on the "Manage methods" button  and check/uncheck the appropriate cells.:
and check/uncheck the appropriate cells.:
 →
→ 
Each cell is responsible for the unique functionality of the block Engee Function. Let’s look at them in more detail:
-
Information cell (non—editable) - automatically displays block variables Engee Function, attributes of input and output signals (dimension, type, discreteness) and other user-defined parameters. Its content is updated dynamically depending on the block settings. The cell is always active, but it is not selected in the method management menu.
 . It has a semi-transparent text that displays hints.
. It has a semi-transparent text that displays hints.
Changing the block parameters affects not only the contents of the information cell, but also the hints in other cells, which are also displayed in translucent text. -
Define component structure — adds a cell Component struct code, which defines the structure of the block component Engee Function (inherited from the type
AbstractCausalComponent). The fields of the structure are defined between non-editable linesstruct Block <: AbstractCausalComponentandend. By default, the parameter is createdg, initialized by the block valuegain, and the constructorBlock()it does not accept arguments.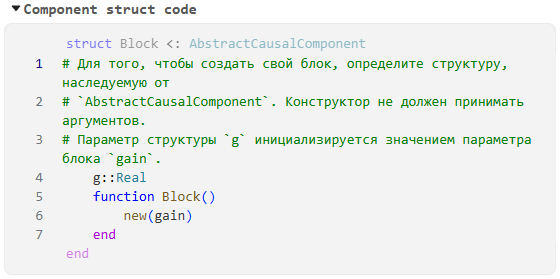
-
Use common code — adds a cell Common code, in which the code is written in free form. By default, the cell is empty. For example, if the standard structure declaration in Component struct code not suitable (due to non-editability
struct Block <: AbstractCausalComponent), then you can disable Define component structure to delete the cell, and define the component structure manually in Common code. The same applies to any functions from the method management menu. — instead of standard cells, you can write your own code in Common code.
— instead of standard cells, you can write your own code in Common code.
Declaring a component and a functor is required to work. Engee Function. If Define component structure and Define step method are disabled, then their code must be set in Common code otherwise, the block will not work. To redefine inheritance functions (Override, see below), you first need to include the corresponding cell, erase its contents, and then write new code in Common code. -
Define step method — adds a cell Step method code, which defines the Step method that calculates the output signals of the block Engee Function. The method signature is generated automatically depending on the values of the corresponding port labels in the Ports tab. The method is represented as a functor (for more information, see here) and is called at each step of the simulation. Fields are defined between non-editable lines
function (c::Block)(t::Real, in1)andend. The first argumentt::Real— simulation time, then input signal variables are transmitted. Calculated output values are returned via a keywordreturn.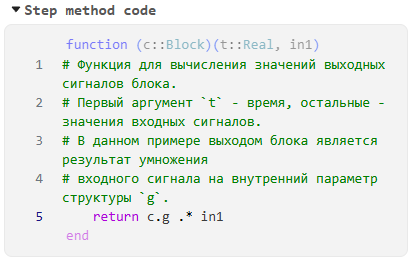
-
Define update method — adds a cell Update method code in which the method
update!updates the internal state of the block Engee Function at each step of the simulation. The first argumentc::Block— block structure, secondt::Real— simulation time, then the input signals are transmitted. If the block has no internal state, then the method can remain empty and simply returnc.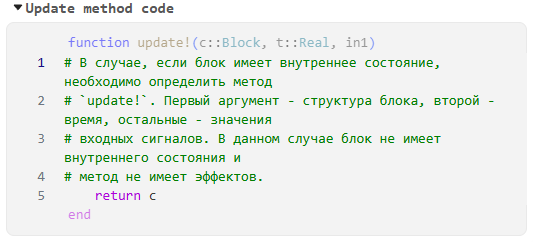
If you need to define multiple methods update!or set a method with a different signature, then you can disable the Update method code cell and write the code in the cell. Common code. The compiler will automatically detect the presence of the methodupdate!and uses it for simulation. -
Define terminate method code — adds the Terminate method code cell, which is executed at the end of the block simulation Engee Function (using the method
terminate!). The first argumentc::Block— block structure. By default, the method does not perform any additional actions and simply returnsc.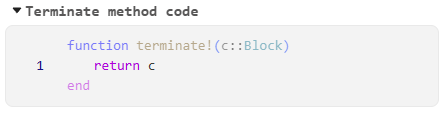
-
Override type inheritance method — adds the Types inheritance method cell, which overrides the type inheritance method.
_ Learn more about the type inheritance method_
Sets the type inheritance method:
-
If the checkbox is unchecked (by default), the types of input/output ports are inherited according to the rules specified in the description of input/output ports.
-
If the box is checked, the input/output port types are inherited according to the rules specified in the function
propagate_typesthe Types inheritance method cells in the source code.-
Function
propagate_typesIt takes in one argument, a vector of types, one type for each input signal, and returns a vector of output types.
-
Default cell code:
function propagate_types(inputs_types::Vector{DataType})::Vector{DataType} # A function that returns an array of output signal types. # It is ignored if the default algorithm is used. # In this case, the type of input signal and the type of # the parameter of the 'gain` block. input_type = first(inputs_types) # promote_type returns the type to which the argument types are given. # during arithmetic operations with objects of these types. output_type = promote_type(input_type, eltype(gain)) return [output_type] endHere, the common element of the input signal and the element of the parameter specified in the block settings in the Setting up the parameters section are taken to inherit types.
-
-
Override dimensions inheritance method — adds a cell Dimensions inheritance method, which redefines the method of inheritance of dimensions.
_ Learn more about the method of dimension inheritance_
Sets the method of inheritance of dimensions:
-
If the checkbox is unchecked (by default), the dimensions of the input/output ports are inherited according to the rules specified in the description of the input/output ports.
-
If the box is checked, the dimensions of the input/output ports are inherited according to the rules specified in the function
propagate_dimensionsthe Dimensions inheritance method cells in the source code.-
Function
propagate_dimensionsIt takes an array of tuples (dimensions) for each input signal and returns an array of dimensions for the output.
-
Default cell code:
function propagate_dimensions(inputs_dimensions::Vector{<:Dimensions})::Vector{<:Dimensions} # A function that returns an array of output signal dimensions. # It is ignored if the default algorithm is used. # In this case, the dimensions of the input signal are taken into account and # the parameter of the 'gain` block. input_dimensions = first(inputs_dimensions) mock_input = zeros(input_dimensions) mock_output = mock_input .* gain return [size(mock_output)] endHere, to inherit dimensions, an array with the necessary dimensions (mock_input) is taken, consisting of zeros, and multiplied by the element of the parameter specified in the block settings in the Setting up the parameters section, after which its dimension is taken.
-
-
Use common method for types and dimensions inheritance — adds the Common types and dimensions inheritance method cell, which uses a common method to redefine inheritance of types and dimensions simultaneously.
_ Learn more about the method of inheritance of types and dimensions_
Unlike specific methods for types (Types inheritance method) or dimensions (Dimensions inheritance method), the general method includes both types and dimensions at the same time:
-
If unchecked (by default), the general method is ignored, the dimensions and types of input/output ports are inherited according to the rules specified in the description of the input/output ports or in the inheritance methods Override type inheritance method (if enabled) and Override dimensions inheritance method (if enabled).
-
If the box is checked, the dimensions and types of input/output ports are inherited according to the rules specified in the function
propagate_types_and_dimensionscells Common types and dimensions inheritance method in the source code.
Default cell code:
function propagate_types_and_dimensions(inputs_types::Vector{DataType}, inputs_dimensions::Vector{<:Dimensions})::Tuple{Vector{DataType}, Vector{<:Dimensions}} # A function that returns an array of signal types and an array # the dimensions of the output signals. This function can be used # if necessary, redefine the inheritance algorithm at the same time. # types of signals, and an algorithm for inheritance of dimensions. outputs_types = propagate_types(inputs_types) outputs_dimensions = propagate_dimensions(inputs_dimensions) return outputs_types, outputs_dimensions endDependencies
To use this cell, select the Override type inheritance method and Override dimensions inheritance method checkboxes.
-
-
Override sample time inheritance method — adds a cell Sample times inheritance method, which redefines the inheritance method of the calculation step.
_ Learn more about the method of inheritance of the calculation step_
The structure code of the calculation step SampleTimeand functionspropagate_sample_timesThey will not be automatically added to the EngeeFunctionCode source code of older Engee models. To refine the old models, add the structure of the calculation step and the function yourself.Sets the inheritance method for the calculation step:
-
If the checkbox is unchecked (by default), the preset method of inheritance of the calculation step is used (by default
Default) from the Sample time inheritance method parameter of the Advanced tab. Read more about the pre-installed methods. below. -
If the checkbox is checked, the preset methods of the Advanced tab are ignored (the parameter is unavailable), an independent method is used from the Sample times inheritance method cell in the EngeeFunctionCode source code.
To use an independent method, you need to find the function string.
propagate_sample_timesand manually set the desired calculation step.Default cell code:
function propagate_sample_times(inputs_sample_times::Vector{SampleTime}, fixed_solver::Bool)::SampleTime # A function that returns the sampling time of a block. # It is used only in the `Custom` inheritance mode. # The fixed_solver parameter indicates whether the solver is being used. # with a constant step (true) or with a variable step (false). # A more complex example of working with time inheritance # The block sampling can be viewed in the documentation. return first(inputs_sample_times) endwhere the calculation step has the structure:
const SampleTime = NamedTuple{(:period, :offset, :mode), Tuple{Rational{Int64}, Rational{Int64}, Symbol}} -
-
Override direct feeding setting method — adds a cell Direct feeding setting method that defines a direct end-to-end connection.
_ Learn more about the definition of a direct end-to-end connection_
Defines a direct end-to-end connection:
-
If the checkbox is unchecked (by default), then a direct end-to-end connection is not available. This means that the output signal will not be controlled by the value of the input port and allows the unit to open loops.
-
If this option is selected, a direct end-to-end connection is available. This means that the output signal is controlled directly by the value of the input port.
Default cell code:
function direct_feedthroughs()::Vector{Bool} # A function that returns an array of Boolean values defining, # end-to-end connections. If the ith element of the array is true, # the ith port has an end-to-end connection. # It is ignored if the default algorithm is used. return [true] endexample:
function direct_feedthroughs()::Vector{Bool} if gain == 2 return [false] else return [true] end end -
Constants and functions for obtaining attributes
In order to find out the types, sizes, and other auxiliary information in the block executable code, use the following constants inside your code Engee Function:
-
BLOCK_NAME— the name of the block. Each block added to the Engee canvas has a name that can be accessed through this constant. For example, you can refer to BLOCK_NAME during error initialization to output the block name in it. -
START_TIME— start the simulation from the model settings. -
STOP_TIME— end of the simulation from the model settings. -
INPUT_SIGNAL_ATTRIBUTES— lists of attributes for each input port. For example, to find out the attributes of the first input signal, useINPUT_SIGNAL_ATTRIBUTES[1], where1— the first input port of the unit Engee Function. -
OUTPUT_SIGNAL_ATTRIBUTES— lists of attributes for each output port. For example, to find out the attributes of the first output signal, useOUTPUT_SIGNAL_ATTRIBUTES[1], where1— the first output port of the unit Engee Function.
To find out more information about a specific block port, you can refer to the attributes of its signal by adding a dot . after the constant INPUT_SIGNAL_ATTRIBUTES[i], where [i] — the number of the input port, and OUTPUT_SIGNAL_ATTRIBUTES[i], where [i] — the number of the output port, respectively. You can find out more information through the following contact functions:
-
dimensions— the dimension of the signal. Can be shortened todims. -
type— the type of signal. Can be shortened totp. -
sample_time— the calculation step. It is a structure similar to the attributes of signals, which can be accessed through a dot. .. Two conversion functions are available:-
period— the period of the calculation step. Full conversion function —sample_time.period. Can be shortened tost.p. -
offset— offset of the calculation step. Full conversion function —sample_time.offset. Can be shortened tost.o.
-
-
direct_feedthrough— indicates whether the loop port opens. It is used only for input ports (checks attributes only for the input port). Can be shortened todf.
Model Example Engee Function with all constants and conversion functions:
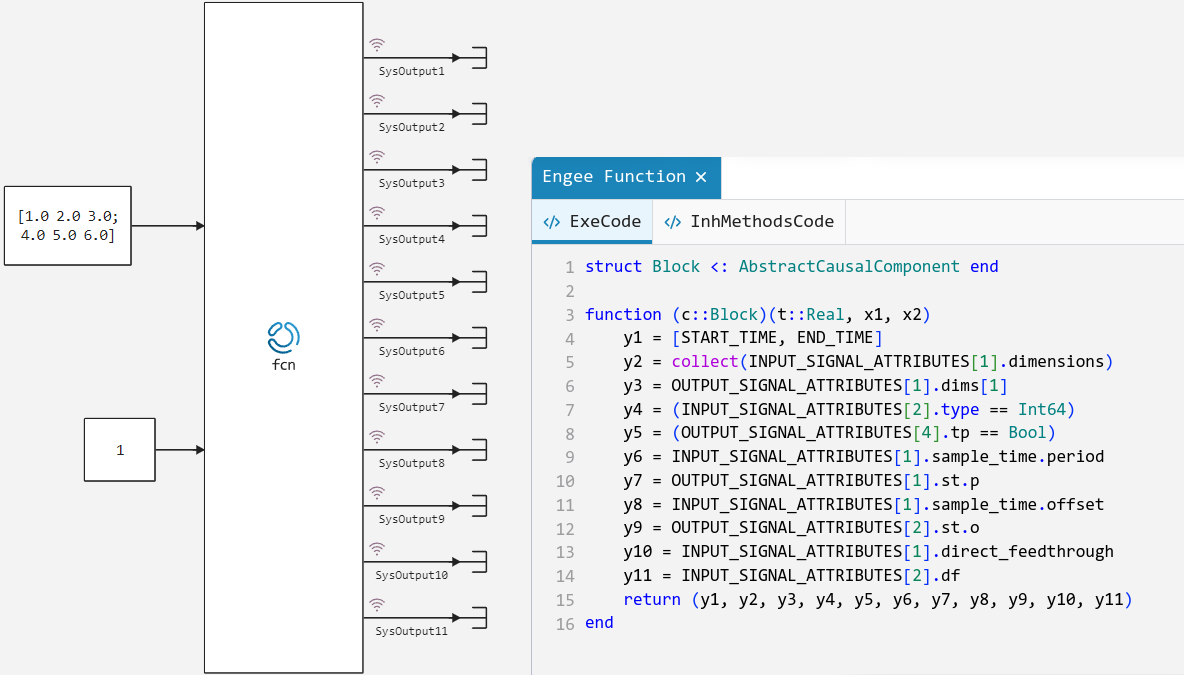
struct Block <: AbstractCausalComponent end
function (c::Block)(t::Real, x1, x2)
y1 = [START_TIME, STOP_TIME]
y2 = collect(INPUT_SIGNAL_ATTRIBUTES[1].dimensions)
y3 = OUTPUT_SIGNAL_ATTRIBUTES[1].dims[1]
y4 = (INPUT_SIGNAL_ATTRIBUTES[2].type == Int64)
y5 = (OUTPUT_SIGNAL_ATTRIBUTES[4].tp == Bool)
y6 = INPUT_SIGNAL_ATTRIBUTES[1].sample_time.period
y7 = OUTPUT_SIGNAL_ATTRIBUTES[1].st.p
y8 = INPUT_SIGNAL_ATTRIBUTES[1].sample_time.offset
y9 = OUTPUT_SIGNAL_ATTRIBUTES[2].st.o
y10 = INPUT_SIGNAL_ATTRIBUTES[1].direct_feedthrough
y11 = INPUT_SIGNAL_ATTRIBUTES[2].df
return (y1, y2, y3, y4, y5, y6, y7, y8, y9, y10, y11)
endWorking with fixed point and custom buses
Block Engee Function, and also command prompt  Engee, support fixed point operation (
Engee, support fixed point operation (Fixed) and custom tire types (BusSignal). These constructs help to control the behavior of operations when working with integer, real, fixed, and complex data types.
Fixed point types and functions (Fixed-Point)
In the article Fixed-Point arithmetic in Engee It describes how to work with a fixed point in Engee. The constructions given in the article are also valid for the block Engee Function, this is how the block supports:
-
FixedPoint— the abstract type of all fixed numbers; -
Fixed— a specific type of fixed number, created manually with the bit representation specified; -
fi(…)— creating a type valueFixedusing a numeric value and representation parameters; -
fixdt(…)— creation of the Fixed type with indication of the sign, width and number of fractional bits.
For example:
a = fi(5, 1, 16, 4) # Signed number, 16 bits, 4 fractional
b = fi(10, 0, 8, 0) # An unsigned integer of 8 bits
T = fixdt(1, 24, 8) # Fixed type with 24 bits, 8 of them are fractional
c = Fixed(0x01ff, T) # Creating a fixed number directly from the bit representationFixed numbers in Engee Function may:
-
Send as parameters;
-
Use in the component structure (cell Component struct code);
-
Perform arithmetic with them using
emul,esum,edivin the Step method code cell (for more information, see Conversion functions and typed arithmetic operations:econvert,esum,emul,ediv); -
Apply to calculations in
propagate_types(…),propagate_dimensions(…).
Working with custom tire types (BusSignal)
Custom bus types allow you to specify the types of input and output signals in the form of structured tuples (NamedTuple) with a description of the names, types, and dimensions inside Engee Function. Available functions:
-
BusSignal{…}— type of bus with names, types and dimensions; -
get_bus_names(type)— get a list of signal names; -
get_bus_types(type)— get the types of signals; -
get_bus_dimensions(type)— get the dimensions of the signals; -
get_names_types_dims(type)— get everything at once; -
get_bus_signal_type(::NamedTuple)— identify the typeBusSignalby value.
An example of determining and analyzing the type of tire:
bus = (a = 1, b = [2.0, 3.0], c = (x = 3, y = 4))
bus_type = get_bus_signal_type(bus)
get_bus_names(bus_type) # => (:a, :b, :c)
get_bus_types(bus_type) # => (Int64, Vector{Float64},
# BusSignal{(:x, :y), Tuple{Int64, Float64}, ((), ())})
get_bus_dimensions(bus_type) # => ((), (2,), ((), ()))You can explicitly describe the tires:
MyBus = BusSignal{(:s1, :s2), Tuple{Int64, Float64}, ((), ())}
signal = MyBus((s1 = 5, s2 = 6.4))Nested buses are also supported.:
Inner = BusSignal{(:x, :y), Tuple{Int, Int}, ((), ())}
Outer = BusSignal{(:a, :b), Tuple{Float64, Inner}, ((), ())}Usage in the block Engee Function
Types Fixed and BusSignal It can be used in different parts of the block. Engee Function:
-
In the block parameters, you can set fixed point values using
fi(…), and also transfer the bus structures asNamedTuple. The type of bus can be determined automatically viaget_bus_signal_type(…). -
In the Common code cell, you can define data types (
Fixed,BusSignal{…}), component structures (struct Block), create auxiliary functions or initialize values. You can also move the main logic here if Step method code or Component struct code are disabled. -
In the cell Component structure code — when describing the fields of the structure, you can use values like
Fixed, as well as the typesBusSignalif the fields are composite signals. -
The Step method code cell implements the main logic of the block. Here, fixed numbers and bus signals can participate in calculations, comparisons, and structure processing.
-
In the cell Types inheritance method — you can use the types
FixedandBusSignalto analyze the inputs and specify the output type of the component. -
In the Dimensions inheritance method cell, you can use the data
Fixedand the values from the buses to determine the dimensions of the output signals. -
In the Update method code cell, if the block has an internal state, fields like
FixedorBusSignalIt can be used to store or change this state at each step of the simulation. -
In the Terminate method code cell, these types can be used to record the final state if the structure contains the appropriate fields.
-
In the Common types and dimensions inheritance method cell, if both types and dimensions need to be processed simultaneously.,
FixedandBusSignalThey can also participate in the calculation logic.
Therefore, Fixed, fi(…), fixdt(…), BusSignal and get_bus The functions are applicable in all aspects of the configuration and operation of the unit. Engee Function — both at the execution stage and at the generation stage of the type and dimension of the signal. They can be freely used both in the parameters and in the source code in all cells (if they work correctly).
Conversion functions and typed arithmetic operations: econvert, esum, emul, ediv
In the block Engee Function, as well as in command line  Engee features are available that allow you to perform arithmetic operations with an output type, convert values between types with rounding and overflow control, and pre-determine the result type using specialized rules (
Engee features are available that allow you to perform arithmetic operations with an output type, convert values between types with rounding and overflow control, and pre-determine the result type using specialized rules (_promote_type). These functions are used in logic Engee Function, written in the source code cells Step method code, Common code and others.
Available functions:
-
econvert— conversion of values between types; -
esum,esub,emul,ediv— arithmetic operations with the output type assignment; -
emul!— matrix multiplication with result caching; -
*_promote_type— output functions based on input types.
| These functions can be applied to both scalars and arrays. The result is always returned in a type explicitly specified by the user (or output automatically), which makes the block behavior stable and expected. |
Supported types
All the functions in this set work with the following types:
-
The real ones:
Float16,Float32,Float64 -
Integers:
Int8,Int16,Int32,Int64,Int128,UInt8,UInt16,UInt32,UInt64,UInt128 -
Logical:
Bool -
Fixed:
Fixed(created viafi(…)orfixdt(…)) -
Comprehensive:
Complex{T}, whereT— any of the above types
Functions can also be used with arrays and vectorized expressions using dot syntax (.). Next, let’s look at the functions in more detail.
Converting numbers using econvert
Function econvert allows you to convert a value to a specified type by specifying the rounding method and the overflow handling method.:
econvert(type::Type{T1}, var::T2; rounding_mode::RoundingMode=RoundDown, overflow::Bool=true)Here:
-
type— the type to convert the value to. Ifvar— a complex number, the basic real type is indicated. For example,econvert(Float32, Complex{Int16}(1 + 2im))it will returnComplex{Float32}; -
var— value for conversion; -
rounding_mode— the rounding method (RoundDown,RoundUp,RoundNearest,RoundNearestTiesAway,RoundToZero); -
overflow— iftrue, then the overflow behavior (wrap) is used; iffalsesaturation is enabled — the value is limited by the type range.
Function econvert It can be used for type conversion before comparisons, inside arithmetic expressions, when processing signals in conditions and other scenarios.
Arithmetic with type control using esum, esub, emul, ediv, emul!
Functions of typed arithmetic operations esum, esub, emul, ediv, emul! they have the same interface:
esum(x1, x2, out_type, overflow=true, rm=RoundDown)
esub(x1, x2, out_type, overflow=true, rm=RoundDown)
emul(x1, x2, out_type, overflow=true, rm=RoundDown)
ediv(x1, x2, out_type, overflow=true, rm=RoundDown)
emul!(cache, x1, x2, out_type, overflow=true, rm=RoundDown)Arguments:
-
x1,x2— operation arguments (scalars or arrays are allowed); -
out_type— the type in which the result is produced and returned; -
overflow— enabling overflow (true) or saturation (false); -
rm— the rounding method (see the list above).
Functions esum, esub, emul, ediv returns the value corresponding to the specified out_type.
Function emul! It is used to speed up when working with matrices: it does not create a new array, but writes the result to an already allocated one. cache. It is important that eltype(cache) coincided with out_type.
The result depends on the type out_type: it affects not only the final result, but also the behavior of intermediate calculations — which is especially important for Fixed and Complex.
Inferring the type of result using *_promote_type
If the block parameters (for example, SumType or MulType) are set as a string "Inherit", the type of result is determined automatically based on the types of input data using the functions *_promote_type.
If you need to calculate the result type of an operation, then use the listed functions:
-
Defines the output type when adding
nvalues of the same typeT:sum_promote_type(::Type{T}, n::Integer=1, hdlsetup::Bool=false) -
Defines the output type when two different types are added together
T1andT2bynvalues:sum_promote_type(::Type{T1}, ::Type{T2}, n::Integer=1, hdlsetup::Bool=false) -
Defines the output type when adding an arbitrary number of arguments with different types.:
sum_promote_type_from_inputs(types::Type...; hdlsetup::Bool=false) -
Determines the type of accumulator when adding up
nvalues of the same typeT:sum_accumulator_promote_type(::Type{T}, n::Integer=1, hdlsetup::Bool=false) -
Determines the type of battery when two different types are added together
T1andT2bynvalues:sum_accumulator_promote_type(::Type{T1}, ::Type{T2}, n::Integer=1, hdlsetup::Bool=false) -
Defines the type of accumulator when adding an arbitrary number of arguments with different types.:
sum_accumulator_promote_type_from_inputs(types::Type...; hdlsetup::Bool=false) -
Defines the output type when multiplying values of the same type
T:mul_promote_type(::Type{T}, hdlsetup::Bool=false) -
Defines the output type when two different types are multiplied.
T1andT2:mul_promote_type(::Type{T1}, ::Type{T2}, hdlsetup::Bool=false) -
Defines the output type when dividing a single type value
T:div_promote_type(::Type{T}, hdlsetup::Bool=false) -
Defines the output type when dividing the type value
T1on the type valueT2:div_promote_type(::Type{T1}, ::Type{T2}, hdlsetup::Bool=false)Here:
-
hdlsetup— a logical parameter that determines whether to take into account the specifics of the hardware platform (TargetHardware). By default:hdlsetup = TargetHardware == "C" ? false : true
-
The functions are conveniently used in the Types inheritance method cell to accurately determine the output block type based on inputs and parameters.
Usage example
Below is an example of a component that implements the expression a*x + b. The types of intermediate multiplication and final addition are set using the parameters MulType and SumType. If specified "Inherit", then the type is output automatically.
example of using a*x + b
Parameters Engee Function:
a = fi(5, 1, 16, 4)
b = fi(11, 1, 24, 7)
MulType = "Inherit"
SumType = "Inherit"The block code (in the cell Common code, Dimensions inheritance method and Types inheritance method):
-
Cell Common code:
struct Block{SumType, MulType, aType, bType} <: AbstractCausalComponent a::aType b::bType function Block() sum_type = OUTPUT_SIGNAL_ATTRIBUTES[1].type mul_type = if MulType == "Inherit" mul_promote_type(INPUT_SIGNAL_ATTRIBUTES[1].type, eltype(a)) else MulType end new{sum_type, mul_type, typeof(a), typeof(b)}(a, b) end end -
Cell Dimensions inheritance method:
function propagate_dimensions(inputs_dimensions::Vector{<:Dimensions})::Vector{<:Dimensions} input_dimensions = first(inputs_dimensions) mock_input = zeros(input_dimensions) mock_output = mock_input .* a .* b return [size(mock_output)] end -
Cell Types inheritance method:
function propagate_types(inputs_types::Vector{DataType})::Vector{DataType} mul_type = if MulType == "Inherit" mul_promote_type(inputs_types[1], eltype(a)) else MulType end sum_type = if SumType == "Inherit" sum_promote_type(mul_type, eltype(b)) else SumType end return [sum_type] end
Thus, the functions econvert, esum, emul, ediv And the rules promote_type they allow you to control the types and behavior of calculations within a block. Engee Function. They support all major numeric types, including fixed point and complex values, and can be used in calculations, comparisons, inheritance logic, and component behavior tuning using a block. Engee Function.
Diagnostic functions warning, stop_simulation, pause_simulation, info
In the source code of the block Engee Function functions are also available warning, stop_simulation, pause_simulation and info, which allow you to interact with the diagnostic system of the model at the simulation stage, allowing you to output messages in diagnostic window  . These functions can be used inside the following source code cells:
. These functions can be used inside the following source code cells:
-
Component struct code
-
Step method code
-
Update method code
-
Terminate method code
-
Common code
|
Functions So, although these functions are formally allowed in the Component struct code cell, in practice their placement there does not make sense: this cell is intended solely to describe the block structure, and not for executable logic. In order for diagnostic functions to work correctly, they must be placed inside the supported simulation methods: Step method, Update method, Terminate method, or in Common code if the corresponding method is redefined there. Example of correct placement:
|
By analogy, you can override any supported method called during the simulation (for example, update!, terminate, step), in the Common code cell manually — if you disable the corresponding standard cell (for example, Define update method, Define step method, etc.).
For correct operation in the cell Common code functions warning, stop_simulation, pause_simulation and info can be used:
-
Inside functions that redefine the behavior of methods responsible for executing the model, such as
step,update!,terminate!. For example, if the functor normally specified in the Step method code cell is defined in Common code, then the diagnostic functions inside it will work correctly. -
Inside auxiliary functions that are called from the methods responsible for executing the model. That is, if the auxiliary function is defined in Common code and is used, for example, in
step, then calls to diagnostic functions inside it will also be executed correctly.Redefinition update!or other methods do not replace the required implementation.step(function (c::Block)(t, in…)). Engee requires this function as an entry point to the simulation.
An example of a correct redefinition update! in Common code:
# Structure with Component structure code (if disabled, it must be rendered in Common code)
struct Block <: AbstractCausalComponent
g::Real
function Block()
new(gain)
end
end
# Step method (a mandatory method called at each step of the simulation)
function (c::Block)(t::Real, in1)
c = update!(c, t, in1)
return c.g .* in1
end
# The redefined update method!
function update!(c::Block, t::Real, in1)
if t == 5.0
info("update triggered at t = $t") # diagnostic message
end
return c
endAs a result, the following messages will be received in the diagnostic window of the model:

Next, let’s take a closer look at the diagnostic functions themselves.:
-
warning— functionwarning(msg::String)displays a warning message. The simulation continues. This can be useful for pointing out non-critical issues or conditions that require attention but do not stop execution. Example:if t == 5.0 || t == 7.5 warning("time == $t") end -
stop_simulation— functionstop_simulation(msg::String)immediately ends the simulation and displays a completion message. It is used to indicate a critical condition under which continued modeling is impossible or undesirable. Example:if t == 5.0 stop_simulation("time == $t") end -
pause_simulation— functionpause_simulation(msg::String)pauses the simulation and displays the specified pause message. The simulation can be resumed manually using the button Continue:
This function can be useful for analyzing the state of the model at a given time. Example:
if t == 5.0 pause_simulation("time == $t") end -
info— functioninfo(msg::String)displays an information message. It is used to display intermediate values without affecting the execution of the simulation. Example:if t == 5.0 || t == 7.5 info("time == $t") end
Ports
Entrance
Input Port — input port
+
scalar | vector | the matrix
Details
An input port specified as a scalar, vector, or matrix.
Configure the input port in the Ports tab of the block using the following options:
-
Label — specify the name of the input port. By default, the Label cell is empty (the name is not specified).
-
Type — input signal data type. Choose one of the options:
-
A certain type (all except
Inherit) — it is checked that a certain type of signal is being sent to the input port. Select a specific data type for the input port. Supported signals:Float16,Float32,Float64,ComplexF32,ComplexF64,Bool,Int8,Int16,Int32,Int64,Int128,UInt8,UInt16,UInt32,UInt64,UInt128. -
Inherit(by default) — inherits the data type from the associated block. It can be any type of data.
-
-
Size — the dimension of the input signal:
-
Inheritance of all dimensions (
-1by default) — inherits the dimension of the signal applied to the input port (the signal can have any dimension). -
Defined dimensions — The input signal must have a specified number of elements. The dimensions are specified in Julia notation (as a tuple), for example,
(2,)for a one-dimensional signal consisting of two elements, or(2, 3, 4)for the multidimensional. If specified-1, then the dimension is inherited. -
Inheriting one of the dimensions — inherits the dimension of the signal sent to the input port with an explicit indication of the data structure. For example,
(-1, 2)— it is expected that the first dimension is inherited, and the second is set explicitly.
-
-
Output bus type — input bus type, replaces the dimension of the input signal Size if the data type of the input signal Type is selected
BusSignal(the tire). The default value isBusSignal{(), Tuple{}, ()}. To block Engee Function I understood which bus will come to the input, it is enough to set Type to the valueInherit. Explicit type indication is only necessary for the output signal.Block Engee Function It does not inherit buses to the output ports, although it can receive them to the inputs. To inherit buses on the output ports (for transmission to other blocks), you must explicitly specify the bus type in the Output bus type parameter. -
Direct feedthrough — defines a direct end-to-end connection:
-
If the checkbox is selected (by default), then a direct end-to-end connection is available. This means that the output signal is controlled directly by the value of the input port.
-
If the checkbox is unchecked, then a direct end-to-end connection is not available. This means that the output signal will not be controlled by the value of the input port and allows the unit to open loops.
-
Output
Output port — output port
+
scalar | vector | the matrix
Details
An output port specified as a scalar, vector, or matrix.
Configure the output port in the Ports tab of the block using the following options:
-
Label — specify the name of the output port. By default, the Label cell is empty (the name is not specified).
-
Type — the data type of the output signal. Choose one of the options:
-
A certain type (all except
Inherit) — we determine the data type of the output signal. Select a specific data type for the output signal. Supported signals:Float16,Float32,Float64,ComplexF32,ComplexF64,Bool,Int8,Int16,Int32,Int64,Int128,UInt8,UInt16,UInt32,UInt64,UInt128. -
Inherit(by default) — inherits the data type of the output signal. Calculates the smallest common type when there are several input signals of different types. It can be any type of data.
-
-
Size — the dimension of the output signal:
-
Inheritance of all dimensions (
-1by default) — inherits the dimension of the signal applied to the output port. The output signal will have the dimensions obtained as a result of the broadcast mechanism — Julia will automatically expand the dimension of a smaller data array to a larger dimension in order to correctly inherit the dimension. -
Defined dimensions — the output signal must have a specified number of elements. The dimensions are specified in Julia notation (as a tuple), for example,
(2,)for a one-dimensional signal consisting of two elements, or(2, 3, 4)for the multidimensional. If specified-1, then the dimension is inherited. -
Inheriting one of the dimensions — inherits the dimension of the signal sent to the output port with an explicit indication of the data structure. For example,
(-1, 2)— it is expected that the first dimension is inherited, and the second is set explicitly.
-
-
Output bus type — the output bus type, replaces the dimension of the input signal Size if the data type of the output signal Type is selected
BusSignal(the tire). The default value isBusSignal{(), Tuple{}, ()}. To block Engee Function If you have issued a tire to the outlet, you must explicitly specify its type.
Parameters
Main
Number of input ports — defines the number of input ports
+
1 (default)
Details
Defines the number of input ports of the block. The value of the Number of input ports parameter will correspond to the number of input ports.
Number of output ports — defines the number of output ports
+
1 (default)
Details
Defines the number of output ports of the block. The value of the Number of output ports parameter will correspond to the number of output ports.
Sample time — the interval between calculation steps
+
-1 (default)
Details
Specify the interval between the calculation steps as a non-negative number. To inherit the calculation step, set this parameter to −1.
Advanced
Use external cache for non-scalar output — use external cache for non-scalar outputs
+
disabled (by default) | enabled
Details
Specify the use of an external cache for a non-scalar (multidimensional) output signal to save Engee RAM. Used if the block has Engee Function only one output port:
-
If the checkbox is unchecked (by default), the external cache is not used.
-
If the box is checked, the output signal can accept an additional argument.
cache, which must be taken into account in the EngeeFunctionCode source code. If the unit has one output port, then in the cell Step method code argumentcacheit is automatically added to the list of function arguments, except when the port dimension is explicitly specified as()(scalar). In the source code, it is required to write functors depending on the dimension of the output signal. The functors can be defined in a cell Common code:-
If the output signal is scalar:
function (c::Block)(t::Real, x) return c.g * x end -
If the output signal is non-scalar:
function (c::Block)(t::Real, cache, x) cache .= c.g .* x nothing endwhere
t— time,x— the argument (information from the input ports). The time parameter must be specified, even if it is not included in the block parameters.
-
Sample time inheritance method — definition of the inheritance method of the calculation step
+
Default (by default) | Discrete | Continuous
Details
| The Sample time inheritance method setting disappears from the Advanced tab if the Override sample time inheritance method checkbox is selected in the EngeeFunctionCode source code. In this case, the method of inheritance of the calculation step is determined by the code of the function cell Sample times inheritance method. |
Defines the method of inheritance of the calculation step depending on the selected value:
If the value is specified in the Sample Time field -1, then the calculation step is inherited according to the method specified in the Sample time inheritance method field, depending on the selected value (Default, Discrete, Continuous). In all other cases (Sample Time is not equal to -1 and the SampleTime is greater than or equal to 0) — block Engee Function it works with the specified value of the Sample Time field, ignoring the Sample time inheritance method.
|
-
Default— the default method of inheritance of the calculation step. The method of inheritanceDefaultit is always used when the block Engee Function it is not discrete or continuous. The method gets any kind of calculation step. When choosing this method, the block Engee Function It will inherit the calculation step according to the following principles:-
If the block has no input ports, there is a continuous calculation step at the output.
-
If all the calculation steps are the same at the input, the calculation step at the output is the same as the input.
-
If there are continuous calculation steps among the input steps, there are also continuous calculation steps at the output.
-
If there is a fixed minor (FiM, Fixed-in-Minor) among the input calculation steps, there is no continuous calculation step and solver with variable pitch — the output is a fixed small one.
-
If there is no continuous and fixed number of calculation steps at the input and not all calculation steps are equal, only discrete calculation steps at the input are considered, for which one of the options is valid.:
-
If the largest common divisor of the discrete calculation steps coincides with one of the input calculation steps or a constant—step solver is used, the output is a discrete calculation step with the step of the largest common divisor.
-
If the variable—step solver and the largest common divisor of the input discrete calculation steps do not match any of the input calculation steps, the output is a fixed small one.
-
-
-
Discrete— an inheritance method for obtaining a discrete calculation step. When choosing this method, the block Engee Function It will inherit the calculation step according to the following principles:-
If there are continuous or fixed small calculation steps at the input, the output is a discrete calculation step with a solver step (even if the solver is with a variable step).
-
If there are discrete calculation steps at the input, the output is a discrete calculation step with the largest common divisor from the input discrete calculation steps.
-
-
Continuous— an inheritance method to obtain a continuous calculation step regardless of the input calculation steps.
An example of redefining a function propagate_sample_times with a job similar to the inheritance method Default:
+
function propagate_sample_times(inputs_sample_times::Vector{SampleTime}, fixed_solver::Bool)::SampleTime
nonnegative_sample_times = filter(
st -> st.period >= 0,
collect(values(inputs_sample_times)),
)
finite_periods = filter(
st -> !isinf(st.period),
nonnegative_sample_times,
) .|> (st -> st.period)
output_sample_time = if !isempty(nonnegative_sample_times)
if allequal(nonnegative_sample_times)
first(nonnegative_sample_times)
elseif any(st -> st.period == 0 // 1 && st.mode == :Continuous, nonnegative_sample_times)
(period = 0 // 1, offset = 0 // 1, mode = :Continuous)
elseif any(st -> st.mode == :FiM, nonnegative_sample_times) && !fixed_solver
(period = 0 // 1, offset = 0 // 1, mode = :FiM)
elseif (
all(x -> x.period > 0 // 1, nonnegative_sample_times) &&
(fixed_solver || gcd(finite_periods) in finite_periods)
)
(period = gcd(finite_periods), offset = 0 // 1, mode = :Discrete)
else
(period = 0 // 1, offset = 0 // 1, mode = :FiM)
end
else
(period = 0 // 1, offset = 0 // 1, mode = :Continuous)
end
return output_sample_time
end
If the function propagate_sample_times returns (period = 0 // 1, offset = 0 // 1, mode = :Discrete), then such a calculation step will be perceived as discrete with a solver step.
|
Setting up the parameters
Number of parameters — specify the number of parameters
+
1 (default)
Details
The number of parameters used in the block.
Parameter — defines a parameter as a variable
+
scalar | vector | array
Details
Defines a parameter to use in the block source code Engee Function. In the parameter, you can set:
-
Name— parameter name; -
Value— the value of the parameter. Any Julia expressions can be set as values.
The value and name of the parameter can be changed in the Parameters tab. The name of the first parameter (present by default) — gain, the value of which is 2. The new parameters are called parameter2 and then ascending. The default value of the new parameters is 0.
Global variables available in the Engee variables window ![]() you can set Parameters tabs as variables for insertion into the block source code. Engee Function. If the name of the parameter and the global variable match, the parameter value will be automatically substituted from the global variable.
you can set Parameters tabs as variables for insertion into the block source code. Engee Function. If the name of the parameter and the global variable match, the parameter value will be automatically substituted from the global variable.
To set the bus parameter, set for the parameter Value the bus value in the form of a named tuple, for example (s1 = 5, s2 = 4).
|
It is important to distinguish between the block parameters that are set in the Parameters tab and global variables in the source code. Engee Function, from global variables Engee in the variables window |
Let’s consider the case when global variables fully correspond to variables in the source code. For example, three global variables were set , , with values 1, 2, 3 accordingly. All three global variables are used as block parameters. Engee Function:

Then the source code with the added parameters will look like this:
struct Block <: AbstractCausalComponent
a::Real
b::Real
c::Real
function Block()
new(a_param, b_param, c_param)
end
end
function (c::Block)(t::Real, x::Vector{<:Real})
return (c.a .* x .+ c.b) ./ c.c
endThis source code defines the structure Block, which allows you to customize the behavior of the component. The example uses the names of the block parameters. a_param, b_param, and c_param to set the structure parameters , , and accordingly. The code also defines a method function(c::Block)(t::Real, x::Vector{<:Real}), which scales each element of the vector x to the block parameter , adds and divides the result by . This allows you to flexibly change and normalize the vector. x according to the values of the block parameters.
Let’s consider a case where only the parameters of the Parameters tab are used.:
struct Block <: AbstractCausalComponent end
function (c::Block)(t::Real, x::Vector{<:Real})
return (a_param .* x .+ b_param) ./ c_param
endThese parameters will be global variables in the block code. This means that they will always be available in any part of the block code without having to define them repeatedly in each function or block of code. This greatly simplifies the code and makes it easy to change the parameters in the Parameters tab without affecting the source code.
Let’s consider the case when the parameters do not fully match the source code. For example, there is a parameter a_param, equal to 100. There is a structure field in the source code :
struct Block <: AbstractCausalComponent
a::Real
function Block()
new(a_param/10)
end
end
function (c::Block)(t::Real, x::Vector{<:Real})
c.a
endIn this code, the parameter a_param used to initialize the field structures struct Block through its constructor, which divides the parameter value into 10. In this case, the field is returned in the block’s functor .
Variables can be made global right in the source code.:
a = 1;
b = 2;
c = 3;
struct Block <: AbstractCausalComponent; end
function (c::Block)(t::Real, x::Vector{<:Real})
return (a .* x .+ b) ./ c
endA structure is created in the code Block and a function is defined that performs mathematical operations with global variables. , and by applying them to a variable x.
If you don’t want to use the parameters from the Parameters tab, you can initialize the variables directly in the source code.:
struct Block <: AbstractCausalComponent; end
function (c::Block)(t::Real, x)
a = 1;
b = 2;
c = 3;
return (a .* x .+ b) ./ c
endA structure is created in the code Block and defines a function that performs mathematical operations with local variables. , and by applying them to a variable x.
Let’s consider the most effective and correct way to do it. To block Engee Function it worked correctly, check the box for the option Use external cache for non-scalar output on the Main tab of the block Engee Function. The source code will look like this:
struct Block{Ta, Tb, Tc} <: AbstractCausalComponent
a::Ta
b::Tb
c::Tc
function Block()
Ta = typeof(a_param); Tb = typeof(b_param); Tc = typeof(c_param)
all(isreal, (a_param, b_param, c_param)) ||
error("The block parameters must be real")
all(x->isempty(size(x)), (a_param, b_param, c_param)) ||
error("The block parameters must be scalars.")
new{Ta, Tb, Tc}(a_param, b_param, c_param)
end
end
function (c::Block)(t::Real, cache::Vector{<:Real}, x::Vector{<:Real})
cache .= (c.a .* x .+ c.b) ./ c.c
nothing
end| This code can only be written in a cell. Common code, since the standard cells do not allow editing the definition of the component structure and the signature of the functor. |
Fields , and structures are block parameters that are strictly checked for types in the constructor. Each of these parameters must be a real scalar (Real), which ensures the accuracy of calculations during execution.
Designer Block() checks the types of passed parameters , and . If at least one of them is not a real scalar or has inappropriate dimensions (they must be scalars), the constructor generates an error with the corresponding message. After verification, the constructor initializes the fields of the structure with the values , and the specified types Ta, Tb and Tc.
The calculated function defined for Block instances takes time t, external cache and vector x real numbers. Fields are used in this function , and structures Block to calculate the values, which are then written to the cache. This avoids unnecessary memory allocations by reusing the provided cache.
Thus, the structure Block provides strict management of data types and efficient use of resources by using an external cache to store the results of calculations.
If you want to change the block parameters, you must use mutable the structure. Consider an example:
mutable struct Counter{T} <: AbstractCausalComponent
limit::T
iter::T
function Counter()
isempty(size(limit)) || error("The block limit of $BLOCK_NAME must be a scalar")
isreal(limit) || error("The block limit of $BLOCK_NAME must be a real number")
T = typeof(limit)
iter = zero(T)
new{T}(limit, iter)
end
end
function (c::Counter)(t::Real)
return c.iter
end
function update!(c::Counter, t::Real)
c.iter += 1
if c.iter > c.limit
c.iter = zero(c.iter)
end
c
endStructure Counter — This is mutable the data type that is used to count iterations with a specified limit and is strongly typed. Fields limit and iter The structures represent the block parameters:
-
limit— this is the limit value of the counter; -
iter— the current value of the counter.
The parameter is checked (validated) in the structure constructor. limit whether the parameter is a scalar and a real data type. After that, the field is initialized. iter with a zero value of the corresponding type T. Function update! updates the tag status , increasing the value iter by one for each call. If the current value is iter exceeds limit, then it is reset to zero and allows the counter to cycle back to its initial state.
In the source code of the block Engee Function you can use include, referring to the external code. This allows you to initialize variables from external code (if any) in the source code.
|
| The actual data type, as well as the support for possible data types, depends on the user code inside the block. |
Sample code
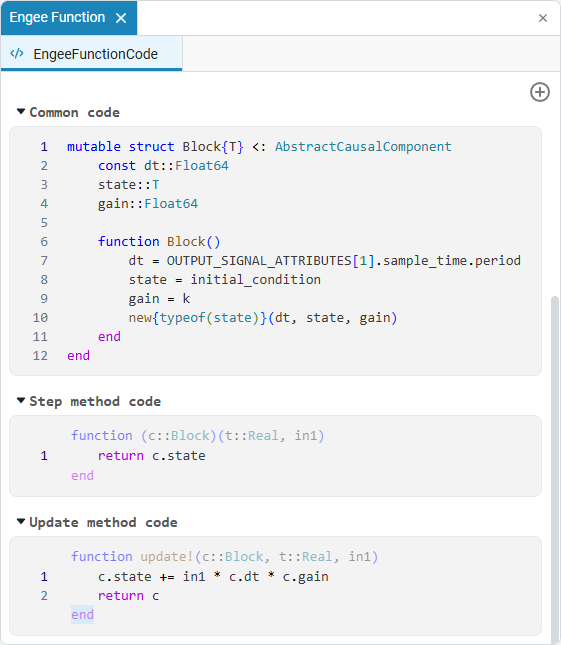
This example shows a simplified implementation of the block. Discrete-Time Integrator, based on the integration of Julia code into the Engee model. The direct Euler method is chosen as the integration method. On the Advanced tab of the block Engee Function set the value Discrete the Sample time inheritance method parameter. Next, fill in the source code cells as follows:
-
In the cell Common code:
mutable struct Block{T} <: AbstractCausalComponent const dt::Float64 state::T gain::Float64 function Block() dt = OUTPUT_SIGNAL_ATTRIBUTES[1].sample_time.period state = initial_condition gain = k new{typeof(state)}(dt, state, gain) end end -
In the cell Step method code:
return c.state -
In the Update method code cell:
c.state += in1 * c.dt * c.gain return c
As a result, the following source code will be obtained:
Parameters initial_condition and k they are initialized in the Parameters tab of the block settings Engee Function:
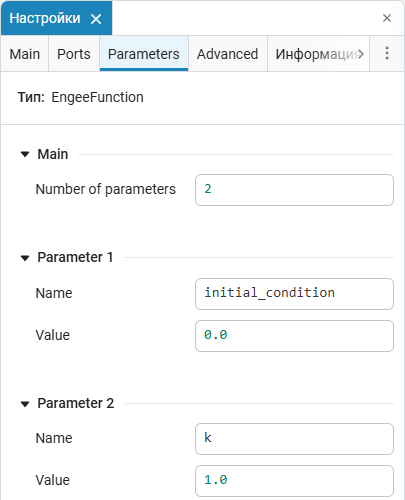
At the first step of the model simulation, the internal state of the block is c.state initialized by the parameter value initial_condition.
After that, at each calculation step, the block returns the internal state. c.state as an output signal and recalculates its value in the method update!.
| The component structure is redefined in the cell Common code, and not in Component struct code, since a more flexible definition is required: the structure must be mutable and parameterized by the type T corresponding to the type of state. The standard definition in Component struct code It is suitable only for immutable and nonparametrized structures. |
Advanced usage
Block Engee Function allows you to set the behavior of a component using your own code, without having to assemble it from ready-made blocks. This makes it possible to manually control the types and dimensions of the output signals, use caching to improve performance, disable direct transfer of inputs to outputs, and set your own data update period.
So, on the page posted in Engee Community by link provides practical examples of advanced usage of the block Engee Function:
-
Converting input data into a vector with redefinition of output parameters;
-
Using caching and strongly typed structures to improve performance;
-
Implementation of blocks without direct feedthrough for breaking algebraic loops;
-
Setting the user sampling period of the output signal.
Annotations
Annotations in Engee Function they allow you to display the block parameters directly under its name in the model. To add them, open settings window ![]() the block Engee Function and go to the Annotation tab. Select the desired block property markers and add them to the text editor.
the block Engee Function and go to the Annotation tab. Select the desired block property markers and add them to the text editor.
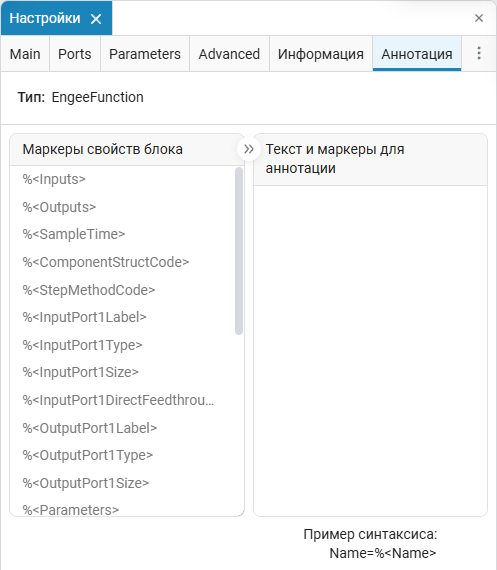
On this tab:
-
A list of available options (except hidden ones) is displayed on the left.
-
On the right is a text editor where you can set an annotation with markers in the format
%<Parameter Name>. -
The parameters can be transferred manually, via auto-completion, or using the button
 .
.
After exiting the editor (for example, when clicking outside of it), the annotation is applied: the markers are automatically replaced with the actual parameter values, and the final text is displayed under the block name (or above it, if the name is placed on top).
To delete annotations, you must delete the corresponding marker in the editor.
Available Markers
The property marker is automatically replaced with the current parameter value. The following markers are available:
-
Ports:
%<Inputs>,%<Outputs>— number of input and output ports;%<InputPort1Type>,%<OutputPort1Type>,%<InputPort1Size>,%<OutputPort1Size>— the type of data and the dimension of the signals. -
Temporary characteristics:
%<SampleTime>— discreteness;%<SampleTimeInheritanceMethod>— the method of inheritance of discreteness. -
Code blocks:
%<ComponentStructCode>,%<StepMethodCode>— the code of the step structure and method. -
Parameters:
%<Parameters>,%<Parameter1Name>,%<Parameter1Value>— names and values of the parameters. -
Enable flags:
%<DefineComponentStruct>,%<UseCommonCode>,%<DefineStepMethod>,%<DefineUpdateMethod>,%<DefineTerminateMethod>— inclusion of the relevant sections of the code. -
Redefinition methods:
%<OverrideTypesInhMethod>,%<OverrideDimsInhMethod>,%<OverrideSampleTimeInhMethod>— type inheritance settings. -
Other:
%<UseExternalCache>— using an external cache.
