Simulation of an electric oscillatory circuit
Introduction
In this example, we will consider modeling an electric oscillatory circuit, as well as using the Engee Function modeling environment block.
Task:
An electrical circuit consisting of an ideal capacitor with a capacity of C = 1 F, an ideal inductor with an inductance of L = 1 Gn and a ground is given. Let's assume that at the initial moment of time the capacitor is charged to 1 V, and there is no current in the circuit.
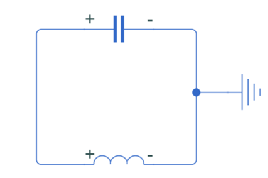
Construct the Cauchy problem corresponding to the electrical circuit for a system of ordinary differential equations and write a program for solving it using any numerical method in the interval t ∈ [0; 100]. Give graphs of changes in capacitor current and voltage. Justify the correctness of the solution obtained both from the point of view of the physics of the process and from the point of view of mathematics.
Calculation algorithm
Solution:
The electrical circuit specified in the assignment corresponds to the differential equation of undamped oscillations in an oscillatory circuit.:
where - voltage across the capacitor, - current strength, a - change in current strength.
Then the equation above takes the form:
In order to lower the order of the derivative, a variable substitution was applied.: . As a result, a system of equations is obtained:
We apply the formula of the Euler method to the resulting system and obtain:
Implementation of the calculation algorithm in Julia language:
Pkg.add(["CSV"])
using Plots # importing a graphics library
n = 1000; # number of calculation steps
U = fill(0.0,n); # defining arrays
Y1 = fill(0.0,n);
Y2 = fill(0.0,n);
t = fill(0.0,n);
U[1] = 1.0; # the voltage of the source at the initial time, at the first step of the calculation
C = 1.0; # capacitor capacity
L = 1.0; # inductance
Y1[1] = 0.0; # current strength
Y2[1] = U[1]/L; # the rate of change in current strength
h = 0.1; # the size of the calculation step
t[1] = 0.0; # time at the first step of the calculation
for i=2:n # the beginning of the cycle
Y2[i] = Y2[i-1] - h * (Y1[i-1] / (L * C));
Y1[i] = Y1[i-1] + h * Y2[i];
U[i] = U[i-1] - h * (Y1[i] / C);# the voltage change obtained from the formula U =q/C, where q is the charge of the capacitor and C is its capacity
t[i] = t[i-1] + h;
end
I = Y1;
Visualization of calculated parameters
Calculation results obtained during the implementation of the model:
plotlyjs()
plot(t, I, xlabel="t", ylabel="", title="Voltage U and current I", linecolor =:blue, bg_inside =:white, line =:solid, label = "I")
plot!(t, U, xlabel="t", ylabel="", title="Voltage U and current I", linecolor =:red, bg_inside =:white, line =:dashdot, label = "U")
Implementing a model launch in Engee using software management
Loading the model:
modelName = "LC_model";
LC_model = modelName in [m.name for m in engee.get_all_models()] ? engee.open( modelName ) : engee.load( "$(@__DIR__)/$(modelName).engee");
Launching the uploaded model:
data = engee.run( modelName )
Downloading and visualizing the data obtained during the simulation
Reading csv files with data on voltage and current changes, followed by conversion to a dataframe and matrix.
using CSV, DataFrames
voltage = data["voltage"];
current = data["current"];
Connecting the library for charting:
using Plots
Plotting a graph describing the voltage change.
plot(voltage.time, voltage.value, xlabel="Time, from", ylabel="The amplitude", title="Voltage U and current I", linecolor =:red, bg_inside =:white, line =:dashdot, label = "U")
plot!(current.time, current.value, xlabel="Time, from", linecolor =:blue, bg_inside =:white, line =:solid, label = "I")
Conclusion
In this example, the calculation of LC circuit oscillations was demonstrated using a script, as well as in a visual modeling environment using the Engee Function block.
As can be seen from the graphs, the oscillations are undamped, since the circuit has only ideal elements that do not take into account energy dissipation. The frequency of the oscillations obtained during the simulation corresponds to the calculated one using the formula and it is 0.1591 Hz, with an oscillation period of 6.28 s.