Engee documentation
Notebook

Numerical solution of the partial derivative equation on the example of an acoustic wave

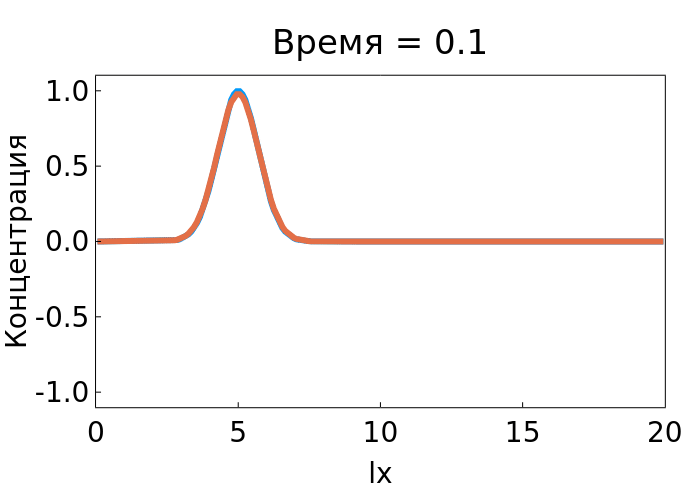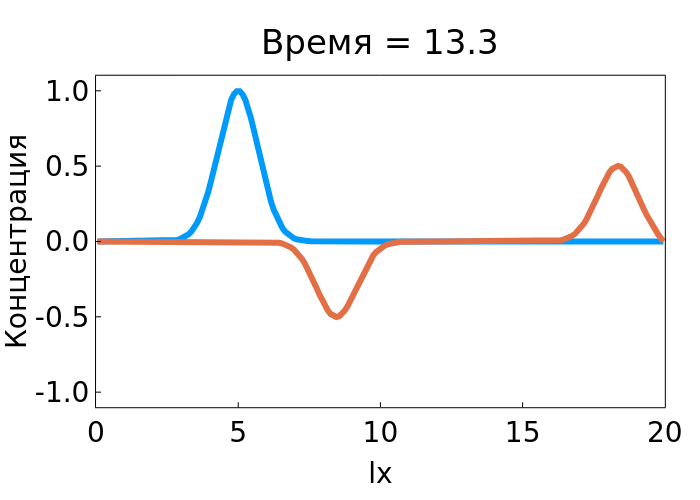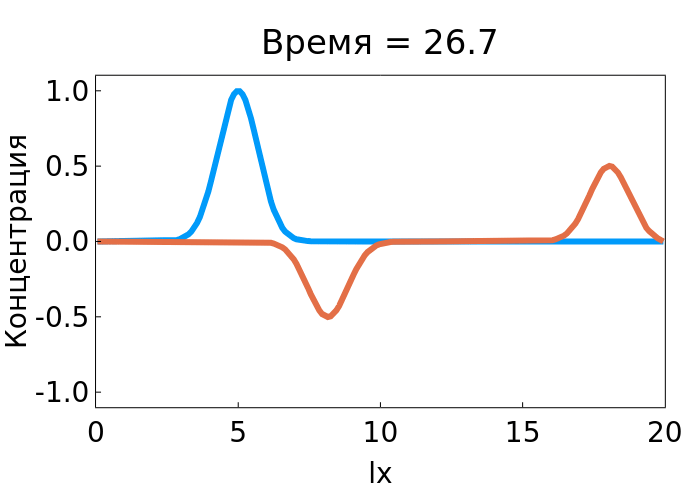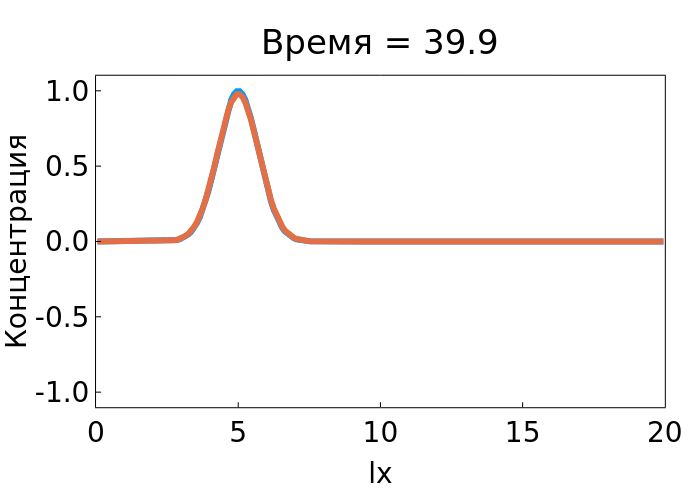
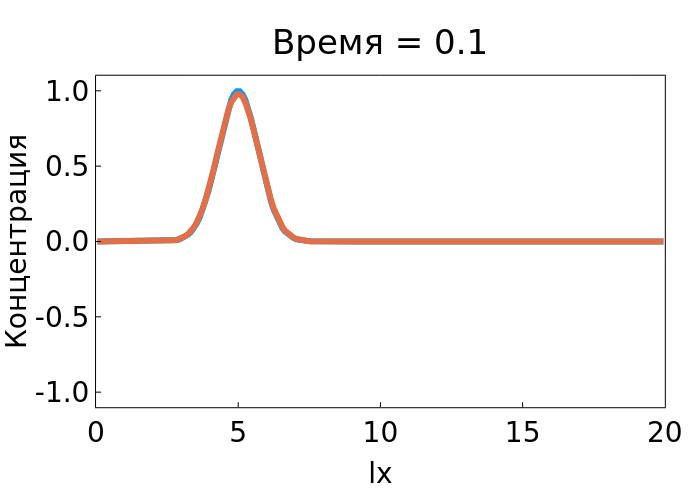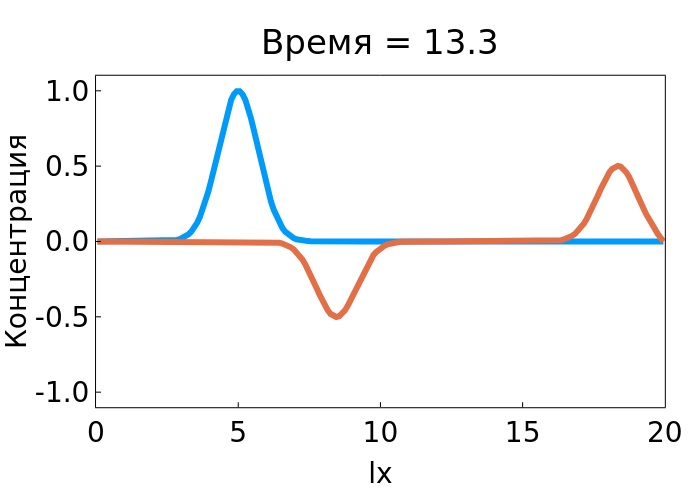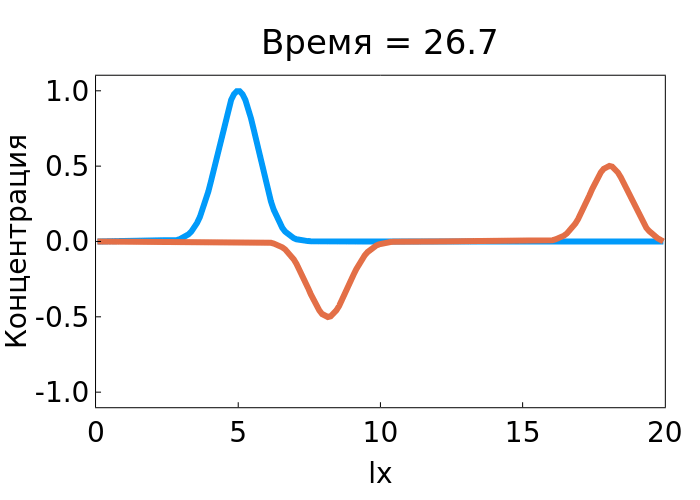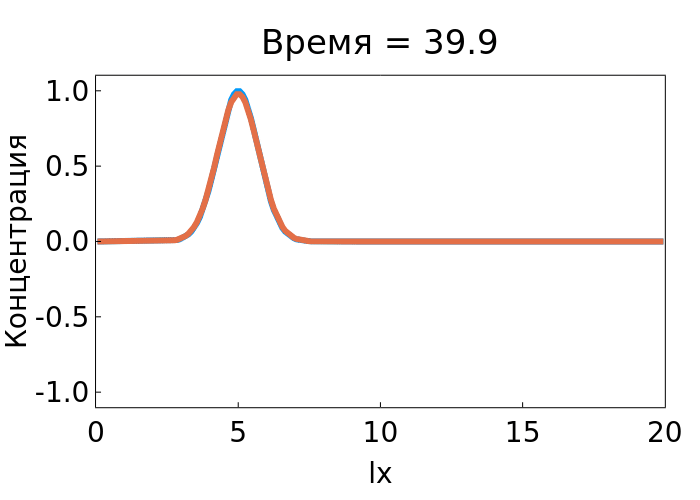
In this example, we will examine the numerical solution of a partial derivative equation using the example of an acoustic wave oscillation. The topic of inline functions will be touched upon to show how to improve the readability of the code without reducing the speed of execution.

We will consider the solution of the string oscillation equation without delving into the code, but only paying attention to its structure. (The code will be explained in the next chapter).

@views function acoustic_wave_1D_orig()
    # physical parameters
    lx = 20.0
    ρ, β = 1.0, 1.0
    # counts
    nx = 200
    nvis = 2
    # differentials
    dx = lx / nx
    dt = dx*√(ρ / β)
    nt = nx^2 ÷ 100
    xc = LinRange(dx / 2, lx - dx / 2, nx)
    # array initialisation
    Pr = @. exp(-(xc - lx / 4)^2)
    Sample = copy(Pr)
    Vx = zeros(Float64, nx - 1)
    # algorithm loop
    @gif for it = 1:nt
            Vx .-= dt ./ ρ .* diff(Pr) ./ dx
            Pr[2:end-1] .-= dt ./ β .* diff(Vx) ./ dx
            plot(xc, [Sample, Pr]; xlims=(0, lx), ylims=(-1.1, 1.1),
                 xlabel="lx", ylabel="Concentration",
                 title="Time = $(round(it*dt,digits=1))")
    end every nvis
end

Несмотря на то, что код сопровождается комментариями, можно явно выделить этапы работы функции. Может возникнуть предположение, что внедрение функций в код под каждый этап замедлит выполнение главной функции.

Действительно, вызов функции занимает значительное время, в сравнении с арифметическими операциями. Однако компиляторы умеют оптимизировать код и делать функции встраиваемыми.

Чтобы проверить, происходит ли вызов функции - воспользуемся макросом @code_llvm, который покажет код, близкий к ассемблеру. (Для большей читабельности можно включить тёмную тему в Engee)

In [ ]: 
function fa(a,b)
   return a+b
end

function fb(a,b,c)
    fa(a,b)*c
end


@code_llvm fb(1,2,4)

;  @ In[1]:5 within `fb`
define i64 @julia_fb_7009(i64 signext %0, i64 signext %1, i64 signext %2) #0 {
top:
;  @ In[1]:6 within `fb`
; ┌ @ In[1]:2 within `fa`
; │┌ @ int.jl:87 within `+`
    %3 = add i64 %1, %0
; └└
; ┌ @ int.jl:88 within `*`
   %4 = mul i64 %3, %2
   ret i64 %4
; └
}

В строчке %3 = add i64 %1, %0 происходит сложение чисел a и b. Для того чтобы явно указать компилятору, что не нужно делать оптимизацию встраивания, воспользуемся макросом @noinline

In [ ]: 
@noinline function fa(a,b)
   return a+b
end

function fb(a,b,c)
    fa(a,b)*c
end

@code_llvm fb(1,2,4)

;  @ In[2]:5 within `fb`
define i64 @julia_fb_7058(i64 signext %0, i64 signext %1, i64 signext %2) #0 {
top:
;  @ In[2]:6 within `fb`
  %3 = call i64 @j_fa_7060(i64 signext %0, i64 signext %1)
; ┌ @ int.jl:88 within `*`
   %4 = mul i64 %3, %2
   ret i64 %4
; └
}

Теперь же происходит вызов функции fa, которая складывает a и b:

%3 = call i64 @j_fa_7789(i64 signext %0, i64 signext %1)

Для того чтобы убедиться в том, что встроенная функция работает быстрее, чем вызываемая - напишем следующий код:

In [ ]: 
@noinline function fa_noinline(a,b)
    a + b
end
@inline function fa_inline(a,b)
    a + b
end

function test_fa_noinline(N)
   sum = 0
   for i in 1:N
    sum += fa_noinline(i,i)   
   end 
   sum
end

function test_fa_inline(N)
   sum = 0
   for i in 1:N
    sum += fa_inline(i,i)   
   end 
   sum   
end
Out[0]:
test_fa_inline (generic function with 1 method)

И подключим библиотеку BenchmarkTools для оценки времени выполнения кода:

In [ ]: 
# import Pkg; Pkg.add("BenchmarkTools")
using BenchmarkTools
N = 10^5
@btime test_fa_noinline($N)

  156.660 μs (0 allocations: 0 bytes)
Out[0]:
10000100000
In [ ]: 
@btime test_fa_inline($N)

  3.161 ns (0 allocations: 0 bytes)
Out[0]:
10000100000

Как видим, встроенная функция работает, быстрее.

Уравнение акустической волны

Уравнение акустической волны имеет вид: $\frac{\partial^2 P}{\partial t^2} = c^2 \frac{\partial^2 P}{\partial x^2}$

где $P$ - давление, $t$ - время, а $x$ - положение частиц в некоторой среде. $c$ - скорость звука в этой среде.

Введём некоторые обозначения:

$c^2 = \frac{1}{\beta \rho}$

$\frac{1}{\beta}$ - объёмный модуль сжимаемости (βulk modulus)

$\rho$ - плотность среды. Тогда исходное уравнение второго порядка: $\frac{\partial^2 P}{\partial t^2} = c^2 \frac{\partial^2 P}{\partial x^2}$ можно переписать как систему двух уравнений первого порядка:

$$\left\{ \begin{array}{cl} \frac{\partial V_x }{\partial t} = -\frac{1}{\rho} \frac{\partial P}{\partial x} \\ \frac{\partial P }{\partial t} = -\frac{1}{\beta} \frac{\partial V_x}{\partial x} \end{array} \right.$$

Numerical solution of the acoustic wave equation

Let us introduce a function specifying the physical parameters of our equation:

In [ ]: 
@doc """
- lx - длина среды, по которой распространяется волна
- ρ  - плотность
- β  - модуль сжимаемости
"""
physical_parameters(;lx = 20, ρ = 1, β = 1) = (lx,ρ,β)
@doc physical_parameters
Out[0]:
  • lx - длина среды, по которой распространяется волна
  • ρ - плотность
  • β - модуль сжимаемости

We set it so as to demonstrate the following scenarios:

In [ ]: 
physical_parameters() # хотим использовать параметры по умолчанию
Out[0]:
(20, 1, 1)
In [ ]: 
physical_parameters(lx=100,β=10) # меняем какие-то параметры, остальные оставляем по умолчанию
Out[0]:
(100, 1, 10)

Note that a tuple is a specific data type that is worth understanding when to apply.

However, for a small set of data that is worth unpacking, a tuple is one of the best options. In the function below foo, we can see that the compiler has seen that "unpacking" a tuple is simply assigning a,b,c to the values x,y and z. And there is no need to make any calls to the elements of the tuple.

In [ ]: 
function foo(x,y,z)

    a,b,c = physical_parameters(;lx = x, ρ=y, β=z)
    return a+b+c
    
end

@code_llvm foo(10,20,30)

;  @ In[9]:1 within `foo`
define i64 @julia_foo_7547(i64 signext %0, i64 signext %1, i64 signext %2) #0 {
top:
;  @ In[9]:4 within `foo`
; ┌ @ operators.jl:587 within `+` @ int.jl:87
   %3 = add i64 %1, %0
   %4 = add i64 %3, %2
; └
  ret i64 %4
}

If physical_parameters returned a vector [lx, ρ, β] instead of the tuple (lx, ρ, β), the assembly code would be much larger and take longer to execute.

Finite element method

To solve the system of equations, we will use the finite difference method in conjunction with Euler's method. (Often the more accurate centre difference is used to solve this type of problem.)

The essence of the method is to represent an equation in partial derivatives, through small but finite differences:

$\frac{\partial V }{\partial t} = \frac{\partial P}{\partial x} \sim \frac{V_{j}^{n+1} - V_{j}^{n}}{ \Delta t } =\frac{P_{j}^{n+1} - P_{j}^{n}}{\Delta x}$

Selecting the sampling step

Having the length of the "string" lx, we can obtain a spatial discretisation by dividing the length by the number of partitions, which we define ourselves.

  • nx - user defined
  • dx = lx / nx - spatial discretisation step
  • $dt = dx/\sqrt{\frac{1}{\beta \rho}}$ - temporal discretisation step. Its choice affects whether the solution will be stable. The values of this step are chosen based on Courant's condition. In our case, the constant is the speed of sound in the medium.
  • nt can be set by the user, or it can depend on the length to always pass at least 1 period
  • xc is a set of grid centres on which the spatial discretisation is performed
In [ ]: 
function differentials(;lx=20,nx=200,β=1,ρ=1)
    dx=lx/nx
    dt=dx*√(β*ρ)
    nt = nx^2 ÷ 100
    xc = LinRange(dx / 2, lx - dx / 2, nx)
    return(dx=dx,dt=dt,nt=nt,xc=xc)
end
Out[0]:
differentials (generic function with 1 method)
array initialisation

Let's set the arrays corresponding to pressure and velocity. We will also save the initial array of pressures for later visualisation.

In [ ]: 
function arrays_initializer(xc,lx,nx)
    Vx = zeros(Float64, nx - 1)
    Pr = @. exp(-(xc - lx / 4)^2)
    Sample = copy(Pr)
    (Vx=Vx, Pr=Pr, Sample=Sample)
end
Out[0]:
arrays_initializer (generic function with 1 method)

Before proceeding to the solution, let's connect the library for visualisation of solution graphs and their animation:

In [ ]: 
# Pkg.add("Plots")
using Plots, Plots.Measures, Printf
# задаём параметры по умолчанию
default(size=(1500, 600), framestyle=:box, label=false, grid=false, margin=10mm, lw=6, labelfontsize=20, tickfontsize=20, titlefontsize=24)

Finite Difference Solution

a = a - 1 ~ a -= 1

Let's rewrite $\frac{\partial V }{\partial t} = \frac{\partial P}{\partial x} \sim \frac{V_{j}^{n+1} - V_{j}^{n}}{ \Delta t } =\frac{P_{j}^{n+1} - P_{j}^{n}}{\Delta x}$

as

$V_x^{n+1} = V_x^n - \frac{1}{\rho} \Delta t (P^{n+1}-P^n)/ \Delta x$

$V_{j}^{n}$ - scalar, showing the value at time $n$ at the point $j$

For more details, see the figure below.

Similarly for the pressure P.

In [ ]: 
function show_acoustic_wave((Vx,Pr,Sample),(dx,dt,nt,xc);nvis=2,ρ=1,β=1,lx=20)
        @gif for it = 1:nt

        Vx .-= dt ./ ρ .* diff(Pr) ./ dx
        Pr[2:end-1] .-= dt ./ β .* diff(Vx) ./ dx

        plot(xc, [Sample, Pr]; xlims=(0, lx), ylims=(-1.1, 1.1),
                xlabel="lx", ylabel="Концентрация",
                title="Время = $(round(it*dt,digits=1))")
    end every nvis
end
Out[0]:
show_acoustic_wave (generic function with 1 method)

Then the final code will have the following form:

In [ ]: 
@views function acoustic_wave_1D()
    lx, ρ, b = physical_parameters()  # если мы знаем порядок элементов в кортеже
    nx = 200                          # количество ячеек в сетке
    ds = differentials()              # если не знаем, то используем именованный
    dx = ds.dx
    dt = ds.dt
    nt = ds.nt
    xc = ds.xc
    ars = arrays_initializer(xc,lx,nx)
    show_acoustic_wave(ars,ds,nvis=2)
end

@time acoustic_wave_1D()

 12.091866 seconds (2.74 M allocations: 334.784 MiB, 0.59% gc time)

[ Info: Saved animation to /user/start/examples/math_and_optimization/pde_acoustic_wave/tmp.gif
Out[0]:
No description has been provided for this image

Let's compare the execution time with our source code.

In [ ]: 
@views function acoustic_wave_1D_orig()
    # физический параметры
    lx = 20.0
    ρ, β = 1.0, 1.0
    # отсчёты
    nx = 200
    nvis = 2
    # дифференциалы
    dx = lx / nx
    dt = dx*√(ρ / β)
    nt = nx^2 ÷ 100
    xc = LinRange(dx / 2, lx - dx / 2, nx)
    # инициализация массивов
    Pr = @. exp(-(xc - lx / 4)^2)
    Sample = copy(Pr)
    Vx = zeros(Float64, nx - 1)
    # цикл работы алгоритма
    @gif for it = 1:nt
        Vx .-= dt ./ ρ .* diff(Pr) ./ dx
        Pr[2:end-1] .-= dt ./ β .* diff(Vx) ./ dx
            plot(xc, [Sample, Pr]; xlims=(0, lx), ylims=(-1.1, 1.1),
                xlabel="lx", ylabel="Концентрация",
                title="Время = $(round(it*dt,digits=1))")
    end every nvis
end
@time acoustic_wave_1D_orig()

 13.480746 seconds (2.74 M allocations: 334.462 MiB, 0.89% gc time)

[ Info: Saved animation to /user/start/examples/math_and_optimization/pde_acoustic_wave/tmp.gif
Out[0]:
No description has been provided for this image

From this we can conclude that wrapping a small code in a function does not significantly affect its execution speed. However, we may note the following advantages of splitting code into functions:

  1. Documentation of functions. Documenting functions is a much more efficient and expressive tool than commenting code.
  2. Some functions can be used by you in different scenarios
  3. Creating functions allows you to decompose complex tasks into simple ones, and gradually increase the complexity and accuracy of your programme. (Let's insert a simple function first, but check that it works, and then we'll find more precise and efficient ways to implement it)