Simulation of heat propagation in a semi-infinite plate

This example demonstrates the simulation of heat propagation in a two-dimensional semi-infinite plate.

The heat transfer process is generally described by the equation:

Using the Euler method, to calculate the heat propagation in a semi-infinite plate, the equation was transformed into a difference form.:

The equation describes the process of heat transfer in a two-dimensional medium. It simulates the temperature change at spatial points (in two spatial coordinates X and Y and one time coordinate) as a result of heat transfer between them.

Connecting libraries:

using Plots

Determining the source data:

c = 903.7
m = 0.003375
A = 235.9
F = 0.00025
d = 0.01
L = 0.14
q = 1400.0
h = 0.1

0.1

Determining the initial conditions

T0 = 293.15 # the initial temperature of the plate
Ny = 20 # number of points on the Y axis
Nx = 20 # number of points on the X-axis
Nt = 3000 # number of time steps
T = fill(T0, (Nt, Nx, Ny)); # temperature for each element

Setting boundary conditions:

T[:, end, :] .= 293.15; # Ambient temperature on the right (x = L)

Calculation of temperatures and heat flows:

@time for i in 1:Nt-1 # number of time steps
    for k in 1:Ny # cycle along the Y coordinate
        for j in 2:Nx-1 # cycle along the X coordinate
            # Temperature update
            T[i + 1, j, k] = T[i, j, k] + h * (
                (1 / (c * m)) * (
                    A * F * (T[i, j - 1, k] - T[i, j, k]) / d + # heat flow from the left segment
                    A * F * (T[i, j + 1, k] - T[i, j, k]) / d + # heat flow from the right segment
                    (k > 1 ? A * F * (T[i, j, k - 1] - T[i, j, k]) / d : 0) + # heat transfer from the element above
                    (k < Ny ? A * F * (T[i, j, k + 1] - T[i, j, k]) / d : 0) # heat transfer from the element below
                )
            )
            # determination of a permanent heat source
            if T[i+1, 5, 1] < 350.0
                T[i+1, 1:20, 1] = T[i+1, 1:20, 1] .+ 0.05 # heat source
            else
                T[i+1, 1:20, 1] .= 350.0
            end
        end
    end
end

  2.725339 seconds (35.28 M allocations: 648.548 MiB, 17.04% gc time)

Creating animations:

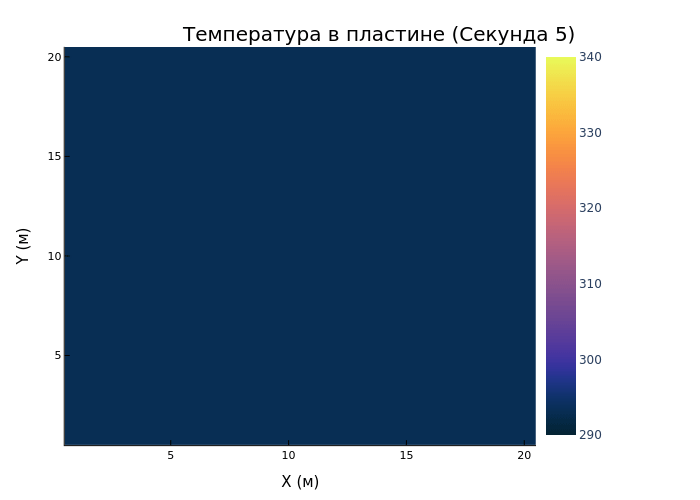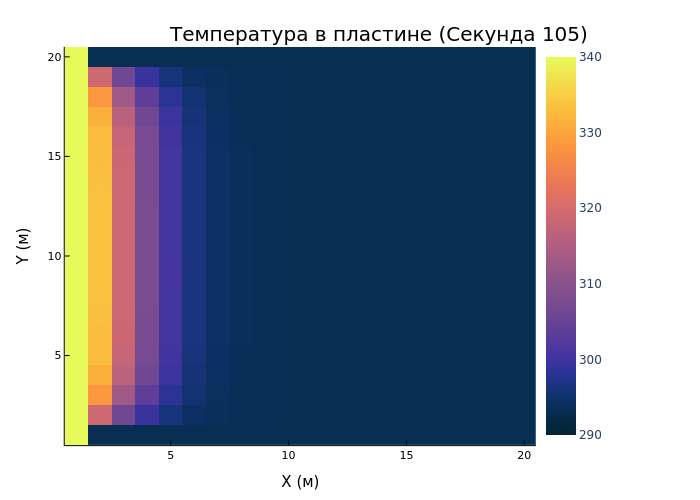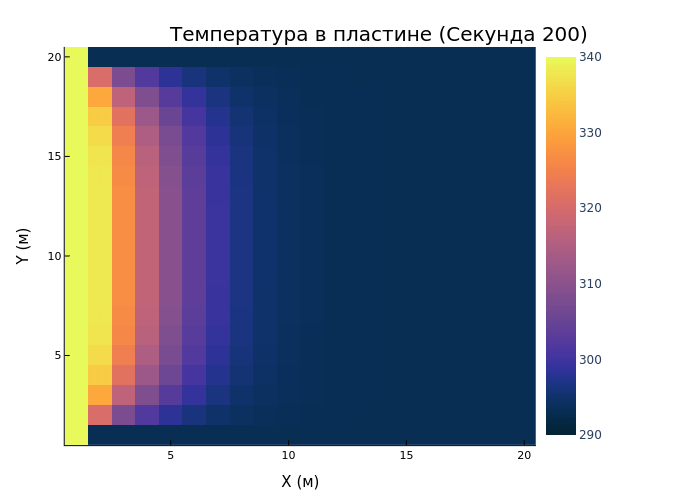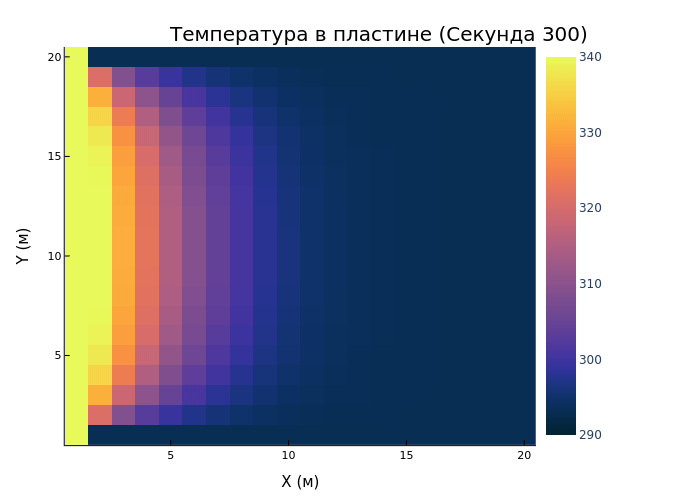
@time anim = @animate (for i in 1:Int(Nt / 50)
    heatmap((T[i, :, :]), color=:thermal, title="Temperature in the plate (Second $(i*5))", xlabel="X (m)", ylabel="Y (m)", size=(400, 400), clims=(290, 340))
end)

  5.687819 seconds (1.56 M allocations: 113.666 MiB, 0.50% gc time, 1 lock conflict)

Animation("/tmp/jl_PVeZHL", ["000001.png", "000002.png", "000003.png", "000004.png", "000005.png", "000006.png", "000007.png", "000008.png", "000009.png", "000010.png"  …  "000051.png", "000052.png", "000053.png", "000054.png", "000055.png", "000056.png", "000057.png", "000058.png", "000059.png", "000060.png"])

Saving animations in GIF:

gif(anim, "heat_distribution_plate.gif", fps=10)

[ Info: Saved animation to /user/heat_distribution_plate.gif