Calculation of the stationary thermal field in detail: Julia, Gmsh, Gridap, VTK and Makie

Let's apply a chain of tools that allows Engee to design, parameterize a model, apply a computational grid to it, build a problem for solving using the finite element method and, as a result, calculate heat transfer in a complex part.

Introduction

For problems requiring precise solutions of partial differential equations (for example, heat transfer or deformable body mechanics), specialized tools (such as Gridap or FEniCS) provide more accurate and flexible results. They allow you to work with arbitrary grids and complex boundary conditions, which is critical for scientific calculations.

Pkg.add(["Gridap", "GridapGmsh", "CairoMakie", "WriteVTK", "ReadVTK", "GeometryBasics"])

For this example, we use a library, the installation of which automatically adds the Gmsh package to the system.

using GridapGmsh

Let's take a simple model example from the repository of this library and slightly modify it:

region boundary 1 will unite the inner surface of the wider hole (on the right)
region boundary 2 - the entire inner surface of the hole with a protrusion (on the left)

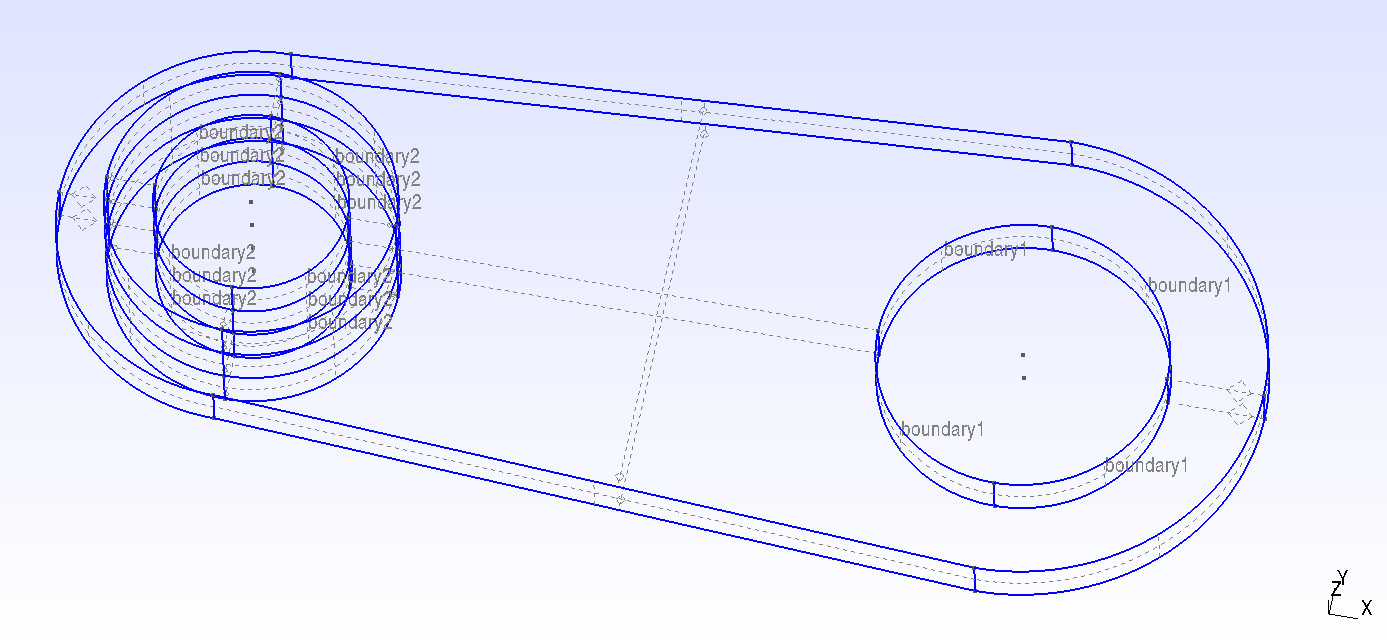
You can create such a parameterized model in a text editor, for example, by visualizing the results in https://gmsh.info / or in one of the many CAD systems for solid-state modeling, including open source ones: [OpenCascade](https://dev.opencascade.org /), [OpenSCAD](https://openscad.org /) and [FreeCAD](https://www.freecad.org /).

Let's upload an example in the * format.geo* (the basic format for geometry in Gmsh) and create a grid:

GridapGmsh.gmsh.initialize()
GridapGmsh.gmsh.clear()
GridapGmsh.gmsh.open("$(@__DIR__)/demo.geo");
GridapGmsh.gmsh.model.geo.synchronize();
GridapGmsh.gmsh.option.setNumber("Mesh.CharacteristicLengthMin", 0.01)  # минимальный размер
GridapGmsh.gmsh.option.setNumber("Mesh.CharacteristicLengthMax", 0.05)  # максимальный размер
GridapGmsh.gmsh.model.mesh.generate(3);
GridapGmsh.gmsh.write("demo.msh");

Let's print the model of our part, which is a set of tetrahedra (Makie does not allow working with tetrahedra, so we manually converted them into triangles). The color scheme of the graph corresponds to the coordinate of the points on the X-axis.

using Gridap, GridapGmsh, GeometryBasics

import CairoMakie: mesh, NoShading
# import WGLMakie: mesh, NoShading # На замену CairoMakie - для интерактивных графиков

model = GmshDiscreteModel("demo.msh");

grid = get_grid(get_triangulation(model))
points = reinterpret(reshape, Float64, grid.node_coordinates)
cells = hcat(grid.cell_node_ids...)

tetrahedra = [ (c[1], c[2], c[3], c[4]) for c in eachcol(cells) ]
all_faces = [ [TriangleFace{Int}(ta, tb, tc),TriangleFace{Int}(ta, tb, td),TriangleFace{Int}(ta, tc, td),TriangleFace{Int}(tb, tc, td)] for (ta, tb, tc, td) in tetrahedra ]
all_faces = reshape(reinterpret(Int, vcat(all_faces...)), 3, :)
colors = points[1,:]

mesh(points', all_faces', color=colors, shading=NoShading)

Info    : Reading 'demo.msh'...
Info    : 188 entities
Info    : 3302 nodes
Info    : 12065 elements
Info    : Done reading 'demo.msh'

Warning : Gmsh has aleady been initialized

Setting a numerical problem

We use the code from basic example for GridapGmsh, where the Laplace's equation is solved with Dirichlet boundary conditions in a weak (variational) formulation by the finite element method (FEM).

Laplace equation and boundary conditions: The function is being searched for satisfying the equation in the area of with boundary conditions on , on , where — the area defined by the grid demo.msh, and — borders with tags "boundary1" and "boundary2" respectively.

Weak form (variational formulation of the problem) is a key method for modern FEM, it weakens the requirements for the smoothness of the solution, and boundary conditions can be set directly without approximating them. And, of course, this is the main method of discretization of the problem, which allows you to set it in basic functions and solve it as a linear system. . So, our problem in the variational formulation is transformed into , where — gradient, — the area of integration, — a test space that turns to zero at the borders.

Note how close the description given in the code is ∫( ∇(v)⋅∇(u) )dΩ towards the Laplace equation in a variational formulation .

using Gridap

model = GmshDiscreteModel("demo.msh");         # Загружаем геометрию сетки из файла *.msh
order = 1
reffe = ReferenceFE(lagrangian,Float64,order)  # Линейные лагранжевы элементы 1-го порядка
V = TestFESpace(model,reffe,dirichlet_tags=["boundary1","boundary2"]) # Пробное пространство
U = TrialFESpace(V,[0,1])                      # Определение пространства решений
                                               # - на boundary1 значение решения u = 0
                                               # - на boundary2 значение u = 1
Ω = Triangulation(model)                       # Триангуляция и мера интегрирования
dΩ = Measure(Ω,2*order)
a(u,v) = ∫( ∇(v)⋅∇(u) )dΩ                      # Слабая форма уравнения Лапласа
l(v) = 0                                       # Линейная форма (правая часть)
op = AffineFEOperator(a,l,U,V)                 # Собираем линейный оператор задачи
uh = solve(op)                                 # Решение системы

writevtk(Ω,"demo",cellfields=["uh"=>uh]);

Info    : Reading 'demo.msh'...
Info    : 188 entities
Info    : 3302 nodes
Info    : 12065 elements
Info    : Done reading 'demo.msh'

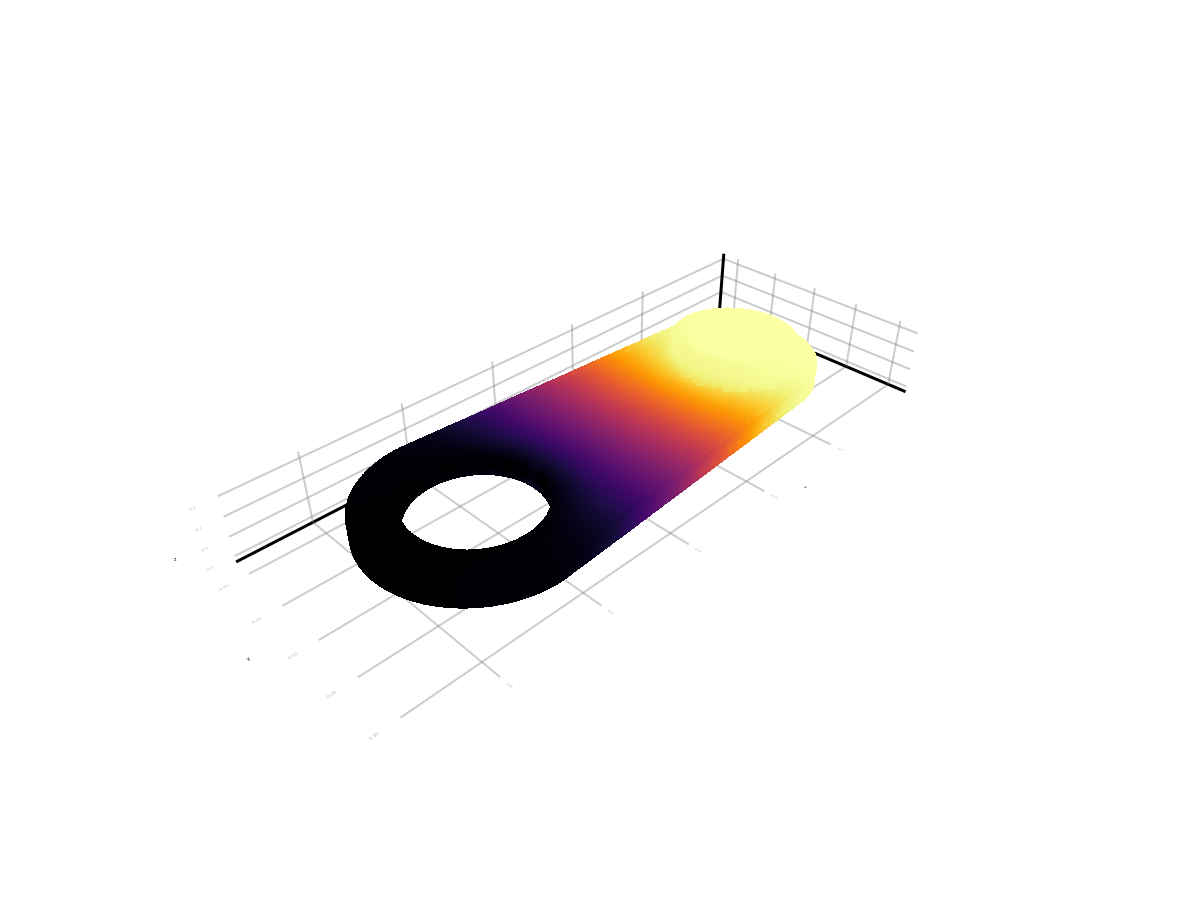
We will go a little further and, in addition to on-the-fly visualization, we will show you how to visualize a calculation saved in VTK. But first, let's show the solution we just improved.:

using GeometryBasics
nodes = GridapGmsh.get_node_coordinates(Ω)
cell_node_ids = GridapGmsh.get_cell_node_ids(Ω)
uh_values = [uh(node) for node in nodes]
points = [Point3f(x...) for x in nodes]
faces = [TriangleFace(cell_node_ids[i][1], cell_node_ids[i][2], cell_node_ids[i][3]) for i in 1:length(cell_node_ids)]
mesh(points, faces, color=uh_values, colormap=:inferno, shading=NoShading)

Visualization of the solution from a VTK file

The most convenient solution for viewing VTK files is an open source program [ParaView](https://www.paraview.org /). But it is also valuable for us to have interactive reports that are fully open in Engee. Therefore, we will open this file in Julia and output the solution directly in this script.

If we run this part asynchronously with the solution of the problem (which may take a long time), we will need to connect these libraries.:

using WriteVTK, ReadVTK

They will help us read the VTK file and display it on 3D graphics. There are additional libraries for some of the functions, but for now we'll make do with low-level commands.:

create a matrix points for the coordinates of the vertices
get the vector uh_values where the field values will be located uh our solution
let's break the tetrahedra cells on a set of triangles all_faces

vtk = VTKFile("demo.vtu")
points = get_points(vtk)
uh_values = get_data(get_point_data(vtk)["uh"])

cells = get_cells(vtk)

# Разобьем массив cells.connectivity на тетраедры, а затем на треугольники
using GeometryBasics
all_faces = TriangleFace{Int}[]
offset = 1
while offset <= length(cells.connectivity)
    ta, tb, tc, td = cells.connectivity[offset:offset+3]
    push!(all_faces, TriangleFace(ta, tb, tc))  # грань 1
    push!(all_faces, TriangleFace(ta, tb, td))  # грань 2
    push!(all_faces, TriangleFace(ta, tc, td))  # грань 3
    push!(all_faces, TriangleFace(tb, tc, td))  # грань 4
    offset += 4
end

# CairoMakie не принимает последний треугольник в модели, временно используем [1:end-1]
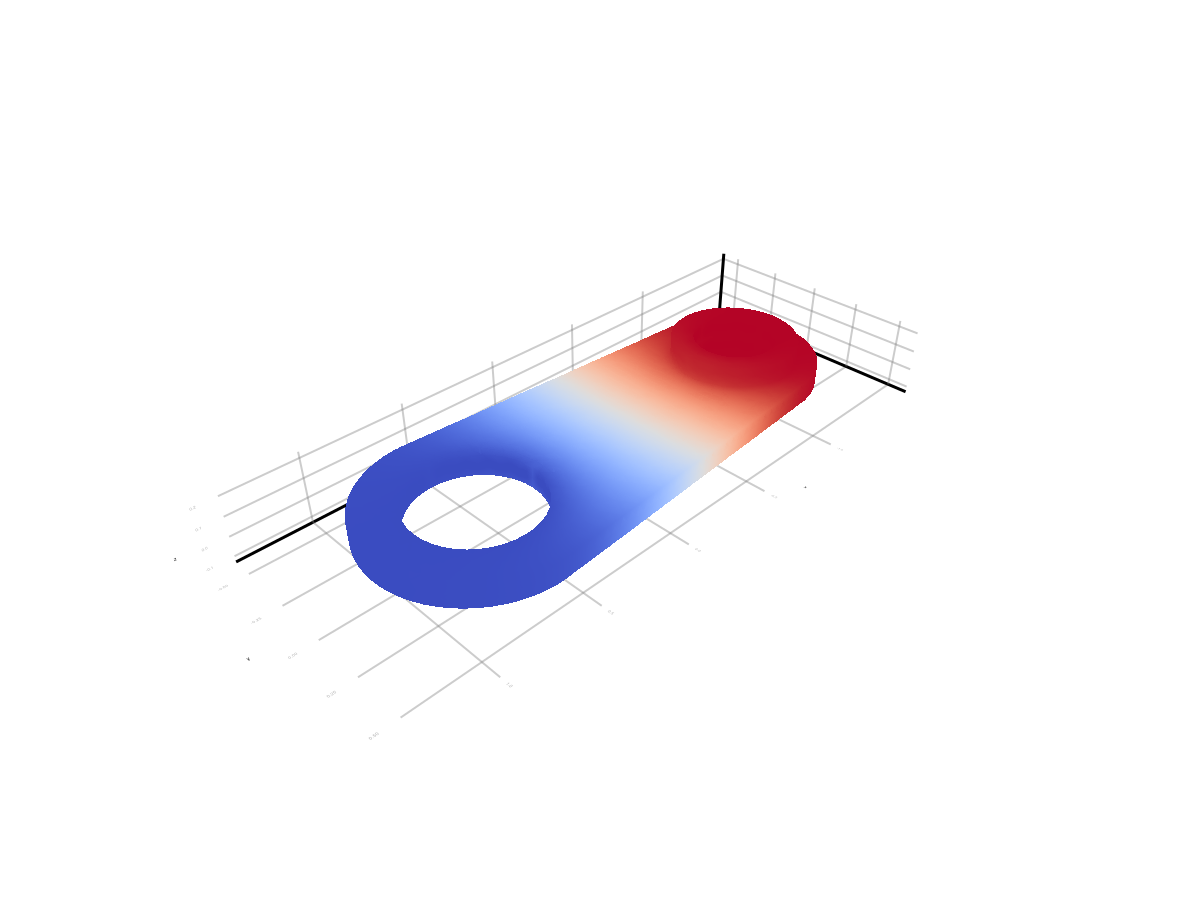
mesh(points, all_faces[1:end-1], color=uh_values, colormap=:coolwarm, shading=NoShading)

Conclusion

We implemented the solution of the Laplace equation on a tetrahedral grid, saved the results in VTK format and visualized them.

These are the key stages of modeling physical fields (thermal, electrical, mechanical). This approach ensures reproducibility, accuracy, and readiness to scale to real engineering tasks that require detailed calculations rather than simplified system approximations.