Engee documentation
Notebook

Simulation of a drone flying over a 3D landscape

The presented Julia code implements a simulation of an unmanned aerial vehicle (UAV) flying over a generated 3D landscape. The program includes several key stages.

  1. Landscape generation using trigonometric functions and random noise to create realistic terrain.
  2. Simulation of drone movement based on height, speed, and obstacle detection limits.
  3. Visualization of the trajectory in 2D and 3D, as well as flight animation based on the detected obstacles.

The code demonstrates the use of numerical methods, linear algebra, and interactive graphics in Julia, which makes it useful for autonomous navigation, robotics, and terrain analysis tasks.

Auxiliary libraries

Add auxiliary objects and libraries.

LinearAlgebra connects a built-in library for linear algebraic operations (matrices, vectors, decompositions, norms, etc.).

plotlyjs() activates the PlotlyJS backend for interactive visualization.

In [ ]: 
using LinearAlgebra
plotlyjs()
Out[0]:
Plots.PlotlyJSBackend()

Three-dimensional landscape generation

Function generate_landscape generates a 3D landscape of specified dimensions (width_m × length_m) and renders it as an interactive surface.

  1. The function creates a grid of coordinates: x and y are linear ranges from 0 to width_m and length_m in increments of 1 meter.
  2. Next, she fills in the heights (z) — uses a combination of sine and cosine to create a hilly surface.
  3. And also adds random noise (rand()) for realism.
  4. In addition, the function determines the random start and finish points of the drone. (green — start, red — finish)

Key parameters

Parameter Type/Value Description
width_m Int The width of the landscape (meters).
length_m Int The length of the landscape (meters).
c=:terrain Symbol Color map for the relief.
start/finish Vector{Float64} Coordinates [x, y, z].
In [ ]: 
function generate_landscape(width_m, length_m)
    x = 0:1:width_m
    y = 0:1:length_m

    z = [10(sin(xi / 15) + cos(yi / 15)) + 5rand() + 10 for xi in x, yi in y]
    z = reverse(z, dims=(1, 2))

    random_yi_start = rand(1:length(y))
    random_yi_finish = rand(1:length(y))
    xi_start = 10
    xi_finish = length(x)-10
    start = [x[xi_start], y[random_yi_start], z[xi_start, random_yi_start]]
    finish = [x[xi_finish], y[random_yi_finish], z[xi_finish, random_yi_finish]]

    plt = surface(x, y, z', c=:terrain, xlabel="X (м)", ylabel="Y (м)", zlabel="Z (м)", title="3D ландшафт", legend=false)
    scatter!(plt, [start[1]], [start[2]], [start[3]+3], marker=(:circle), color=:green)
    scatter!(plt, [finish[1]], [finish[2]], [finish[3]+3], marker=(:circle), color=:red)

    display(plt)
    return x, y, z, start, finish
end

landscape = generate_landscape(100, 100);

Simulation of drone behavior

Algorithm of drone behavior in simulation

1. The basic logic of movement

The drone is moving from the starting point (start) to the finish line (finish) along a straight trajectory, observing the restrictions:

  • Speed: The drone moves a fixed distance (speed) per step.
  • height: maintains a height of at least min_height above the terrain and not higher max_height.
  • border correction: does not fly out of the landscape (clamp).

2. Obstacle detection

The drone scans the space in field of view (FOV) 45° from a preset distance (view_distance):

  • checks the points in the field of view (12 beams).
  • if the height of the obstacle (obstacle_height) threatens with a collision (obstacle_height + min_height > текущая высота), adds it to the list visible_obstacles.

3. Avoiding obstacles
When obstacles are detected, there are the following options.

  • Option 1 (50% chance): shifts sideways (left/right by speed).
  • Option 2 (50% chance): rises above the maximum height of the obstacle + min_height + 1.0.

4. Boarding

Upon reaching the finish line

  • smoothly descends in 10 steps to the height of the relief at the end point.

5. Visualization

  • Graph 1: 2D trajectory (XY) with start (green) and finish (red) marks.
  • Graph 2: step-by-step change in height (Z).

Key parameters

Parameter Value Description
min_height -5 m Minimum height above the terrain
max_height 5 m Maximum flight altitude
speed 1 m/step The speed of movement
fov_angle 45° Viewing angle for detecting obstacles
view_distance 10 m Scanning range
In [ ]: 
function simulate_drone(landscape, min_height, max_height, speed; fov_angle=45.0, view_distance=10.0)
    x, y, z, start, finish = landscape
    drone_path = [copy(start)]
    drone_heights = [start[3]]
    obstacles = [[]]

    current_pos = copy(start)
    for _ in 1:1000
        if norm(current_pos[1:2] .- finish[1:2]) < speed
            break
        end
        direction = normalize(finish[1:2] .- current_pos[1:2])
        next_pos = current_pos[1:2] .+ direction * speed
        next_pos[1] = clamp(next_pos[1], x[1], x[end])
        next_pos[2] = clamp(next_pos[2], y[1], y[end])

        xi = argmin(abs.(x .- next_pos[1]))
        yi = argmin(abs.(y .- next_pos[2]))
        terrain_height = z[xi, yi]
        new_z = clamp(max(terrain_height + min_height, current_pos[3]), -Inf, max_height)

        visible_obstacles = Tuple{Float64, Float64, Float64}[]
        for angle in range(-fov_angle/2, fov_angle/2, length=12)
            rad = deg2rad(angle)
            dir = [direction[1]*cos(rad) - direction[2]*sin(rad),
                   direction[1]*sin(rad) + direction[2]*cos(rad)]
            check_pos = next_pos .+ dir * view_distance
            xi_check = argmin(abs.(x .- check_pos[1]))
            yi_check = argmin(abs.(y .- check_pos[2]))

            if 1 ≤ xi_check ≤ size(z, 1) && 1 ≤ yi_check ≤ size(z, 2)
                obstacle_height = z[xi_check, yi_check]
                if obstacle_height + min_height > new_z
                    push!(visible_obstacles, (x[xi_check], y[yi_check], obstacle_height))
                end
            end
        end

        if !isempty(visible_obstacles)
            max_obstacle = maximum(obs[3] for obs in visible_obstacles)
            if max_obstacle + min_height > new_z
                if rand() < 0.5
                    next_pos[1] = clamp(next_pos[1] + rand([-1.0, 1.0]) * speed, x[1], x[end])
                else
                    new_z = max_obstacle + min_height + 1.0
                end
            end
        end

        current_pos = [next_pos[1], next_pos[2], new_z]
        push!(drone_path, copy(current_pos))
        push!(drone_heights, new_z)
        push!(obstacles, visible_obstacles)
    end

    xi_end = argmin(abs.(x .- finish[1]))
    yi_end = argmin(abs.(y .- finish[2]))
    final_ground = z[xi_end, yi_end]

    for _ in 1:10
        new_z = drone_path[end][3] - (drone_path[end][3] - final_ground) / 10
        push!(drone_path, [finish[1], finish[2], new_z])
        push!(drone_heights, new_z)
        push!(obstacles, [])
    end

    println("Время полёта дрона: $(length(drone_path)) шагов")
    return drone_path, drone_heights, obstacles, start, finish
end

speed = 1
drone_path, drone_heights, obstacles, start, finish = simulate_drone(landscape, -5, 5, speed)

path_x = [p[1] for p in drone_path]
path_y = [p[2] for p in drone_path]
path_z = [p[3] for p in drone_path]
t = 1:length(drone_path)

plt1 = plot(path_x, path_y, lw=2, c=:blue, xlabel="X (м)", ylabel="Y (м)", title="Путь дрона", legend=false)
scatter!(plt1, [path_x[1]], [path_y[1]], marker=:circle, markersize=8, color=:green)
scatter!(plt1, [path_x[end]], [path_y[end]], marker=:circle, markersize=8, color=:red)

plt2 = plot(t, path_z, lw=2, c=:purple, xlabel="Шаги", ylabel="Высота (м)", title="Высоты дрона", legend=false)
scatter!(plt2, [t[1]], [path_z[1]], marker=:circle, markersize=8, color=:green)
scatter!(plt2, [t[end]], [path_z[end]], marker=:circle, markersize=8, color=:red)

plot(plt1, plt2, layout=(1, 2), size=(1000, 400))

Время полёта дрона: 109 шагов
Out[0]:

3. Visualization of drone flight

Drone flight visualization algorithm

1. Setting up Graphics

  • Backend: in use gr() for high-performance rendering.
  • Frame rate: default fps=10 (it is regulated by the parameter).

2. Data preparation

  • Landscape: division into coordinates x, y and heights z.
  • Optimization: dictionaries are created xidx, yidx to quickly search for drone coordinate indexes in the landscape grid.

3. Basic charts

  • 3D surface (base_surface):
  • color scheme :terrain.
    • start (green) and finish marks (red).
  • 2D map (base_2d):
  • contour relief graph (contour!) with transparency alpha=0.3.
    • start and finish points.

4. Flight animation

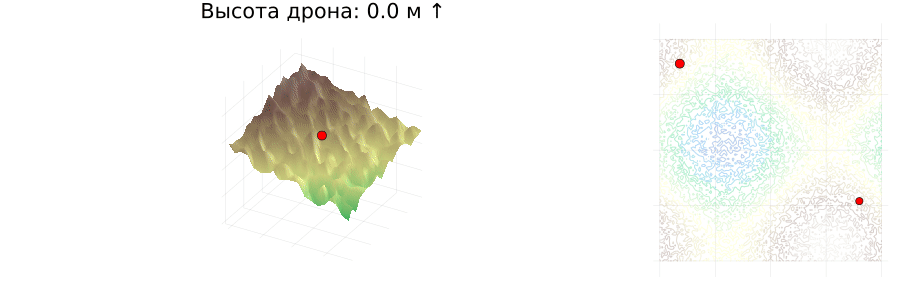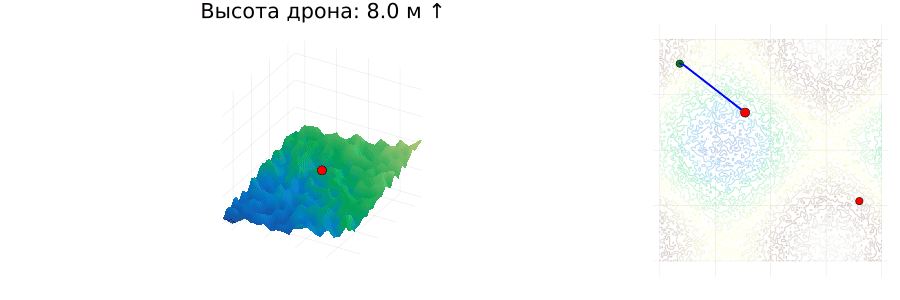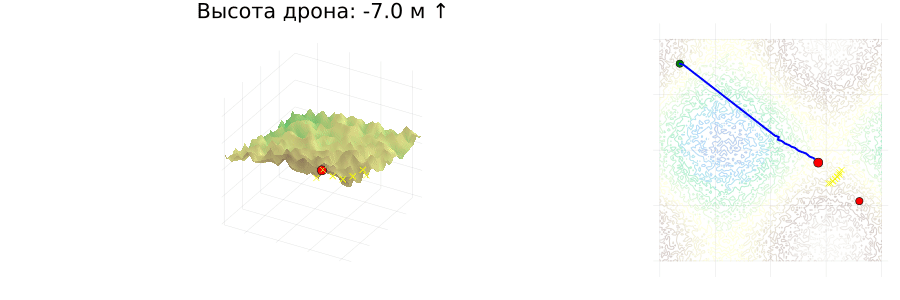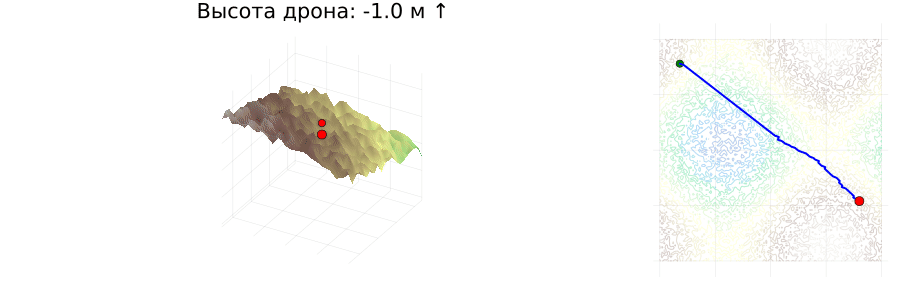
For each frame (i-the th step of the path):

  1. 3D visualization:
  • current drone position (red dot),
  • dynamic borders (xlims!, ylims!) to focus on the area around the drone,
    • a header with a height above the relief and an arrow (↑/↓) indicating a height gain/decrease.
  1. 2D visualization:
  • gradual display of the traveled path (blue line),
  • current position (red dot).
  1. Obstacles:
  • marked with yellow crosses (:xcross) in 3D and 2D, if detected at the current step.

5. Assembling animations

  • frames are generated at intervals 1/speed (but at least 1 step),
  • the resulting animation is saved as a GIF with the specified fps.

Key parameters

Parameter Value/Type Description
fps 10 (default) Animation frame rate (frames/seconds)
speed 1 (m/step) The speed of the drone affects the smoothness of the animation
layout @layout([a{0.7w} b]) Size ratio of 3D and 2D graphs (70% / 30%)
In [ ]: 
gr()

function visualize_flight(landscape, drone_path, drone_heights, obstacles, speed, start, finish; fps=10)
    x, y, z = landscape

    xidx = Dict(px => argmin(abs.(x .- px)) for px in unique(p[1] for p in drone_path))
    yidx = Dict(py => argmin(abs.(y .- py)) for py in unique(p[2] for p in drone_path))

    base_surface = surface(x, y, z', c=:terrain, legend=false, aspect_ratio=:auto, axis=false)
    base_2d = plot(aspect_ratio=1, legend=false, axis=false)
    contour!(base_2d, x, y, z', c=:terrain, alpha=0.3)
    scatter!(base_surface, [start[1]], [start[2]], [start[3]], marker=:circle, markercolor=:green, label=false)
    scatter!(base_surface, [finish[1]], [finish[2]], [z[end, end]], marker=:circle, markercolor=:red, label=false)
    scatter!(base_2d, [start[1]], [start[2]], marker=:circle, markercolor=:green)
    scatter!(base_2d, [finish[1]], [finish[2]], marker=:circle, markercolor=:red)

    anim = @animate for i in 1:length(drone_path)
        plt1 = deepcopy(base_surface)
        plt2 = deepcopy(base_2d)

        px, py, pz = drone_path[i]
        scatter!(plt1, [px], [py], [pz], markersize=5, markercolor=:red, marker=:circle)
        xlims!(plt1, px - 10, px + 10)
        ylims!(plt1, py - 10, py + 10)

        xi, yi = xidx[px], yidx[py]
        height_above = pz - z[xi, yi]
        arrow = i == 1 ? "↑" : (height_above > (drone_path[i - 1][3] - z[xidx[drone_path[i - 1][1]], yidx[drone_path[i - 1][2]]]) ? "↑" : "↓")
        title!(plt1, "Высота дрона: $(floor(height_above)) м $arrow")

        if i > 1
            path = drone_path[1:i]
            plot!(plt2, [p[1] for p in path], [p[2] for p in path], linewidth=2, linecolor=:blue)
        end

        scatter!(plt2, [px], [py], markersize=5, markercolor=:red)

        if !isempty(obstacles[i])
            obs_x = [o[1] for o in obstacles[i]]
            obs_y = [o[2] for o in obstacles[i]]
            obs_z = [o[3] for o in obstacles[i]]
            scatter!(plt1, obs_x, obs_y, obs_z, markersize=3, markercolor=:yellow, marker=:xcross)
            scatter!(plt2, obs_x, obs_y, markersize=3, markercolor=:yellow, marker=:xcross)
        end

        plot(plt1, plt2, layout = @layout([a{0.7w} b]), size=(900, 300))
    end every max(1, round(Int, 1/speed))

    gif(anim, fps=fps)
end

visualize_flight(landscape, drone_path, drone_heights, obstacles, speed, start, finish; fps=5)

[ Info: Saved animation to /user/start/examples/codegen/tmp.gif
Out[0]:
No description has been provided for this image

Conclusion

This code is a complete solution for simulating the flight of a drone over a random landscape. Let's list its main features.

  1. Flexibility of parameters: you can adjust the speed, altitude, viewing angle and obstacle detection range.
  2. Realistic visualization: 3D graphics and animation are used to visually represent the trajectory.
  3. Obstacle avoidance algorithm: the drone dynamically adjusts the route, avoiding collisions.

This code can serve as the basis for more complex simulations such as autonomous flights in an urban environment or terrain mapping. Further development may include integrating machine learning to optimize routes or processing data from real sensors.