Engee documentation
Notebook

Automated control systems

This example shows how to obtain frequency response data for a SISO model of a proportional-integral controller dynamic system.

The PI controller can make the error between the desired value and the actual value become zero. This means that it can achieve precision in regulation.

Its setup is quite simple. Only two parameters need to be configured: the gain factor (Kr) and the integration time constant (Ti). Using these parameters, it is possible to achieve a minimum adjustment error.

Reference materials for some libraries:

In [ ]: 
Pkg.add(["ControlSystems"])
In [ ]: 
# Установка новой библиотеки может занять около минуты
using ControlSystems

using Plots;
gr()
#plotlyjs() # для интерактивных графиков

print("Библиотеки готовы!")

Библиотеки готовы!

Connect SISO systems described in the state space

In [ ]: 
P1 = ssrand(1,1,1);
P2 = ssrand(1,1,1);
append(P1, P2)
Out[0]:
StateSpace{Continuous, Float64}
A = 
 -0.2524536214471187   0.0
  0.0                 -0.3574162051285983
B = 
 0.30175105771317484  0.0
 0.0                  1.1500354139870772
C = 
 0.6210941061472228  0.0
 0.0                 0.9581047028078271
D = 
 0.3742222874580735  0.0
 0.0                 0.1848146926902994

Continuous-time state-space model

Studying the response of the transfer function

Construct the LFCS of an open and closed system $$P(s) =\frac{1}{(s+1)^4}$$ using the function gangoffourplot() to draw conclusions about the sensitivity of the system to fluctuations at different frequencies.

In [ ]: 
P = ControlSystems.tf(1,[1,1])^4
gangoffourplot( P, tf(1), titlefont = font(9), guidefont = font(8))
Out[0]:

The graphs show that the system is too sensitive at frequencies around glad/s.

Setting up the PI controller

Set up the PI controller for the system $$P(s) = \frac{1}{(s+1)^4}$$

Use the function loopshapingPI, indicating that in the frequency range The rad/s system should have a 60 degree phase margin.

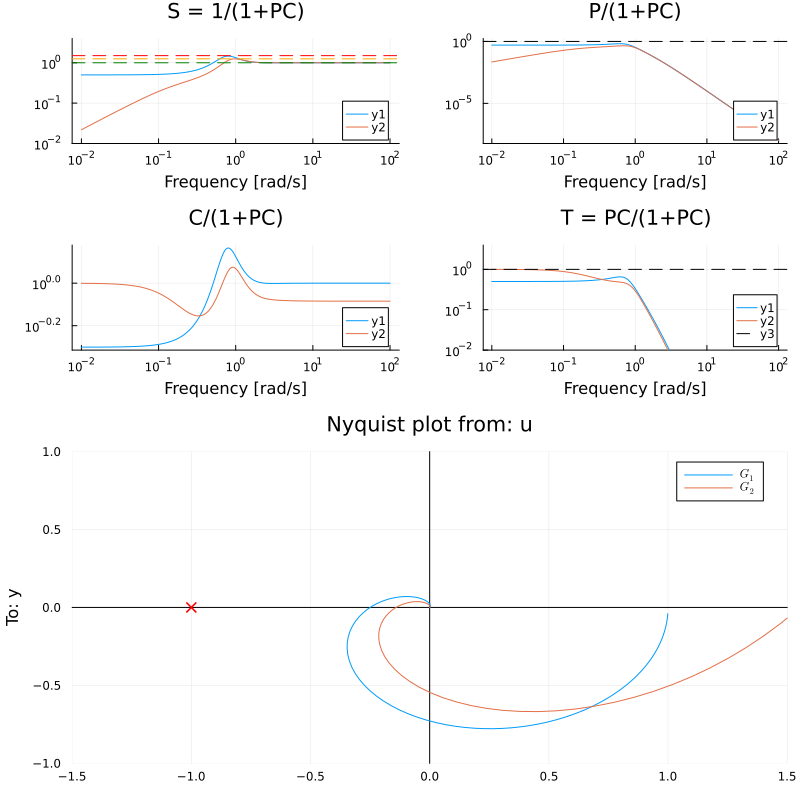
Output 4 graphs – LFCS for an open and for a closed system using the function gangoffourplot and the Nyquist hodograph using the function nyquistplot.

In [ ]: 
using ControlSystems, Plots

P = tf(1,[1,1])^4
ωp = 0.8
C,kp,ki = loopshapingPI(P, ωp, phasemargin=60, form=:parallel)

p1 = gangoffourplot(P, [tf(1), C]);
p2 = nyquistplot([P, P*C], ylims=(-1,1), xlims=(-1.5,1.5));

plot(p1,p2, layout=(2,1), size=(800,800))
Out[0]:

Conclusion

In the analyzed example, an analysis of the automated control system of the PI controller was carried out.

The response of the transfer function was also studied and the PI controller was adjusted.