Environment for manual adjustment of the PID controller
In this project, we suggest that you use a minimalistic environment to configure the PID controls for the graphical model of the system.
Description of the system
There is a model defined as a transfer function of the following type:
The task is to find the parameters of the PID controller at which the system satisfactorily performs a single step-by-step action.
Solution Steps
If this model is solved in the model editor, but does not demonstrate the parameters of the transition process that we are interested in, it's time to move on to the next stage and try to roughly select the parameters manually.
Since we obviously do not know the scale of the necessary parameters, in this example, each parameter of the PID controller is selected using two numbers.:
-
maximum value (unlimited),
-
Proportional coefficient (from 0 to 1)
This method provides some compromise between convenience and the breadth of the selected parameters. Without making modifications to the program code, the designer can set any scale of the regulator coefficients, and then smoothly select a more accurate value using a stepless regulator.
gr()
engee.open("pid_manual_tuning.engee")
using DataFrames, Statistics
all_runs = DataFrame[];
colors = [1, "skyblue", "lightblue", "powderblue", "lightblue1"];
The code of the next cell can be hidden by double-clicking on the form with controls. In addition, it is convenient to place the cell output to the right of the parameter input form (button ).
StopTime = 30 # @param {type:"slider",min:0,max:100,step:1}
P_max = 6.0 # @param {type:"number",placeholder:"1.0"}
I_max = 1.0 # @param {type:"number",placeholder:"1.0"}
D_max = 1.0 # @param {type:"number",placeholder:"1.0"}
P = 0.09 # @param {type:"slider",min:0,max:1,step:0.01}
I = 0.91 # @param {type:"slider",min:0,max:1,step:0.01}
D = 0 # @param {type:"slider",min:0,max:1,step:0.01}
engee.set_param!("pid_manual_tuning/PID controller", "P"=>P*P_max, "I"=>I*I_max, "D"=>D*D_max)
engee.set_param!("pid_manual_tuning", "StopTime"=>StopTime)
# Run the model and get the results.
data = engee.run("pid_manual_tuning")
x = collect(data["x"])
y = collect(data["y"])
# Delete the last item if the list is full.
pushfirst!(all_runs, y)
if length(all_runs) > 5 pop!(all_runs); end;
# Analysis of the last transition process
if length(all_runs) > 0
last_run = all_runs[1]
time_data = last_run.time
value_data = last_run.value
# We determine the steady-state value (the last 10% of the data)
steady_state_idx = Int.(collect((round(0.9 * length(value_data)):length(value_data))))
steady_state_value = mean(value_data[steady_state_idx])
# Defining the initial value
initial_value = value_data[1]
# Target value (we take it from the task)
target_value = x.value[end] # assuming that x is the assignment
# We find the maximum deviation (overshoot)
max_overshoot = maximum(value_data)
overshoot_percentage = abs((max_overshoot - steady_state_value) / (target_value - initial_value)) * 100
# Installation time (5%)
tolerance = 0.05 * abs(target_value - initial_value)
settling_time = nothing
for i in length(value_data):-1:1
if abs(value_data[i] - steady_state_value) > tolerance
settling_time = time_data[i]
break
end
end
# Rise time (10%-90%)
rise_time_10 = nothing
rise_time_90 = nothing
threshold_10 = initial_value + 0.1 * (steady_state_value - initial_value)
threshold_90 = initial_value + 0.9 * (steady_state_value - initial_value)
for i in 1:length(value_data)
if value_data[i] >= threshold_10 && rise_time_10 === nothing
rise_time_10 = time_data[i]
end
if value_data[i] >= threshold_90 && rise_time_90 === nothing
rise_time_90 = time_data[i]
break
end
end
rise_time = rise_time_90 - rise_time_10
# We display the results of the analysis
println("═"^50)
println("ANALYSIS OF THE TRANSITION PROCESS")
println("═"^50)
println("Steady-state value: $(round(steady_state_value, digits=3))")
println("Overshoot: $(round(overshoot_percentage, digits=1))%")
if settling_time !== nothing
println("Setup time (5%): $(round(setting_time, digits=2)) s")
else
println("Setup time: the process has not been established")
end
if rise_time !== nothing && rise_time_10 !== nothing
println("Rise time (10%-90%): $(round(rise_time, digits=2)) s")
end
# Static error (if any)
static_error = abs(target_value - steady_state_value)
if static_error > 1e-6
println("Static error: $(round(static_error, digits=4))")
else
println("Static error: missing")
end
# Number of fluctuations
peaks = 0
for i in 2:length(value_data)-1
if value_data[i] > value_data[i-1] && value_data[i] > value_data[i+1] &&
value_data[i] > steady_state_value
peaks += 1
end
end
println("Number of fluctuations: $peaks")
println("═"^50)
end
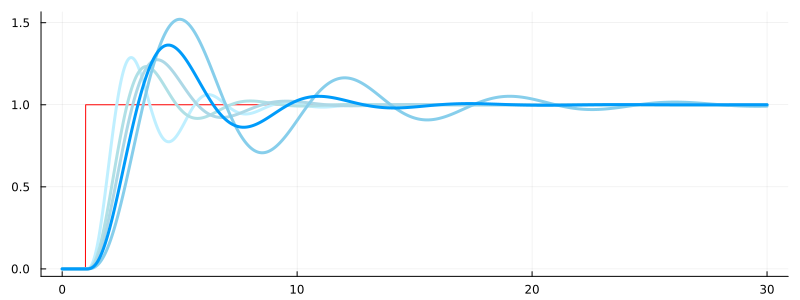
# Output the graphs
plot(x.time, x.value, c=:red, lw=1, size=(800,300), leg=false)
for i in length(all_runs):-1:1
plot!(all_runs[i].time, all_runs[i].value, c=colors[i], lw=3)
end
plot!()
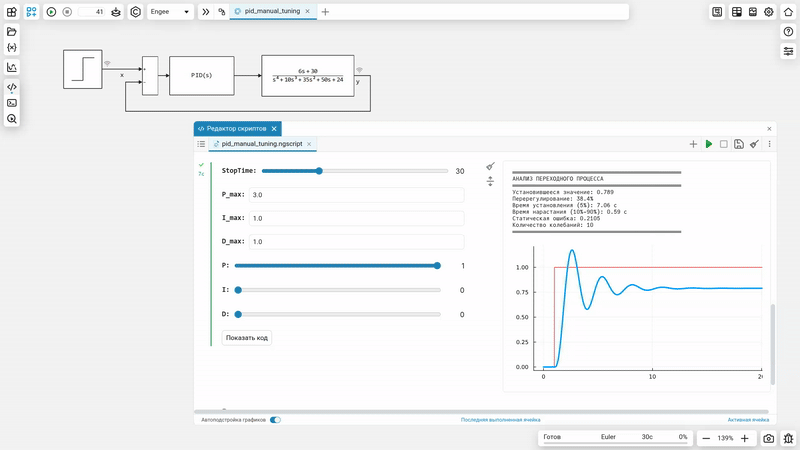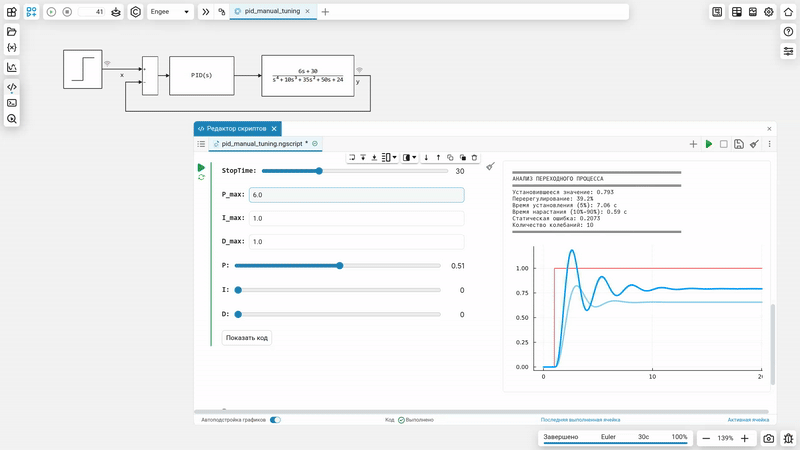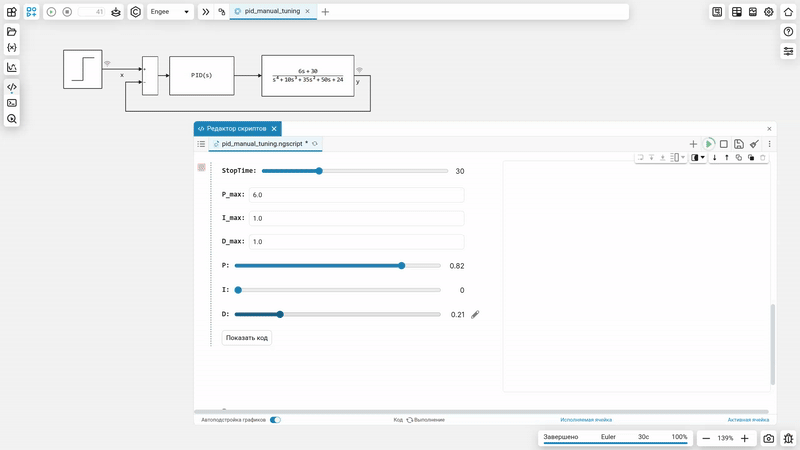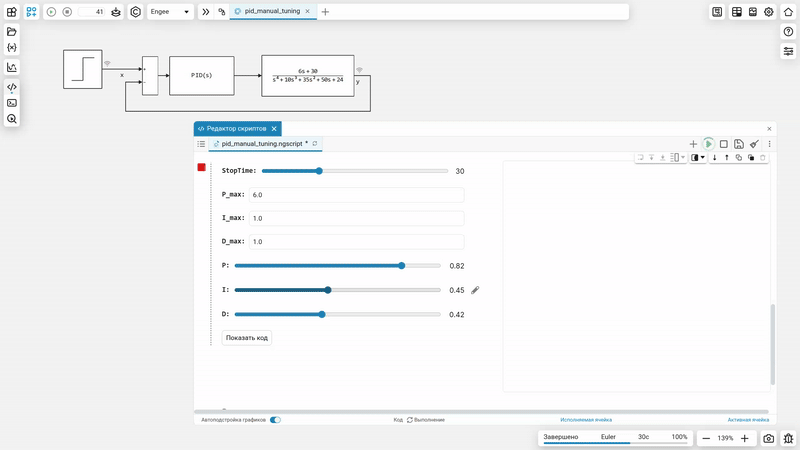
How it works
Conclusion
We have implemented a relatively rough method for manually selecting coefficients, which will allow you to adjust the parameters for a nonlinear, physical, linear or linearized system. The most cited method is the Ziegler-Nichols coefficient selection, and it could be implemented using the environment we created.