Engee documentation
Notebook

Short circuits on power lines in a network with a grounded neutral

Description of the model

This example considers a power system with a dead-earthed neutral consisting of two overhead lines with two-way power supply and one dead-end line at the end of which a short circuit (short circuit) occurs followed by disconnection (by default, the model has a single-phase short circuit to ground in phase A). The process of launching a model from the script development environment using command control, processing simulation results, calculating symmetric components, visualizing simulation results, and offering scenarios for independent work with the model are shown. The values of currents and voltages at three measurement points are logged, their time graphs and vector diagrams are shown, and the Fortescue transform is performed to calculate the symmetrical components. The model's appearance:

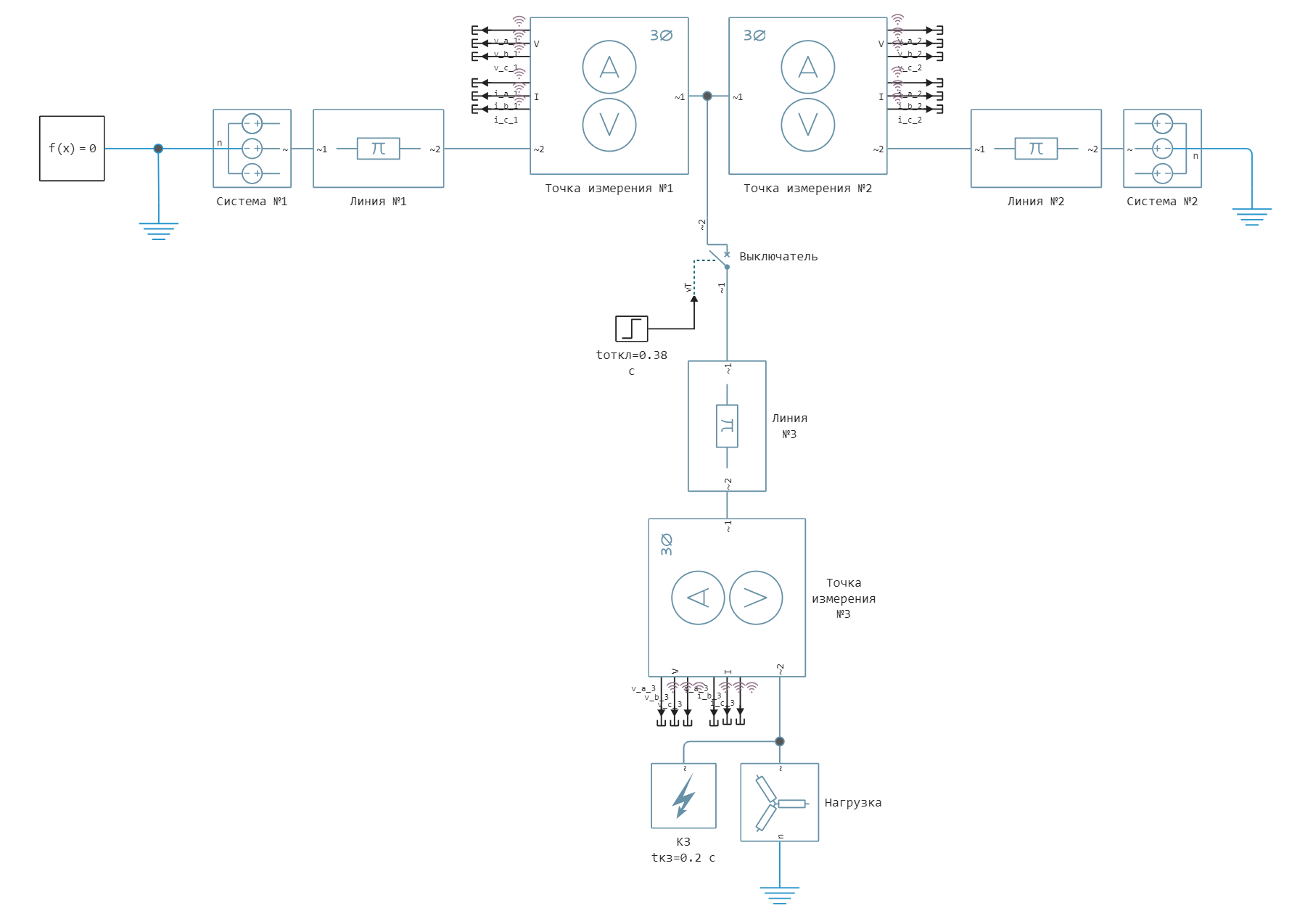
grounded_neutral_network_fault--1728649612571.png

The systems are modeled by [Voltage Source] blocks (Three-Phase)](https://engee.com/helpcenter/stable/ru/fmod-electricity-sources/voltage-source-three-phase.html) , the steady-state mode is set by setting the current line voltage and phase shift. Overhead lines are modeled by [Three-Phase PI Section] blocks Line](https://engee.com/helpcenter/stable/ru/fmod-electricity-lines/three-phase-pi-section-line.html). A short circuit is modeled by the [Fault] block (Three-Phase)](https://engee.com/helpcenter/stable/ru/fmod-electricity-utilities/fault-three-phase.html) in the settings of this block, using the Failure mode drop-down menu, you can select the type of short circuit. The short circuit is disabled using the [Circuit Breaker] block. (Three-Phase)](https://engee.com/helpcenter/stable/ru/fmod-electricity-switches-breakers/circuit-breaker-three-phase.html) , which simulates the operation of relay protection. The duration of the short-circuit shutdown is selected based on the operating time of the dead-end line protections with one-way power supply and the switch-off time, and is set to 0.18 s at the upper limit of the short-circuit shutdown duration for 110 kV in accordance with the Methodological Guidelines on the Stability of Power Systems from 2003 [1]. The load is modeled by the [Wye-Connected] block Load](https://engee.com/helpcenter/stable/ru/fmod-electricity-rlc-assemblies/wye-connected-load.html).
System parameters [2]:

Element Parameter
System No. 1 Balancing node
System No. 2

Load
Line No. 1 AC 185/29
Line No. 2 AC 185/29
Line No. 3 AC 150/24

Launching the model

We will import the necessary modules for working with graphs, tables, and a floating-window Fourier transform function.:

In [ ]: 
using Plots
using DataFrames
include("$(@__DIR__)/fourie_func.jl")
gr();

Loading the model:

In [ ]: 
model_name = "grounded_neutral_network_fault"
model_name in [m.name for m in engee.get_all_models()] ? engee.open(model_name) : engee.load( "$(@__DIR__)/$(model_name).engee");

Launching the uploaded model:

In [ ]: 
results = engee.run(model_name);

Simulation results

To import the simulation results, logging of the necessary signals was enabled in advance and their names were set. Converting the instantaneous values of currents and voltages of the results variable into separate vectors:

In [ ]: 
# вектор времени симуляции
sim_time = results["i_a_1"].time;
# вектор токов в точке измерения №1
i_1 = hcat(results["i_a_1"].value,results["i_b_1"].value,results["i_c_1"].value);
# вектор токов в точке измерения №2
i_2 = hcat(results["i_a_2"].value,results["i_b_2"].value,results["i_c_2"].value);
# вектор токов в точке измерения №3
i_3 = hcat(results["i_a_3"].value,results["i_b_3"].value,results["i_c_3"].value);
# вектор напряжений в точке измерения №1
v_1 = hcat(results["v_a_1"].value,results["v_b_1"].value,results["v_c_1"].value);
# вектор напряжений в точке измерения №2
v_2 = hcat(results["v_a_2"].value,results["v_b_2"].value,results["v_c_2"].value);
# вектор напряжений в точке измерения №3
v_3 = hcat(results["v_a_3"].value,results["v_b_3"].value,results["v_c_3"].value);

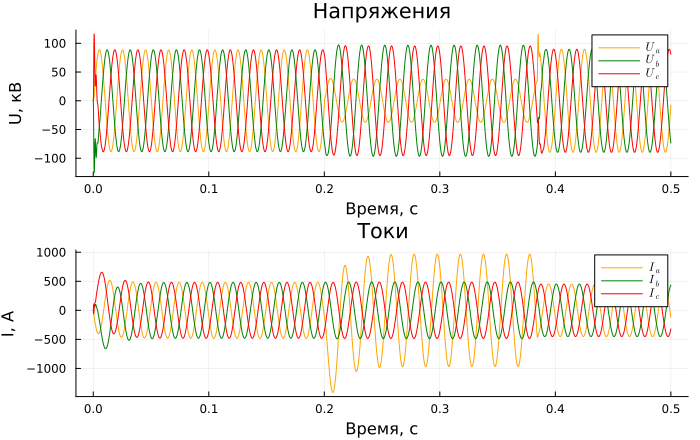
Graphs of currents and voltages at the measuring point No. 1:

In [ ]: 
p1 = Plots.plot(sim_time, v_1./1e3, label = [L"U_a" L"U_b" L"U_c"],
title = "Напряжения", ylabel = "U, кВ", xlabel="Время, c");
p2 = Plots.plot(sim_time, i_1, label = [L"I_a" L"I_b" L"I_c"],
title = "Токи", ylabel = "I, А", xlabel="Время, c")
plot(p1, p2, layout=(2,1), legend = true, linecolor = [:orange :green :red], size = (700,440))
Out[0]:

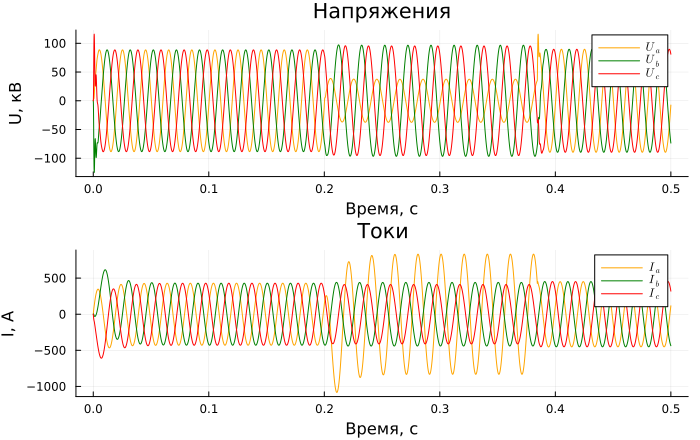
Graphs of currents and voltages at the measuring point No. 2:

In [ ]: 
p1 = Plots.plot(sim_time, v_2./1e3, label = [L"U_a" L"U_b" L"U_c"],
title = "Напряжения", ylabel = "U, кВ", xlabel="Время, c");
p2 = Plots.plot(sim_time, i_2, label = [L"I_a" L"I_b" L"I_c"],
title = "Токи", ylabel = "I, А", xlabel="Время, c")
plot(p1, p2, layout=(2,1), legend = true, linecolor = [:orange :green :red], size = (700,440))
Out[0]:

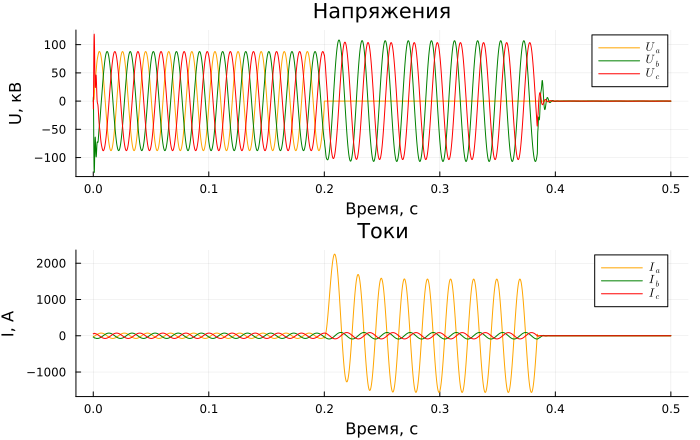
Graphs of currents and voltages at the measuring point No. 3

In [ ]: 
p1 = Plots.plot(sim_time, v_3./1e3, label = [L"U_a" L"U_b" L"U_c"],
title = "Напряжения", ylabel = "U, кВ", xlabel="Время, c");
p2 = Plots.plot(sim_time, i_3, label = [L"I_a" L"I_b" L"I_c"],
title = "Токи", ylabel = "I, А", xlabel="Время, c")
plot(p1, p2, layout=(2,1),legend = true, linecolor = [:orange :green :red], size = (700,440))
Out[0]:

As a result of a single-phase short circuit, the voltage of the damaged phase decreases and the current increases. Note that the voltage of the damaged phase increases as you move away from the damage site.

Processing of results

Let's evaluate the effect of short-circuit on the asymmetry of currents. Calculation of symmetric components using the Fortescue transform [3]:

To do this, we perform vectorization of the currents using a Fourier transform with a floating window to isolate the amplitudes and phases.
At the same time, we will not use the built-in functions and will use the function [4]:

In [ ]: 
# Переменные для хранения векторов
v_1_Xmag, v_2_Xmag, v_3_Xmag, i_1_Xmag, i_2_Xmag, i_3_Xmag,
v_1_Xphase, v_2_Xphase, v_3_Xphase, i_1_Xphase, i_2_Xphase, i_3_Xphase = [zeros(length(sim_time),3) for _ = 1:12];

for (Xmag, Xphase, signal) in zip(
    (v_1_Xmag, v_2_Xmag, v_3_Xmag, i_1_Xmag, i_2_Xmag, i_3_Xmag),
    (v_1_Xphase, v_2_Xphase, v_3_Xphase, i_1_Xphase, i_2_Xphase, i_3_Xphase),
    (v_1, v_2, v_3, i_1, i_2, i_3))
    Xmag, Xphase = moving_fourie(Xmag, Xphase, sim_time, signal);
end

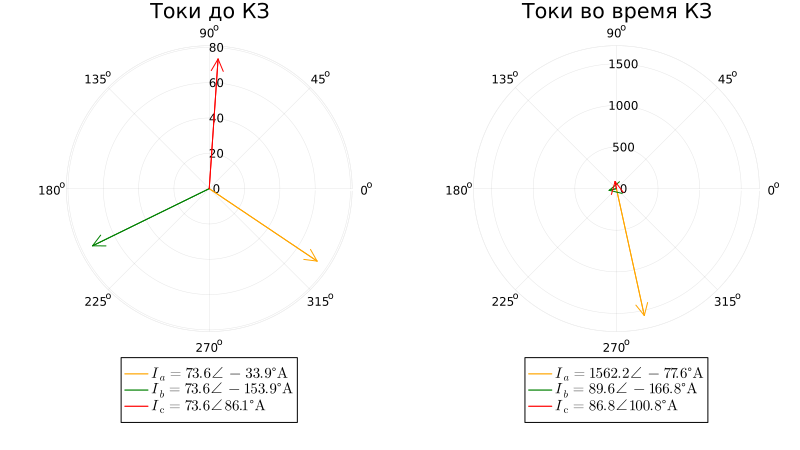
Vector diagram of currents at measuring point No. 3 before and during short circuit:

In [ ]: 
# поиск индексов моментов до и после КЗ (0.1 с и 0.3 с)
nom_reg_ind = indexin(0.1, sim_time);
kz_ind = indexin(0.3, sim_time);
# ампитуды и фазы токов
i_a_NR_mag, i_a_NR_ang = round(i_3_Xmag[nom_reg_ind,1][1], digits=1), round(i_3_Xphase[nom_reg_ind,1][1], digits=1)
i_b_NR_mag, i_b_NR_ang = round(i_3_Xmag[nom_reg_ind,2][1], digits=1), round(i_3_Xphase[nom_reg_ind,2][1], digits=1)
i_c_NR_mag, i_c_NR_ang = round(i_3_Xmag[nom_reg_ind,3][1], digits=1), round(i_3_Xphase[nom_reg_ind,3][1], digits=1)
i_a_SC_mag, i_a_SC_ang = round(i_3_Xmag[kz_ind,1][1], digits=1), round(i_3_Xphase[kz_ind,1][1], digits=1)
i_b_SC_mag, i_b_SC_ang = round(i_3_Xmag[kz_ind,2][1], digits=1), round(i_3_Xphase[kz_ind,2][1], digits=1)
i_c_SC_mag, i_c_SC_ang = round(i_3_Xmag[kz_ind,3][1], digits=1), round(i_3_Xphase[kz_ind,3][1], digits=1)

p1 = plot([0;i_a_NR_ang*pi/180], [0;i_a_NR_mag], arrow=true, proj = :polar, linecolor = :orange, 
label = L"I_a = %$i_a_NR_mag \angle\, %$i_a_NR_ang \degree А", title = "Токи до КЗ")

plot!([0;i_b_NR_ang*pi/180], [0;i_b_NR_mag], arrow=true, proj = :polar, linecolor = :green,
label = L"I_b = %$i_b_NR_mag \angle\, %$i_b_NR_ang \degree А")

plot!([0;i_c_NR_ang*pi/180], [0;i_c_NR_mag], arrow=true, proj = :polar, linecolor = :red,
label = L"I_с = %$i_c_NR_mag \angle\, %$i_c_NR_ang \degree А")

p2 = plot([0;i_a_SC_ang*pi/180], [0;i_a_SC_mag], arrow=true, proj = :polar, linecolor = :orange,
label = L"I_a = %$i_a_SC_mag \angle\, %$i_a_SC_ang \degree А", title = "Токи во время КЗ")

plot!([0;i_b_SC_ang*pi/180], [0;i_b_SC_mag], arrow=true, proj = :polar, linecolor = :green,
label = L"I_b = %$i_b_SC_mag \angle\, %$i_b_SC_ang \degree А")

plot!([0;i_c_SC_ang*pi/180], [0;i_c_SC_mag], arrow=true, proj = :polar, linecolor = :red,
label = L"I_с = %$i_c_SC_mag \angle\, %$i_c_SC_ang \degree А")

plot(p1, p2, layout=(1,2), legend = :outerbottom, legendfontsize=10, size = (800,450))
Out[0]:

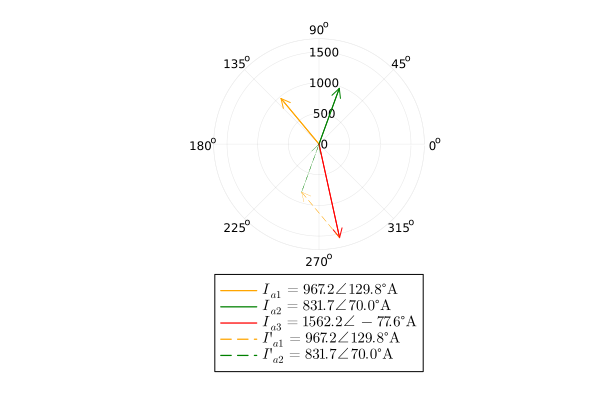
Consider the current distribution of phase A at the junction of line No. 1-3 during a short circuit in the vector diagram:

In [ ]: 
# вектора токов в комплексных числах
i_a_1_mag, i_a_1_ang = round(i_1_Xmag[kz_ind,1][1], digits=1), round(i_1_Xphase[kz_ind,1][1], digits=1)
i_a_2_mag, i_a_2_ang = round(i_2_Xmag[kz_ind,1][1], digits=1), round(i_2_Xphase[kz_ind,1][1], digits=1)
i_a_3_mag, i_a_3_ang = round(i_3_Xmag[kz_ind,1][1], digits=1), round(i_3_Xphase[kz_ind,1][1], digits=1)
ia1 = i_a_1_mag*exp(1im*i_a_1_ang*pi/180)
ia2 = i_a_2_mag*exp(1im*i_a_2_ang*pi/180)
ia3 = i_a_3_mag*exp(1im*i_a_3_ang*pi/180)

plot([0;angle(ia1)], [0;abs(ia1)],
 arrow=true, proj = :polar, linecolor = :orange, label =  L"I_{a1} = %$i_a_1_mag \angle\, %$i_a_1_ang \degree А")

plot!([0;angle(ia2)], [0;abs(ia1)],
 arrow=true, proj = :polar, linecolor = :green, label = L"I_{a2} = %$i_a_2_mag \angle\, %$i_a_2_ang \degree А")

plot!([0;angle(ia3)], [0;abs(ia3)],
 arrow=true, proj = :polar, linecolor = :red, label = L"I_{a3} = %$i_a_3_mag \angle\, %$i_a_3_ang \degree А")

# вспомогательный вектор Ia3+Ia1
plot!([angle(ia3);angle(ia3+ia1)], [abs(ia3);abs(ia3+ia1)],
 arrow=true, proj = :polar, linecolor = :orange, label = L"I'_{a1} = %$i_a_1_mag \angle\, %$i_a_1_ang \degree А",
  ls = :dash, linewidth=0.3)

# вспомогательный вектор Ia3+Ia1+Ia2
plot!([angle(ia3+ia1);angle(ia3+ia1+ia2)], [abs(ia3+ia1);abs(ia3+ia1+ia2)], arrow=true, proj = :polar, linecolor = :green,
label = L"I'_{a2} = %$i_a_2_mag \angle\, %$i_a_2_ang \degree А", ls = :dash, linewidth=0.3, legendfontsize=10, legend = :outerbottom)
Out[0]:

The vector diagram shows that the geometric sum of the currents is and is equal to the current , and all the currents add up to 0. This diagram shows the fulfillment of Kirchhoff's first law for a node.

Calculate the symmetrical components of the currents:

In [ ]: 
a = exp(2pi*1im/3)
a_matr = [1 1 1;
         a a^2 1;
         a^2 a 1;]
# симметричные составляющие: [I1 I2 I0]
i_3_sym = 1/3*(i_3_Xmag .* exp.(1im .* i_3_Xphase .* (pi/180)))*a_matr;

Let's tabulate the values of the amplitudes and symmetrical components of the currents (measuring point No. 3) before and during the short circuit.:

In [ ]: 
# Токи №3
println("\n"*"Токи в точке измерения №3")
println(DataFrame([["Ном.реж.", "КЗ"], 
round.([i_3_Xmag[nom_reg_ind,1][1]; i_3_Xmag[kz_ind,1][1]],digits = 1),
round.([i_3_Xmag[nom_reg_ind,2][1]; i_3_Xmag[kz_ind,2][1]],digits = 1),
round.([i_3_Xmag[nom_reg_ind,3][1]; i_3_Xmag[kz_ind,3][1]],digits = 1),
round.(abs.([i_3_sym[nom_reg_ind,1][1]; i_3_sym[kz_ind,1][1]]),digits = 1),
round.(abs.([i_3_sym[nom_reg_ind,2][1]; i_3_sym[kz_ind,2][1]]),digits = 1),
round.(abs.([i_3_sym[nom_reg_ind,3][1]; i_3_sym[kz_ind,3][1]]),digits = 1)], 
["Режимы", "I_a (А)", "I_b (А)", "I_c (А)", "I_1 (А)", "I_2 (А)", "I_0 (А)"]))

Токи в точке измерения №3
2×7 DataFrame
 Row │ Режимы    I_a (А)  I_b (А)  I_c (А)  I_1 (А)  I_2 (А)  I_0 (А) 
     │ String    Float64  Float64  Float64  Float64  Float64  Float64 
─────┼────────────────────────────────────────────────────────────────
   1 │ Ном.реж.     73.6     73.6     73.6     73.6      0.0      0.0
   2 │ КЗ         1562.2     89.6     86.8    563.0    508.5    493.1

With a single-phase short circuit to earth, the components of the reverse and zero sequences appear, and they are practically equal to each other. The slight difference in values is due to the presence of a load at the end of line No. 3.

Addition

Try to change the following model parameters yourself and investigate how this affects the operating mode of the power system:

  1. the length of line No. 3 is 60 km;
  2. Type of fault in the Fault (Three-Phase) block;
  3. The value of the short-circuit transition resistance at 0.1 ohms in the Fault (Three-Phase) block;
  4. 3-phase short circuit power for 3000 MVA power supplies - Voltage Source (Three-Phase) units.

Conclusions

In this example, tools were used for command management of the Engee model and uploading simulation results, and work with the Plots and DataFrames modules is shown. The measured currents and voltages were imported into the Workspace from the result variable and then displayed on time graphs. They were then vectorized using a Fourier transform with a floating window and shown on vector diagrams. Based on the obtained vectors of currents and voltages using the Fortescue transform, the symmetric components are calculated and tabulated.

Links

  1. Methodological guidelines on the stability of energy systems.
    Approved by the Order of the Ministry of Energy of Russia dated June 30, 2003 N 277.
  2. Handbook on the design of electrical networks /
    edited by D. L. Faybisovich. – 4th ed., revised and add. – M. : ENAS, 2012. – 376 p. : ill.
  3. Zeveke G.V., Ionkin P.A., Netushil A.V., Strakhov S.V. Fundamentals of circuit theory (4th ed., 1975).
  4. Microprocessor relays : a textbook / A. A. Nikitin ; Ministry of Education and Science of the Russian Federation, Federal Agency for Education, Federal State Educational Institution higher Prof. education "Chuvash State University named after I. N. Ulyanov". Cheboksary : Publishing House of the Chuvash University, 2006. 447 p.; ISBN 5-7677-1051-1

Blocks used in example