The algorithm for constructing a convex hull

We are considering the implementation of an algorithm for constructing a convex hull (convex hull) of a set of points in a two-dimensional space in the Julia language.

Introduction

The convex hull construction algorithm is a geometric algorithm that finds the minimum convex polygon containing all the specified points. Simply put, imagine that you have a set of nails on a board, and you pull an elastic band around them — the shape of this elastic band will be a convex hull.

This algorithm is used in many fields: computer graphics, pattern recognition, optimization, robotics, and others. In this example, we use the library Polyhedra.jl to work with polyhedra, namely with the V-representation of points (Vertex representation), to build a convex hull of points.

The main part

Installing the necessary packages (if not already installed)

import Pkg; Pkg.add(["Polyhedra", "CDDLib"])

Connecting libraries

Polyhedra — the main library for working with polyhedra

CDDLib — library for calculations with polyhedra using the double description method

using Polyhedra, CDDLib, Makie

Defining a set of points as a vertex representation (V-representation).

Each point is the coordinates [x, y]

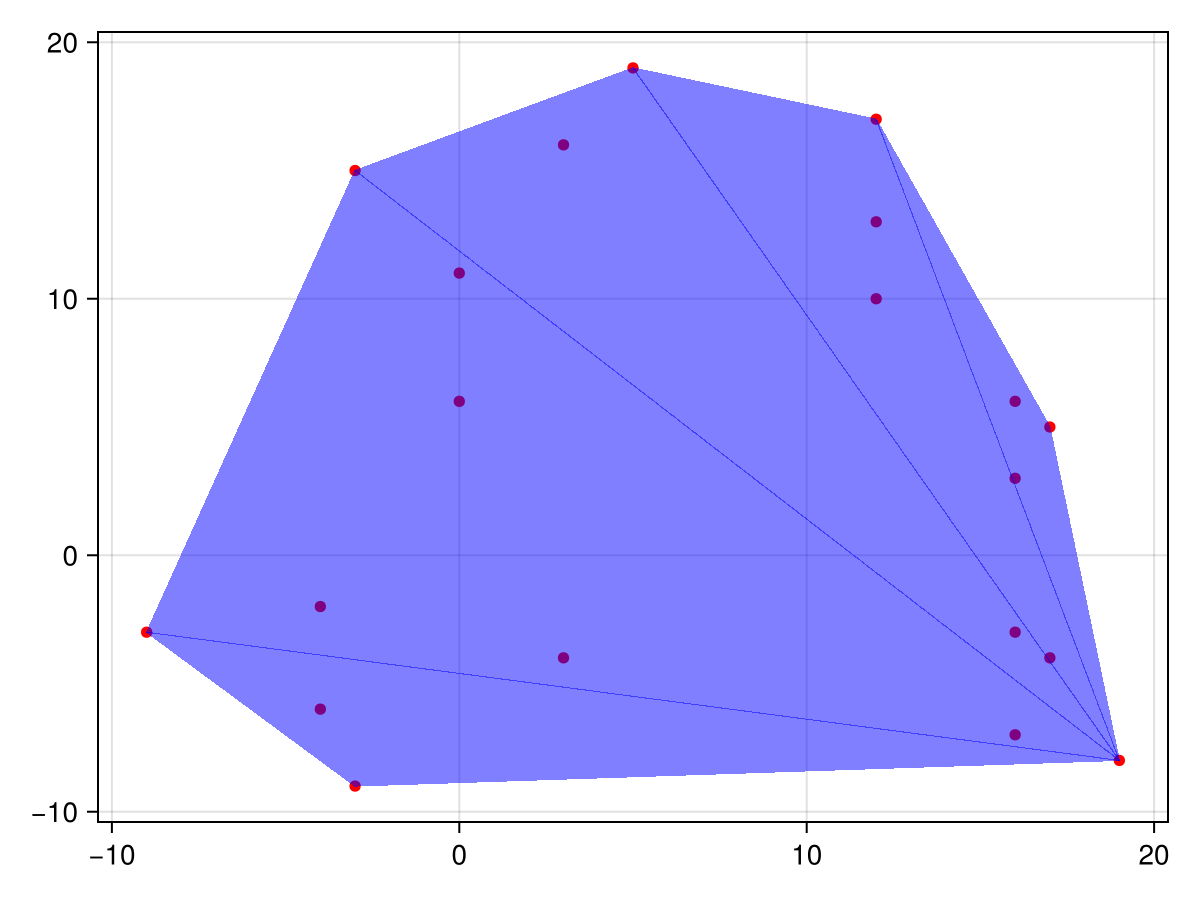
Dots = [
    [16,3],  [12,17], [0,6],  [-4,-6], [16,6],
    [16,-7], [16,-3], [17,-4], [5,19], [19,-8],
    [3,16],  [12,13], [3,-4], [17,5],  [-3,15],
    [-3,-9], [0,11],  [-9,-3], [-4,-2], [12,10]
];

vrep — this is a function that creates an object. Vertex Representation from the list of points

A = vrep(Dots)

V-representation Polyhedra.PointsHull{Int64, Vector{Int64}, Int64}:
20-element iterator of Vector{Int64}:
 [16, 3]
 [12, 17]
 [0, 6]
 [-4, -6]
 [16, 6]
 [16, -7]
 [16, -3]
 [17, -4]
 [5, 19]
 [19, -8]
 [3, 16]
 [12, 13]
 [3, -4]
 [17, 5]
 [-3, 15]
 [-3, -9]
 [0, 11]
 [-9, -3]
 [-4, -2]
 [12, 10]

Creating a polyhedron object from a V-representation

The backend is being used CDDLib to perform all calculations

P = polyhedron(A, CDDLib.Library())

Polyhedron CDDLib.Polyhedron{Float64}:
20-element iterator of Vector{Float64}:
 [16.0, 3.0]
 [12.0, 17.0]
 [0.0, 6.0]
 [-4.0, -6.0]
 [16.0, 6.0]
 [16.0, -7.0]
 [16.0, -3.0]
 [17.0, -4.0]
 [5.0, 19.0]
 [19.0, -8.0]
 [3.0, 16.0]
 [12.0, 13.0]
 [3.0, -4.0]
 [17.0, 5.0]
 [-3.0, 15.0]
 [-3.0, -9.0]
 [0.0, 11.0]
 [-9.0, -3.0]
 [-4.0, -2.0]
 [12.0, 10.0]

Let's construct points and a convex polyhedron:

# Creating a mesh from a polyhedron P
m = Polyhedra.Mesh(P);

# Extracting the X and Y coordinates from the Dots vector
X = [dot[1] for dot in Dots]  # The first elements are the X coordinates
Y = [dot[2] for dot in Dots]  # The second elements are the Y coordinates

# Creating a shape and axes for the graph
fig = Figure()
ax = Axis(fig[1, 1])

# Drawing points on the graph
Makie.scatter!(ax, X, Y, markersize=8, color=:red)

# Draw the polyhedron grid in translucent blue
Makie.mesh!(m, color=(:blue,0.5))

# Displaying a shape
fig

Construction of the convex hull of a polyhedron P with myself (in fact, we get the same convex hull)

This operation creates a new object representing the convex hull of two polyhedra.

Pch = convexhull(P, P)

Polyhedron CDDLib.Polyhedron{Float64}:
40-element iterator of Vector{Float64}:
 [16.0, 3.0]
 [12.0, 17.0]
 [0.0, 6.0]
 [-4.0, -6.0]
 [16.0, 6.0]
 [16.0, -7.0]
 [16.0, -3.0]
 [17.0, -4.0]
 [5.0, 19.0]
 [19.0, -8.0]
 [3.0, 16.0]
 [12.0, 13.0]
 [3.0, -4.0]
 [17.0, 5.0]
 [-3.0, 15.0]
 [-3.0, -9.0]
 [0.0, 11.0]
 [-9.0, -3.0]
 [-4.0, -2.0]
 [12.0, 10.0]
 [16.0, 3.0]
 [12.0, 17.0]
 [0.0, 6.0]
 [-4.0, -6.0]
 [16.0, 6.0]
 [16.0, -7.0]
  ⋮

Removing redundant points/vertices from the view

That is, only the vertices that are really needed to describe the boundaries of the convex polygon remain.

removevredundancy!(Pch)

Displaying the result on the screen - information about the polyhedron (vertices, edges, etc.)

println("$Pch")

convexhull([5.0, 19.0], [19.0, -8.0], [17.0, 5.0], [-3.0, 15.0], [-9.0, -3.0], [12.0, 17.0], [-3.0, -9.0])

What happens step by step?

We define a set of points in the plane.
Using these points, we form a V-representation, which is a way of describing a shape through its vertices.
Create an object of the "polyhedron" type, which is stored in the library's internal format. Polyhedra.
We build a convex hull (in this case, we actually copy it, since we combine the polyhedron with itself).
Remove excess points from the resulting object, leaving only those that actually define the boundaries of the shape.
We print the result: information about the vertices of the convex polygon will be displayed.

Conclusion

We have reviewed a simple example of using the library. Polyhedra.jl Julia programming language for constructing a convex hull set of points. Thanks to the powerful capabilities of this library and the support of various backends, polyhedral structures can be easily built, analyzed, and visualized. This can be useful when solving problems from linear programming, computer graphics, and analytical geometry.

To summarize, this example allows a beginner to understand the principles of working with geometric data and polyhedra in Julia.

The example was developed using materials from Rosetta Code