Engee documentation
Notebook

Filtering of noisy signal by sliding averaging

This example shows how to perform moving average (simple and exponential) filtering using the Moving RMS block. By changing the block settings we will get four different filter behaviours.

Description of the model and filters

Block Pulse Generator generates rectangular pulses of 512 time samples each. Block Switch controls the switching between upper and lower meander levels (between 0.5 and 1.5). We add to this signal noise with mathematical expectation 0 and variance 0.001.

For smoothing by the sliding window method (moving average (MA)) or FIR filter, we implement two modes differing in the window overlap ratio. In one case the filter will make a jump for 1 measurement, in the other for 4 measurements. The result of these filters will be almost the same in terms of the output value, but the discretisation of the filter with overlap of 4 will be 4 times lower than that of the filter with a jump of 1.

We also implement a set of BIR filters with exponential smoothing (exponential moving average (EMA)), for which we set different weight coefficients: 0.9 and 0.99. They significantly affect the output signal: the graph with a smaller value of the smoothing coefficient (0.9) will react more dynamically both to the noise and to the signal switching between levels.

More details about the operation of these smoothing methods and their parameters can be found in the [Moving RMS] block help (https://engee.com/helpcenter/stable/dsp-statistics/moving-rms.html).

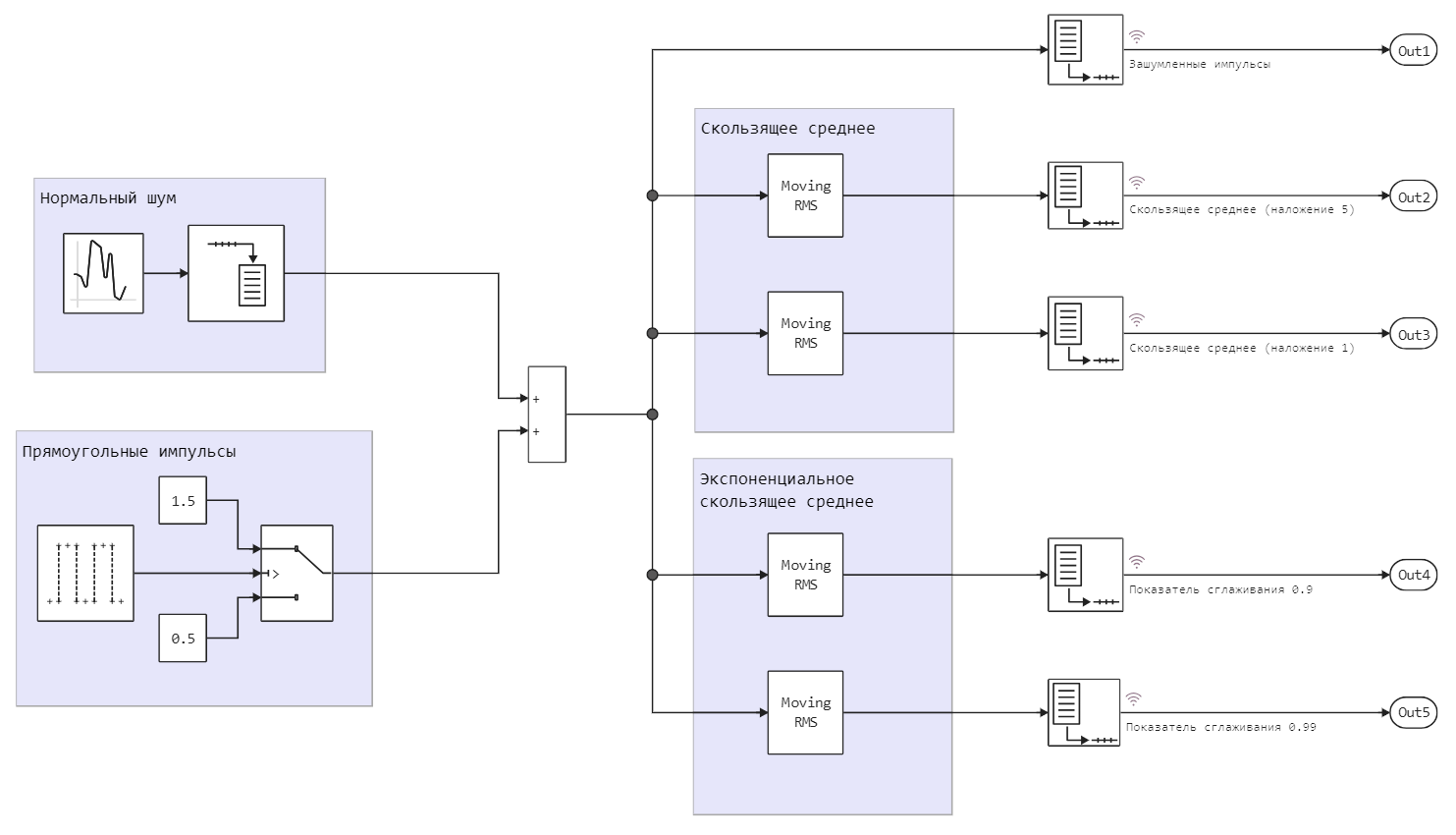
image.png

Individual areas of the model are highlighted using annotations that encapsulate the SVG markup.

Sampling rate of the model

Since in Engee it is necessary to specify the step size of the model, working with multirate models requires careful attention to the discretisation of different blocks. Let's look at one situation. A noise generator is triggered 512 times more often than a pulse generator. The model is configured to produce 44100 measurements per second.

If the first smoothing filter has a smoothing window jump size of 4, then the sampling rate of the signal after this filter will be equal to (512/4)/44100, i.e. 128/44100 (we can say 128 samples).

But if we want to make the jump size equal to 5, we will have to change the base sampling rate of the model. Indeed, at the output of such a filter, the signal will be sampled at (512/5)/44100, i.e. 102.4/44100 (fractional number of samples). In such a case, the base sampling rate of the model is no longer a common divisor for the sampling rate of all signals on the canvas. It will need to be increased by a factor of 5 (5*44100) to restore the model's performance.

Running the model

Let's run the model by means of programme control and compare the results of different filters.

In [ ]: 
modelName = "mvgRMSNoisyStep";
model = modelName in [m.name for m in engee.get_all_models()] ? engee.open( modelName ) : engee.load( "$(@__DIR__)/$(modelName).engee");
engee.set_param!( modelName, "StopTime"=>8 );
data = engee.run( modelName, verbose=false )
Out[0]:
Dict{String, DataFrame} with 5 entries:
  "MA - Размер скачка 4"              => 88201×2 DataFrame…
  "MA - Размер скачка 1"              => 352801×2 DataFrame…
  "EMA - Показатель сглаживания 0.9"  => 352801×2 DataFrame…
  "EMA - Показатель сглаживания 0.99" => 352801×2 DataFrame…
  "Зашумленные импульсы"              => 352801×2 DataFrame…

Draw a general graph:

In [ ]: 
plot( data["Зашумленные импульсы"].time[1:4:end], data["Зашумленные импульсы"].value[1:4:end],
    c=5, label="Зашумленные импульсы" )
plot!( data["MA - Размер скачка 4"].time[1:4:end], data["MA - Размер скачка 4"].value[1:4:end],
    c=1, label="Размер скачка 4" )
plot!( data["MA - Размер скачка 1"].time[1:4:end], data["MA - Размер скачка 1"].value[1:4:end],
    c=2, label="Размер скачка 1" )
plot!( data["EMA - Показатель сглаживания 0.9"].time[1:4:end], data["EMA - Показатель сглаживания 0.9"].value[1:4:end],
    c=3, label="Показатель сглаживания 0.9" )
plot!( data["EMA - Показатель сглаживания 0.99"].time[1:4:end], data["EMA - Показатель сглаживания 0.99"].value[1:4:end],
    c=4, label="Показатель сглаживания 0.99" )
Out[0]:

Let's zoom in on the graph to see how different smoothing algorithms handle a sudden change in signal level.

In [ ]: 
r1 = 65500:65800
r2 = 4 .* r1

plot( data["Зашумленные импульсы"].time[r2], data["Зашумленные импульсы"].value[r2],
       c=5, label="Зашумленные импульсы" )
plot!( data["MA - Размер скачка 4"].time[r1], data["MA - Размер скачка 4"].value[r1],
        c=1, label="Размер скачка 4" )
plot!( data["MA - Размер скачка 1"].time[r2], data["MA - Размер скачка 1"].value[r2],
        c=2, label="Размер скачка 1" )
plot!( data["EMA - Показатель сглаживания 0.9"].time[r2], data["EMA - Показатель сглаживания 0.9"].value[r2],
        c=3, label="Показатель сглаживания 0.9" )
plot!( data["EMA - Показатель сглаживания 0.99"].time[r2], data["EMA - Показатель сглаживания 0.99"].value[r2],
        c=4, label="Показатель сглаживания 0.99" )
Out[0]:

Conclusion

We have compared several methods of signal averaging performed with the help of Moving RMS block with different settings and we can implement the algorithm we need and objectively choose the best way of filtering.

Blocks used in example