Multi-speed filter

Introduction

Multi-rate systems are called discrete systems containing signals with different sampling rates (BH). In most cases, systems that change the sampling frequency of the input signal are considered. It can be increased and decreased by an integer number of times, as well as changed by a fractional number of times (m/n, where m and n - whole ones). Using the example of this model, we will consider the classic problem of changing the BH by a fractional number of times, and also find out why we need a filter.

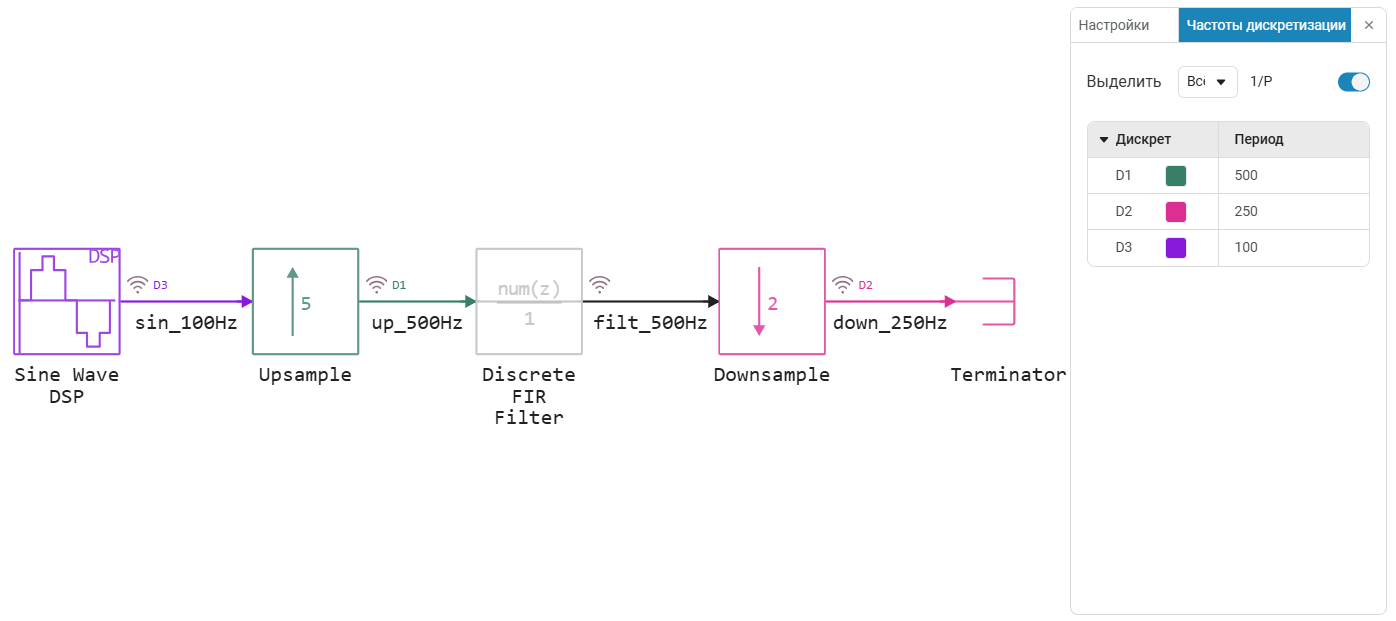
The model consists of blocks of a discrete sinusoidal signal source DSP Sine Wave, the block of increasing the BH by an integer number of times Upsample, the block of lowering the BH by an integer number of times Downsample, and the filter block Discrete FIR Filter, which is initially inactive (the signal passes through the block unchanged). The original discrete sine wave is a signal with a fundamental frequency of 5 Hz and a sampling frequency of 100 Hz.
Block Upsample increases the BH by 5 times in a very simple way - by adding four additional zeros between the counts of the incoming sine wave.
Block Downsample it cuts through the samples of the incoming signal, removing (in our case) every second.
Thus, we want to increase the BH of the sine wave by 2.5 times.
On the tab Отладка in the model, we highlight the BH of the blocks and signals in different colors.

Model launch and output waveform

When running the model for simulation, we can observe in the window Графики time domain signals.
Note that the original signal looks like a discrete (stepwise) sinusoid, while the
output of the model (a 250 Hz BH signal) is an outlier with zeros between them.

Blocks Upsample and Downsample - implement simple digital algorithms that change the BH.
But they do not perform interpolation and decimation in the usual sense.

To understand how the block helps with such operations.
Discrete FIR Filter Let's first look at what happens
to the signal spectrum when the BH increases and decreases.

Spectral copying and aliasing when changing the sampling rate

To do this, use the built-in interactive tools to
visualize the signal spectrum in the window Графики by selecting
in Меню сигналов: Сигналы в частотной области. We will
display the signals sequentially (it is important to understand that for correct display
on the same axes, the signals must have the same sampling frequency).

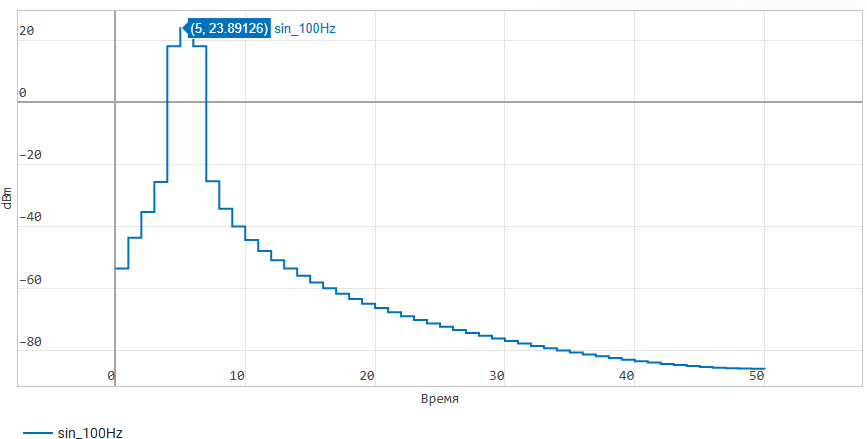
First, we will display the spectrum of the original discrete sinusoid. Let's make sure
that the peak of the spectrum is at a frequency of 5 Hz, and the X-axis of the graph
lies in the range from 0 to 50 Hz (i.e. up to half the sampling frequency):

Now let's consider the signal spectrum after increasing the BH by a factor of 5.:

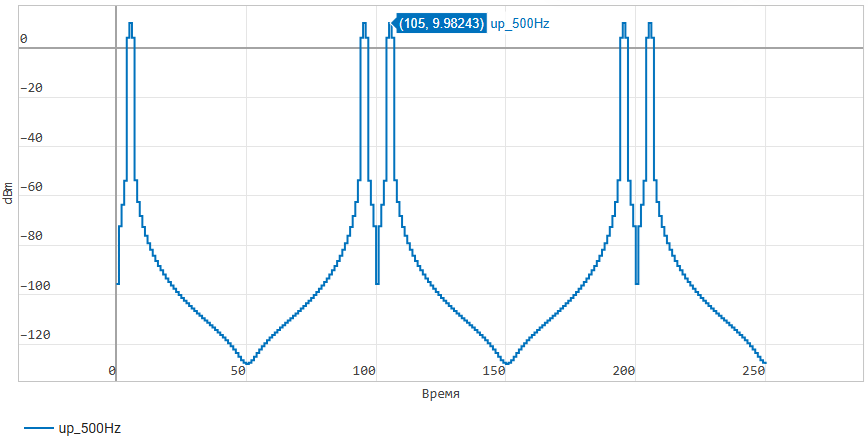
The spectrum of a discrete signal is inherently periodic,
and when the frequency observation zone (Nyquist zone) is expanded
to a new value of half the BH, we begin to observe
spectral copies of our signal.
In our case, the sinusoids are visible at frequencies of 5 Hz, 95 Hz,
105 Hz, 195 Hz, 205 Hz.

And with a further narrowing of the observation area of the spectrum after surgery
Downsample these copies
are "wrapped" in a new Nyquist zone, which is now restricted.
the value is 125 Hz. This is the aliasing effect:

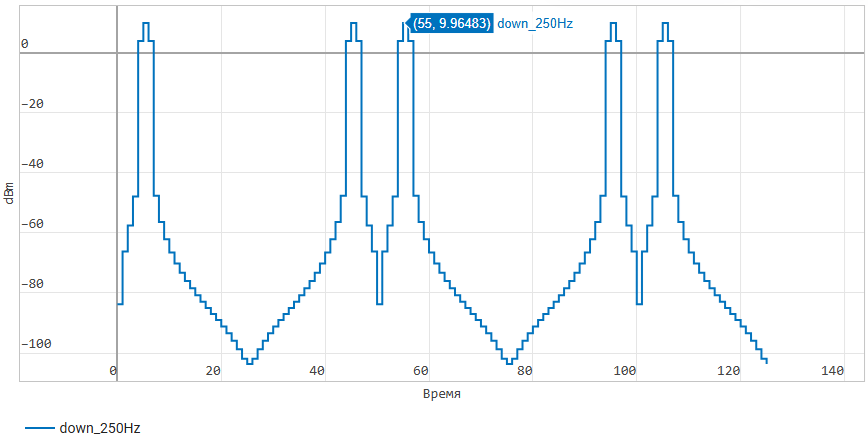
It is the presence of spectral copies in the output signal
that determines its shape - outliers with zeros. In fact, this
is a complex periodic signal formed by the sum of the basic signals -
sinusoids.
We can't eliminate them completely, but we can suppress
them with a proper low-pass filter. This filter
is called an anti-imaging or anti-aliasing filter.
It is always placed after surgery. Upsample and before
the operation Downsample.

Low-pass filter development

Our task is to develop a suitable prototype (specification)
of the filter and place its coefficients
in the block Discrete FIR Filter.

Taking into account that the initial signal can range
from 0 to 50 Hz, we select the filter cutoff frequency of 50 Hz,
the Kaiser window function, the normalized
transition bandwidth, as well as the required suppression
in the barrier band. Also note that
we select the specification for a sampling frequency of 500 Hz,
since this is the signal that enters the filter input.:

using DSP;
fs = 500;
mywindow = FIRWindow(; transitionwidth=0.15, attenuation=60, scale=true);
myFIR = digitalfilter(Lowpass(2*50/fs), mywindow);

Now we will calculate and display the amplitude-frequency
response (frequency response) of the filter to make sure that it
ability to suppress spectral copies above 50 Hz:

myTransferFunction = PolynomialRatio(myFIR,1);
H, w = freqresp(myTransferFunction);
freq_vec = fs*w/(2*pi);
plot(freq_vec, pow2db.(abs.(H))*2, linewidth=3,
     xlabel = "Частота, Гц",
     ylabel = "Амплитуда, дБ",
     title = "АЧХ фильтра нижних частот",
     ylim = (-120, 10))

A 50th order filter was synthesized according to the selected specification.
The shape of its frequency response, although it does not perfectly skip all
the frequencies we are interested in, but it is suitable for the current task of suppressing interfering ones. The filter coefficients
are already embedded in the model block, so you won't have to transfer them again.

Applying a low-pass filter

In the model, we right-click
on the filter block and select Включить блок.
After that, we run the model again for simulation,
and look at the spectrum of two signals - at the input and output
of the filter.:

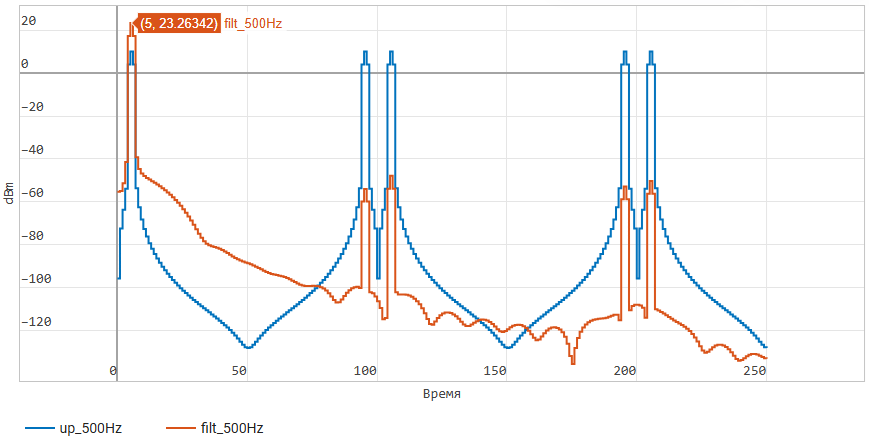
As we can see, the spectral copies are suppressed relative
to the 5 Hz sine wave by more than 70 dB. You can also notice that
the sine wave at a frequency of 5 Hz in the output signal has a
higher power. We specifically multiply the filter coefficients by 5,
because adding zeros is an operation. Upsample reduces
the energy of the signal by exactly 5 times.

Now let's look
at the shape of the output signal in the time domain:

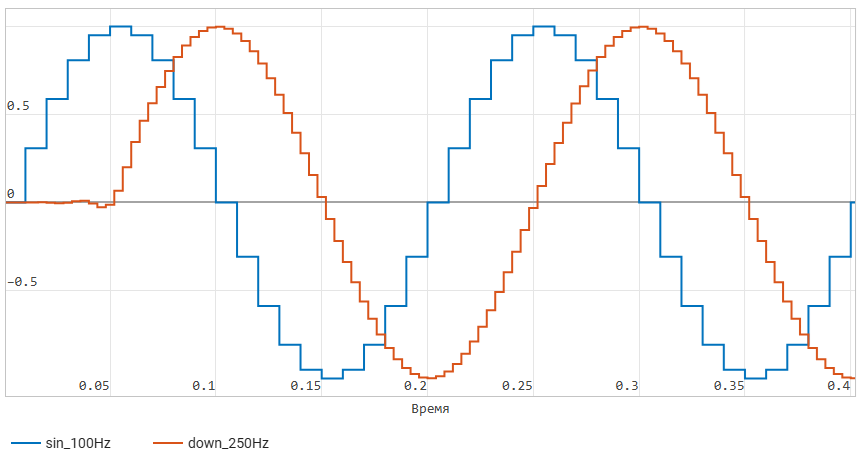
It corresponds in amplitude to the input signal, also has
a fundamental frequency of 5 Hz, its sampling frequency is 250 Hz,
and its shape is now a sinusoidal oscillation.

But we also see that it is delayed relative to the input signal
by a quarter of the period. This is the effect of applying a long-range FIR filter.
50 counts - such filters will necessarily introduce a delay.

Conclusion

In this example, we examined the basic principles of changing
the sampling rate in digital devices, the effects of imaging and aliasing,
and the need to use low-pass filters.