Engee documentation
Notebook

Verilog-implementation of 4-FSK character encoding (without FM)

Here we will look at working with 4-FSK (Frequency Shift Keying) in Engee.

Frequency modulation is a type of modulation in which information is encoded by changing the frequency of a signal. 4-FSK, four-level frequency manipulation, is a type of modulation used in DMR (Digital Mobile Radio), and it is optimal for use in PMR (Professional Mobile Radio) systems.

We will also generate the Verilog code from this model and test its performance in Vivado.

Verilog is a hardware description language used to develop electronic systems.

Verilog is needed in the design, verification, and implementation of analog, digital, and mixed electronic systems at various levels of abstraction.

Declare auxiliary functions

In [ ]: 
function run_model( name_model)
    Path = (@__DIR__) * "/" * name_model * ".engee"
    
    if name_model in [m.name for m in engee.get_all_models()] # Проверка условия загрузки модели в ядро
        model = engee.open( name_model ) # Открыть модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
    else
        model = engee.load( Path, force=true ) # Загрузить модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
        engee.close( name_model, force=true ); # Закрыть модель
    end
    sleep(0.01)
    return model_output
end
Out[0]:
run_model (generic function with 1 method)

Model analysis

We will study two variants of the model. One uses the standard selection logic implemented by switching. The second version of the block is implemented using a mathematical formula. Using such methods, it is often necessary to change algorithms beyond recognition when developing systems in order to optimize their performance in terms of speed or resources.

The table below is based on which the model was developed.

In [ ]: 
symbol = [-3, -1, 1, 3]
bits = [[0, 0], [0, 1], [1, 0], [1, 1]]

println(join(["bits: $bit, symbol: $f" for (f, bit) in zip(symbol, bits)], "\n"))

bits: [0, 0], symbol: -3
bits: [0, 1], symbol: -1
bits: [1, 0], symbol: 1
bits: [1, 1], symbol: 3

The screenshots below show the developed model.
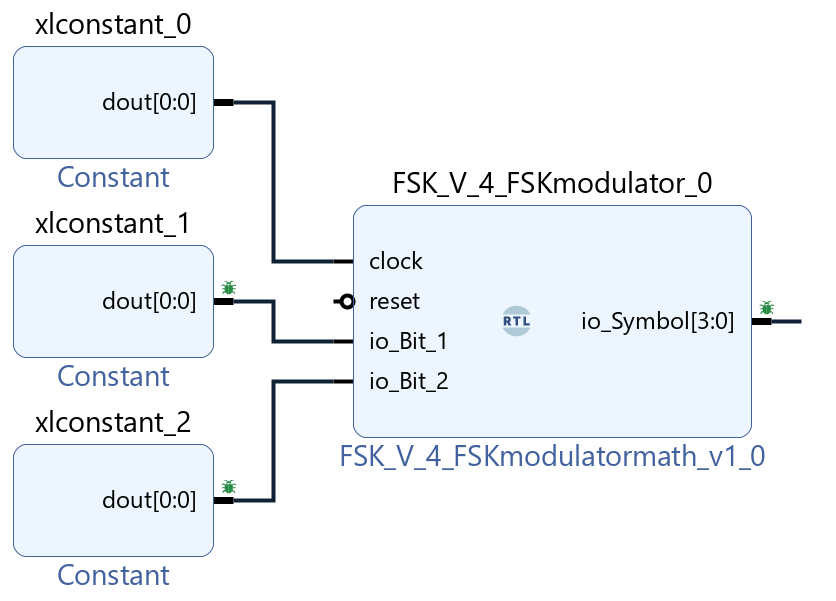
image.png

The source block is 4-FSK.
image.png

As we can see, there is significantly less logic in the block implemented using the formula than in the original block. In addition, all multiplication blocks in it use multiplication by 2, and, accordingly, when generating code, such logic will be a one-bit shift.

image.png

We can also note that shorter data types are used in this case than in the case of the original block, where Int8 was used.

Let's briefly touch on the topic of fixed-point data types. This data type is set by the command fi(X, 1, 16, 5), where from left to right the parameters are:

  1. Number values;
  2. sign (1-signed, 0-unsigned);
  3. Full word size;
  4. The size of the fractional part.

Next, let's look at a simple example.

In [ ]: 
x = fi(7.5, 1, 7, 5)
y = fi(7.5, 1, 7, 3)
println("x: $x")
println("y: $y")

x: 1.96875
y: 7.5

As we can see, in the first case, the number 7.5 went into overflow.

In [ ]: 
x+y
Out[0]:
fi(9.46875, 1, 10, 5)

You can also see that when these two numbers are added together, more memory is allocated for them than was originally allocated.

Checking the model's operability

Now let's analyze the correspondence of the two implementations with each other. First, let's run the model.

In [ ]: 
bit_1 = 1; bit_2 = 1;
println("Inp_bit: $([bit_1, bit_2])")

println()
@time run_model("FSK_V") # Запуск модели.

Inp_bit: [1, 1]

Building...
Progress 0%
Progress 7%
Progress 16%
Progress 26%
Progress 34%
Progress 43%
Progress 49%
Progress 59%
Progress 66%
Progress 72%
Progress 80%
Progress 86%
Progress 96%
Progress 100%
Progress 100%
  3.472636 seconds (81.98 k allocations: 6.529 MiB)
Out[0]:
SimulationResult(
    "4-FSK modulator math.Symbol" => WorkspaceArray{Fixed{1, 4, 0, Int8}}("FSK_V/4-FSK modulator math.Symbol")

)

Now let's compare the results. As we can see, both results correspond to the original table.

In [ ]: 
Symbol_math = collect(Symbol_sim).value[end]
println("Symbol_math: $Symbol_math")
Symbol_switch = collect(Symbol_sim_switch).value[end]
println("Symbol_switch: $Symbol_switch")

Symbol_math: -1.0
Symbol_switch: -1

To verify the final project, we can present the block from which we will continue to generate the code in the form of a formula. Let's make sure that the formula is identical to the model.

In [ ]: 
Symbol_ref = 2 * (2 * bit_1 + bit_2) - 3
println("Symbol_ref: $Symbol_ref")
println("Symbol_sim: $Symbol_math")

Symbol_ref: -1
Symbol_sim: -1.0

Let's generate the code from the 4-FSK modulator block

Let's start with the code generation command. Below is information about the possibilities of using the generator.

In [ ]: 
? engee.generate_code
Out[0]:

? engee.generate_code

Now let's set the target platform in the model.

image.png

Let's run the code generation. Due to the fact that the target platform is explicitly set in the model settings, we will not need the target selection line.

In [ ]: 
engee.generate_code(
"$(@__DIR__)/FSK_V.engee",
"$(@__DIR__)/V_Code",
subsystem_name="4-FSK modulator math",
# target="verilog"
)

[ Info: Generated code and artifacts: /user/my_projects/Demo/A_In_Work/Seminar/FSK/V_Code

Working with Vivado

Now let's test the received code in Vivado and download the received files.

image.png

Create an empty project.

image.png

Add the generated file.

image.png

Let's define the target platform for our project.

image.png

Now we can look at the final schematics of our project. It turned out to be very simple.

image.png

Let's synthesize and implement the project. As we can see, timings are not defined. This is due to the fact that the input ports of our block are empty, nothing is being supplied to them.

image.png

We can verify this by looking at the simulation results as well. All inputs and outputs are undefined.

image.png

Let's fix this and add a binding to our block by setting the input ports as constants.

image.png
image.png

Now let's repeat the simulation.

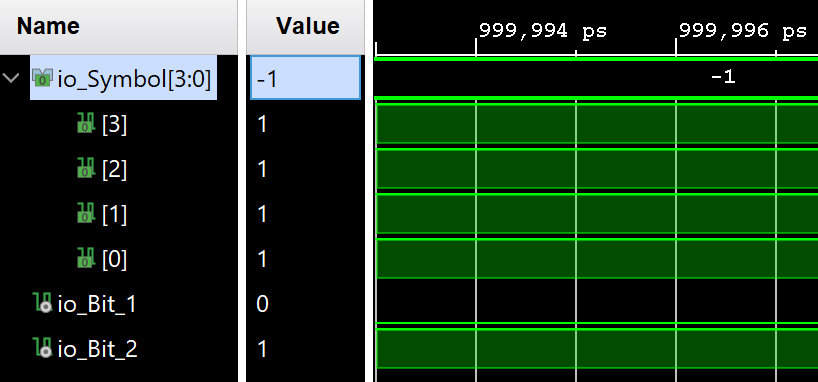
image_2.png

The result of the simulation may seem incorrect, but let's analyze the generated logic point by point, provided that a pair of bits [0,1] is received at the input. Let's start by analyzing the results using the formula we have developed.

In [ ]: 
Symbol_ref = 2*(2*0+1)-3 #[0,1]
println("Ожидаемый результат: $Symbol_ref")

Ожидаемый результат: -1

Now let's move on to our code:

(io_Symbol = {{1'h0, io_Bit_1, 1'h0} + {2'h0, io_Bit_2}, 1'h0} - 4'h3)

  1. {1'h0, 0, 1'h0}: 000
  2. {2'h0, 1}: 001
  3. {0,0,0} + {0,0,1}: 001
  4. {001, 0}: 0010
  5. 4'h3: 0011

Now let's move on to the answer. If we take bit subtraction, the result is: [1111].

  1. 0010 - 0011 = -1
  2. We take the module: 1: 0001
  3. Invert the bits: 0001: 1110
  4. Add 1: 1110 + 1: 1111

Based on the theses described above, it can be argued that our simplified implementation of the 4-FSK modulator works correctly.

Conclusion

In this example, we analyzed the possibilities of generating and verifying Verilog code in Engee, and made sure that this approach to developing FPGA systems is applicable and relevant. Moreover, it can significantly speed up the development process due to the ability to instantly edit and test the model.