Engee documentation
Notebook

Binary logic

In this example, we explore the application of binary logic to solve logical problems using an equation written in the Julia programming language and its implementation in a model.

Binary logic is a form of logic based on working with two states: true (1) and false (0). It is used to describe and solve problems where the results can be expressed in terms of "yes" or no. Binary logic is widely used in computer systems, digital electronics, and programming.

Logical tasks are tasks whose solution involves the use of logical operations such as "AND" (AND), "OR" (OR), "NOT" (NOT) and their combinations. Such tasks often arise in the field of automation, digital circuit design, and programming.

The example demonstrates how to combine the theoretical basis (the logical equation in Julia) with its practical implementation in models, allowing you to visually explore and analyze the process of solving logical problems.

Description of the binary equation

Let's set the states of our system, which in this case will be three:
𝐴, 𝐵 and 𝐶. At the same time, the condition
𝐴 will be determined randomly: if a random value is
𝑋 is greater than 0.5, then 𝐴 is true, otherwise false.

In [ ]: 
X = rand()
println("X = $(X)")
A = X > 0.5
println("A = $(A)")

X = 0.7960830917866893
A = true
In [ ]: 
B = false
C = true
println("B = $(B)")
println("C = $(C)")

B = false
C = true

Now let's move on to the description of the equation.
Let's assume that our logic is defined by the following equation: Z = ((A and B) or (C and B)).

In [ ]: 
Z = ((A && B) || (C && B))
println("Z = $(Z)")

Z = false

Now, using this equation, we will build a model and compare the simulation results and the results obtained in the model.
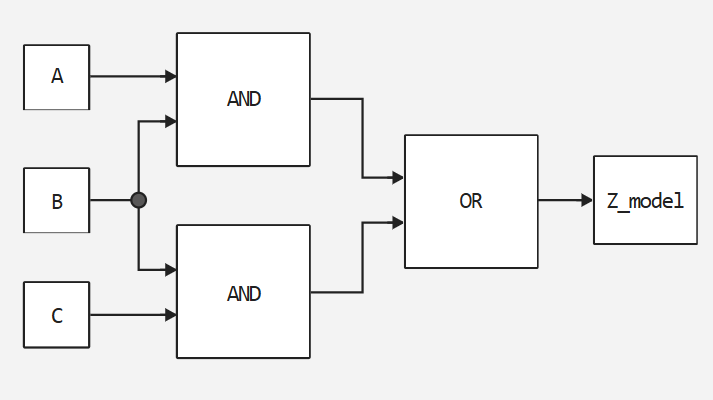
image.png

Auxiliary functions

In [ ]: 
# Enabling the auxiliary model launch function.
function run_model( name_model)
    
    Path = (@__DIR__) * "/" * name_model * ".engee"
    
    if name_model in [m.name for m in engee.get_all_models()] # Checking the condition for loading a model into the kernel
        model = engee.open( name_model ) # Open the model
        model_output = engee.run( model, verbose=true ); # Launch the model
    else
        model = engee.load( Path, force=true ) # Upload a model
        model_output = engee.run( model, verbose=true ); # Launch the model
        engee.close( name_model, force=true ); # Close the model
    end
    sleep(5)
    return model_output
end

Binary logic modeling

In [ ]: 
run_model("Logical_Operator") # Launching the model.
Z_model = collect(Z_model)
println("Z_model = $(Z_model.value[1])")

Building...
Progress 100%
Progress 100%
Z_model = false

We will perform the verification by comparing the simulation results and the results obtained during calculations in Engee.

In [ ]: 
println((Z_model.value[1]) == Z ? "Verification completed" : "The results didn't match")

Проверка пройдена

Conclusion

As a result of the research, the work of binary logic was demonstrated using the example of an equation implemented on Julia and in the model. The set system states (𝐴, 𝐵, 𝐶) are correctly processed, and logical operations are performed according to the description. The check showed that the model and code match, and the system functions without errors.

Blocks used in example