The concept of an algebraic loop¶
Algebraic loops (loops) occur when a feedback system contains only direct-pass blocks in the feedback loop. Direct-pass blocks are those that use the input value of the current time step to calculate the output value at the current time step. Thus a closed loop containing only direct-pass blocks creates a cyclic relationship between the output and input values of the blocks in a single time step.
Examples of direct-pass blocks are:
- Gain (Gain)
- Multiplication (Product)
- Add (Add)
- Transfer Fcn
- State-Space with non-zero matrix $D$
Blocks that are not directly transferable maintain one or more state variables that store input values from previous time steps. For example, these are the Integrator Integrator and the Delay Delay.
Consider a model that contains a sum block. It subtracts the output value of the block $x_a$ from the input value $u$.
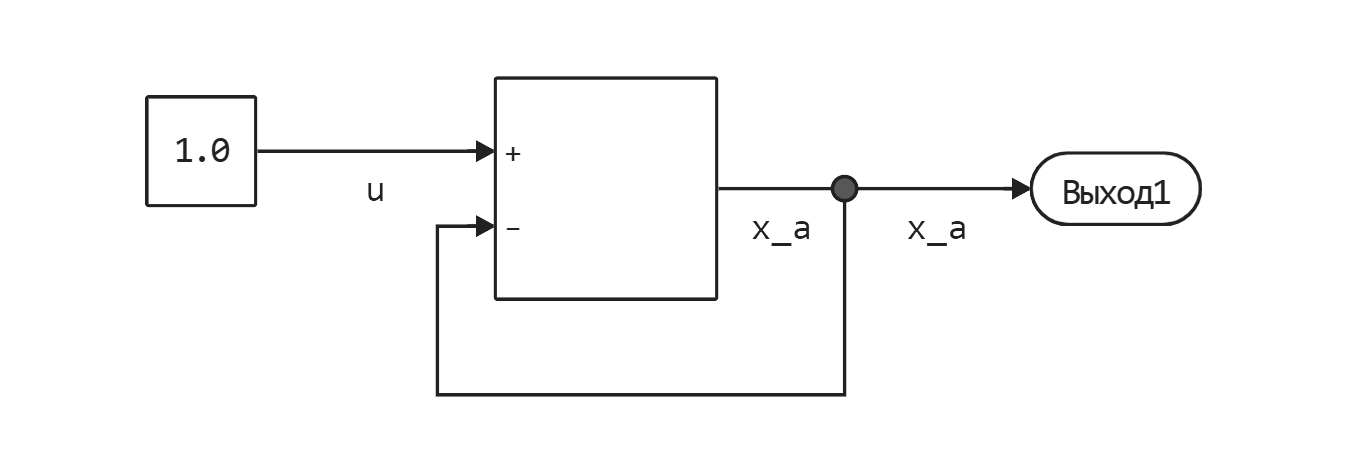
The model implements the following equation: $$ x_a = u - x_a $$
As you can see, there is an algebraic loop. And the solution in this case will be simple - rewrite the equation:
$$ x_a = u/2 $$
Mathematical interpretation¶
Engee has numerical solvers for simulating Original Differential Equations (ODEs). ODEs are systems of equations that can be written in the form:
$$ \dot{x}=f(x,t) $$
where $x$ is the state vector and $t$ is the independent time variable.
Some systems of equations include additional constraints that include the independent variable and the state vector, but not the derivative of the state vector. Such systems are called differential algebraic equations (DAEs).
The term "algebraic" refers to equations that have no derivatives. You can express differential equations in partial derivatives:
$$ \dot{x}=f(x,x_a,t) $$ $$ 0=g(x,x_a,t) $$
Where:
- $f$ and $g$ can be vector functions;
- The first equation is a differential equation;
- The second equation is an algebraic equation;
- A vector of differential variables is a vector of differential variables. $x$
- The vector of algebraic variables is $x_a$
In the model, an algebraic cycle represents an algebraic constraint. Models with algebraic cycles define a system of differential algebraic equations. The algebraic cycle is solved numerically for $x_a$ at each simulation step using an ODE solver.
Consider this model implementing a simple system of differential equations. The inner loop is an algebraic constraint and the outer loop is a differential equation.
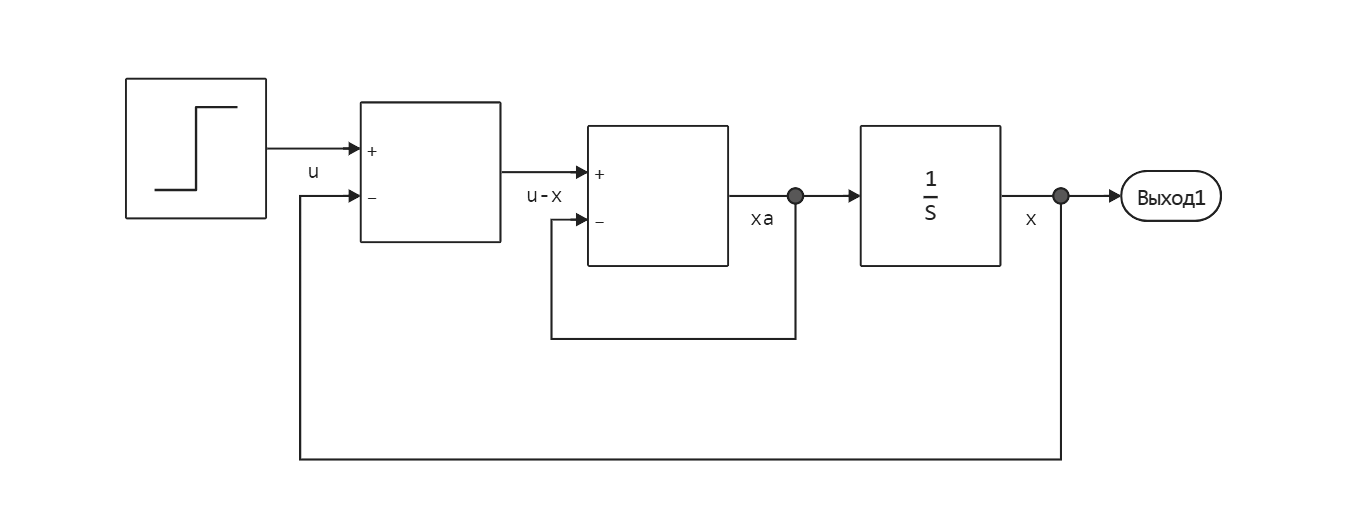
The model implements the DAU system: $$ \dot{x}=x_a $$ $$ 0=u-x-2x_a $$
For each step performed by the ODE solver, the algebraic loop solver must solve the algebraic constraint for $x_a$ before computing the derivative $\dot{x}$.
Artificial algebraic loops¶
Artificial algebraic loops can occur, for example, when atomic subsystems are used. Such systems implement a non-virtual hierarchy and are treated as separate units during the simulation. An atomic subsystem is executed for a given time step until every unit within the subsystem is executed before moving on to execute other units outside the subsystem.
Let's look at an example. Given a model which is a control system with a proportional object controller described by the
$$ G(s)=\frac{1}{s^2+2s+1} $$
The system has no algebraic variables, no feedback to the forward pass blocks, and contains no algebraic loop.
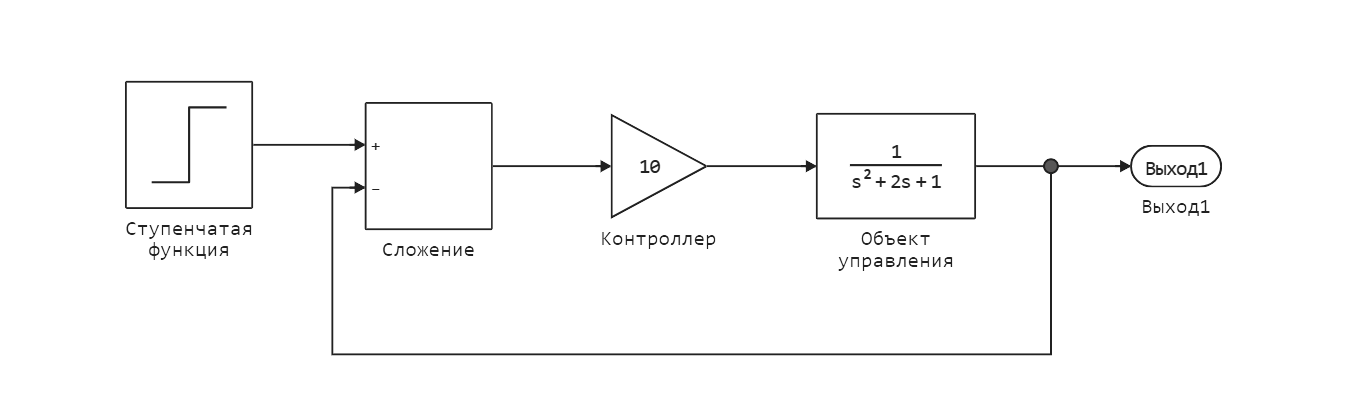
Open the model create_alg_loop.engee, as described in the following steps:
Enclose the controller and the control object in a subsystem.
Select "Convert to atomic unit" in the subsystem parameters to make the subsystem atomic.
Run the model.
You can also run the finished model atomic_alg_loop.engee.
As a result you will get an error:
When modelling this model, an algebraic loop occurs because the subsystem is straight even though the path within the atomic subsystem is not straight. The modelling stops due to finding an algebraic loop.
Conclusion¶
If your model contains an algebraic loop, you cannot simulate the model in Engee. You also cannot generate code from such a model. Algebraic loops should be avoided. How to do this is described in publication removing algebraic loops.