Advanced settings of the Engee Function block

The Engee Function block allows the user to embed their algorithm into the Engee model without redrawing it on primitives. At the same time, the user has full control over determining the behavior of the block.

Examples of such control methods are given below.

Overload of output parameters

Example: Conversion to a vector

It is required to implement a block that converts its input into a vector.

No login operations are required. The only thing required is to convert the input to a vector. To do this, calculate the length of the vector and get the type of its elements.

This task is implemented in the vectorize_it model by the VectorizeIT block.

Consider the code of this Engee Function. We are interested in the block functor and the method of redefining the dimensions and type of output.

Let's start with the definition of the functor:

function (c::Block)(t::Real, cache, in1)
	if in1 isa AbstractVector
		cache .= in1
	elseif in1 isa AbstractArray
		cache .= vec(in1)
	elseif in1 isa Real
		cache[1] = in1
	end
end

Here you should pay attention to the cache variable. This variable is declared for the Engee Function block if the setting is enabled. Use external cache for non-scalar output:

This setting is only available if the block has only one output.

Next, we will consider the definition of the dimension and type of the output signal. You can define them individually by selecting the Override type inheritance method and Override dimensions inheritance method options. However, it is possible to define them in a single function. To do this, select Use common method for types and dimensions inheritance (the choice will become available after enabling both methods):

The latter option is most appropriate for this case. Consider the code of this method:

function propagate_types_and_dimensions(inputs_types::Vector{DataType}, inputs_dimensions::Vector{<:Dimensions})::Tuple{Vector{DataType}, Vector{<:Dimensions}}
	in1t = inputs_types[1]
	in1d = inputs_dimensions[1]
	outd = (prod(in1d), )
	return ([eltype(in1t)], [outd]);
end

The input receives two vectors: the types of inputs and their dimensions. A tuple consisting of two vectors should be formed at the output:

• a vector of the data types of the output signals
• vector of output signal dimensions

It should be noted separately that the dimension is passed as a tuple (that is, as well as the result of the function size()), and the data type as the element type. In our case, it won't be Vector{eltype(in1t)}, and just eltype(in1t).

Strict block typing and caching of results

Example: Calculation of the system of equations

The Julia language allows you to dynamically allocate memory, but this slows down the code. Therefore, the Engee Function block can have a negative impact on the simulation speed. This example demonstrates how to maximize the performance of the Engee Function block.

Using a separate variable to store the result of the block operation (cache) allows you to get rid of dynamic memory allocation and significantly speeds up the block operation. Let's take a simple example:

As can be seen from the example, using a cache is an extremely desirable practice. For the Engee Function, we can define the cache in two ways:

1. By specifying the checkbox Use external cache for non-scalar output (for one output)
2. Manually creating caches in the block definition

To achieve maximum performance, all fields in the block structure must have a specific type and a fixed size.

As an example, consider the cached_calcs model and the ComputingTypesRuntime block.

This block implements the following system of equations:

The implementation of this system involves the use of caches, since the inputs can be non-scalar.

To create caches, we need to define a typed structure. The usual Define component structure method does not allow this, but we can enable the Use common code setting and create a structure for the block in the "common" code. The block structure definition code will be as follows:

struct Block{CacheType1,CacheType2} <: AbstractCausalComponent
	c1::CacheType1;
	c2::CacheType2;
  
	function Block()
	  sz1 = OUTPUT_SIGNAL_ATTRIBUTES[1].dimensions;
	  sz2 = OUTPUT_SIGNAL_ATTRIBUTES[2].dimensions;
	  type1 = OUTPUT_SIGNAL_ATTRIBUTES[1].type;
	  type2 = OUTPUT_SIGNAL_ATTRIBUTES[2].type;
  
	  c1 = isempty(d1) ? zero(t1) : zeros(t1, d1)
	  c2 = isempty(d2) ? zero(t2) : zeros(t2, d2)
  
	  new{typeof(c1), typeof(c2)}(c1,c2);
	end
  end

It should be noted that the type and dimension of the caches are derived from the output signals. And the attributes of the output signals are output in the Use common method for types and dimensions inheritance using a single calculation of the system of equations:

function propagate_types_and_dimensions(inputs_types::Vector{DataType},
 			inputs_dimensions::Vector{<:Dimensions})
			::Tuple{Vector{DataType}, Vector{<:Dimensions}}
	in1t = inputs_types[1]
	in2t = inputs_types[2]
	in1d = inputs_dimensions[1]
	in2d = inputs_dimensions[2]
	mockin1 = zeros(in1t, in1d)
	mockin2 = zeros(in2t, in2d)
	mockout1 = sin.(mockin1) .+ cos.(mockin2)
	mockout2 = mockin1 .+ mockin2
	return ([eltype(mockout1), eltype(mockout1)], [size(mockout1), size(mockout1)])
end

This technique will only result in a single memory allocation.

Direct feedthrough

Example: Breaking an algebraic loop

As an example, let's consider the practical problem of breaking an algebraic loop. It is recommended to break the algebraic loop using the delay block. But this technique leads to a distortion of the results. And the IC unit does not break the loop.

Therefore, we will create an Engee Function block that implements the following system of equations and breaks the algebraic loop:

To break the algebraic loop, we need to remove the direct feedthrough attribute. This can be done both from the settings of the Engee Function block, and programmatically by setting the Override direct feedthrough setting method option.

The example implementation is available in the loopbreaker model in the LoopBreaker block.

The principle of operation of the block is as follows: the parameter is set IC, which will be output at the time of initialization of the model, and at the initial time of the simulation. In the next steps of the simulation, the input of the block will be immediately transmitted to the output. Let's look at the implementation of this algorithm.:

The block is defined as:

struct Block{T} <: AbstractCausalComponent
    InCn::T
    function Block()
        InCn_t = INPUT_SIGNAL_ATTRIBUTES[1].type;
        new{InCn_t}(IC)
    end
end

And its functor is like:

function (c::Block)(t::Real, in1)
    if t<=0.0
        return c.InCn
    else
        return in1
    end
end

Additionally, the Override direct feedthrough setting method is defined. No logic or calculations are required here, so we just open the loop.:

function direct_feedthroughs()::Vector{Bool}
    return [false]
end

Let's make sure that the simulation is working correctly.:

Setting up Sample Time

Example: "Slowing down" the output

Such models and algorithms are possible, in which it is required to provide a certain period of updating the block outputs. In the case of the Engee Function block, the user has two methods for implementing such a requirement.:

• explicit indication of the sampling period through the block parameters
• Writing your own algorithm for determining the required period

In this example, the second option is considered.

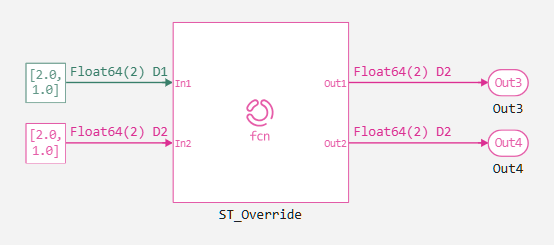
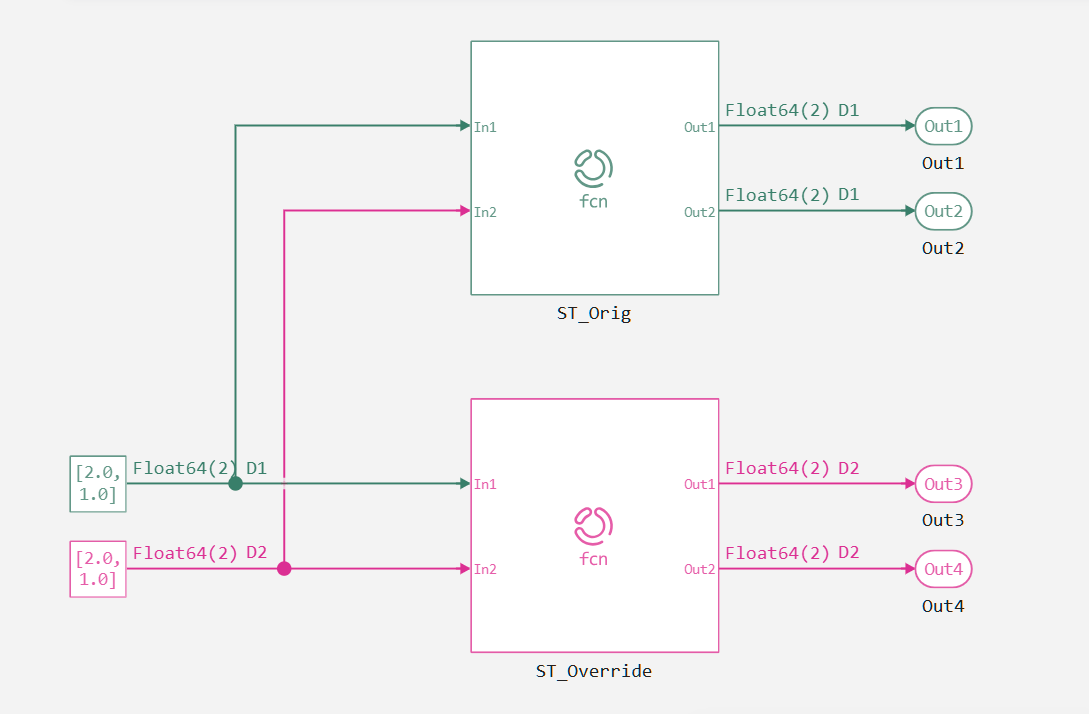
Consider the sample_time_override model:

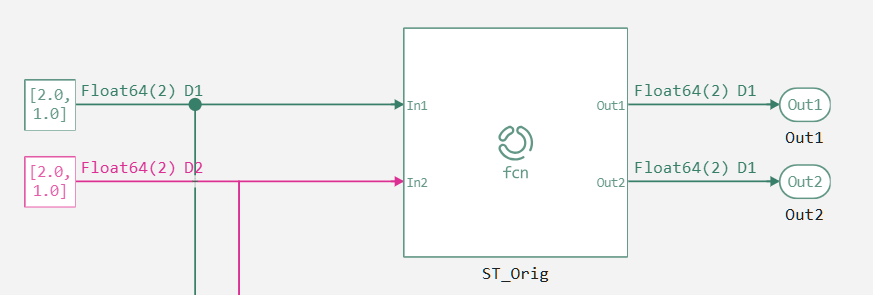
Functionally, the Engee Function ST_Orig and ST_Override blocks correspond to the algorithm from the Cache and strong typing section. However, now there is a requirement to produce the result with the lowest period. Let's look at how the built-in inheritance mechanism of the sampling period works.:

It can be seen that the period D1 is inherited, that is, the highest period. But the challenge is in D2 inheritance. To do this, we will include the Override sample time inheritance method section in the Engee Function code, and select the slowest period.:

function propagate_sample_times(inputs_sample_times::Vector{SampleTime},
         fixed_solver::Bool)::SampleTime

    max_period = argmax(t -> t.period, inputs_sample_times)
    return max_period

end

After the implementation of this method, the following result is obtained:

It can be seen that the desired period, D2, is now inherited.

important!

The first argument is a vector of named tuples of the SampleTime type, defined as:

SampleTime = NamedTuple{(:period, :offset, :mode), Tuple{Rational{Int64}, Rational{Int64}, Symbol}}

The mode field of this tuple takes the following values: :Discrete, :Continuous, :Constant, :FiM.

The second argument is a flag that shows the solver class. If the flag is true, then a constant-step solver is selected.

Conclusions

The methods of advanced programming of the Engee Function block were considered. These methods allow you to determine in detail the required block behavior and achieve maximum performance. This article does not cover typical errors when writing block code and techniques for writing secure code.