Engee documentation
Notebook

The Van der Pol oscillator

This example shows how to model the second-order Van der Pol differential equation (VDP) in Engee. In dynamics, the oscillator is non-conservative and has nonlinear attenuation. At high amplitudes, the generator dissipates energy. At low amplitudes, the generator generates energy.

The oscillator is given by a second-order differential equation:

image.png

where:

  1. x is the position relative to time.
  2. t - time
  3. Mu — attenuation.

The VDP generator is used in biological and physical sciences, including in electrical circuits.

Next, let's move on to the implementation – we'll declare the model launch function and connect the necessary libraries.

In [ ]: 
 using Plots

 function run_model(name_model)
    Path = (@__DIR__) * "/" * name_model * ".engee"

    if name_model in [m.name for m in engee.get_all_models()] # Проверка условия загрузки модели в ядро
        model = engee.open( name_model ) # Открыть модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
    else
        model = engee.load( Path, force=true ) # Загрузить модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
        engee.close( name_model, force=true ); # Закрыть модель
    end

    return model_output
end
Out[0]:
run_model (generic function with 1 method)

Let's run a model with several options for the Mu value. Next, in the figure, you can see the model that we made based on the formula described above.

image.png

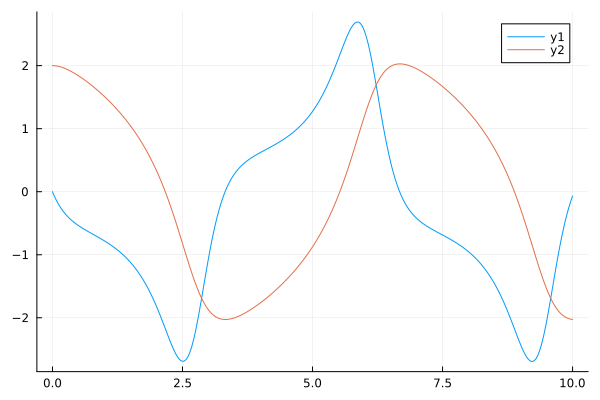
The attenuation coefficient is equal to one

Let's set the Mu and run the model, and then analyze the aggregated data.

In [ ]: 
Mu = 1;
run_model("vdp")
sleep(5)
collect(simout)

Building...
Progress 100%
Out[0]:
2-element Vector{WorkspaceArray}:
 WorkspaceArray("vdp/Integrator.1")
 WorkspaceArray("vdp/Integrator-1.1")
In [ ]: 
# Скорость
v = simout["vdp/Integrator.1"];
v = collect(v);
plot(v.time, v.value)

# Положение
p = simout["vdp/Integrator-1.1"];
p = collect(p);
plot!(p.time, p.value)
Out[0]:

As we can see from the resulting graph, at Mu = 1, the VDP generator has nonlinear attenuation.

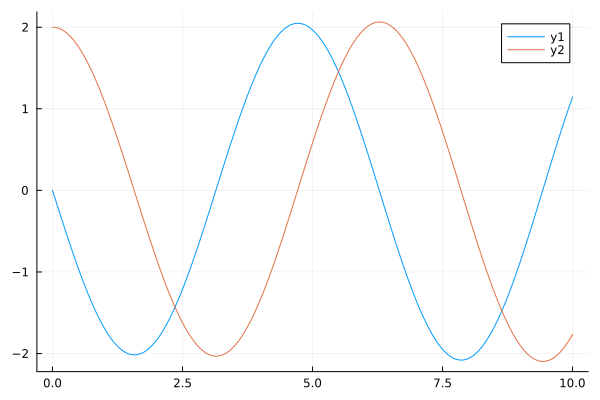
The attenuation coefficient is zero

Let's set the Mu and run the model, and then analyze the aggregated data.

In [ ]: 
Mu = 0;
run_model("vdp")
sleep(5)
collect(simout)

Building...
Progress 100%
Out[0]:
2-element Vector{WorkspaceArray}:
 WorkspaceArray("vdp/Integrator.1")
 WorkspaceArray("vdp/Integrator-1.1")
In [ ]: 
# Скорость
v = simout["vdp/Integrator.1"];
v = collect(v);
plot(v.time, v.value)

# Положение
p = simout["vdp/Integrator-1.1"];
p = collect(p);
plot!(p.time, p.value)
Out[0]:

Analyzing the graph, we can conclude that at Mu = 0, the VDP generator has no attenuation, energy is conserved, and the differential equation itself takes the following form:

image.png

Conclusion

In this example, we modeled the second-order Van der Pol differential equation in Engee and looked at how it works with different values of the attenuation coefficient.

Blocks used in example