Engee documentation
Notebook

Creating Engee Function blocks with state variables

In this example, we will create a block Engee Function, the parameters of which can change over time depending on various factors. Usually, the output data of a user block is calculated based on the input data and the time vector. But in this example, we will show how to work with variables that can store the internal state of a block.

In practical terms, we will show how to change the result of calculating a user block depending on the internal execution counter implemented inside the block.

Organizing the parameters of the Engee Function block

Block Parameters Engee Function you can set it in different ways:

  • using constants, through the settings window Parameters
  • using variables from the global variable space Engee (visible in the Variables Window)
  • using the internal parameters of the block specified in its code (and their lifetime is not limited to the next calculation cycle, but is equal to the lifetime of the model).

The first two options are implemented almost identically. If the number of parameters is non–zero, then you need to set a name for each of them. Name and the value Value.

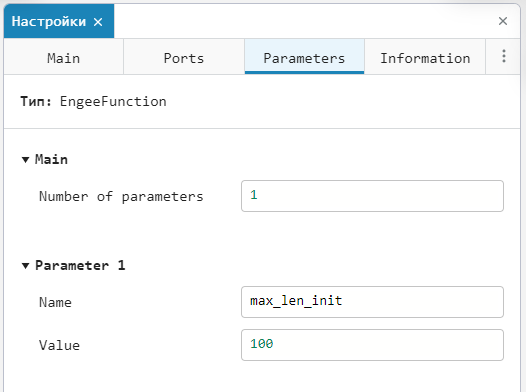
image_3.png

Here we have set the window size for calculating statistical parameters. max_len_init and assigned it a value 100.

We could assign it a value N, set in the global variable space. Keep in mind the limitation of the model compiler: when passing a variable from the global space, the parameter name (Name) should not be identical to the name of a global variable (Value).

image_2.png

This temporary compiler behavior will be fixed soon.

Variable parameters in the Engee Function code

Let's take a practical example. We are going to implement a block that calculates the statistical parameters of the part of the sample that falls within a sliding window of a given size. The window will be initialized to zero, so the first N results will be offset, but then we will see statistics on a sliding window that includes the last N values from the observed sample.

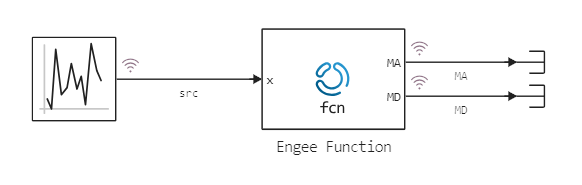
Block Engee Function it will accept scalar values as input and accumulate statistics on them. The input will contain a noise generation unit, a uniformly distributed random variable with values in the range (-1.1). The interface of the block will look like this:

image_2.png

Here MA means Moving Average (moving average), and MD – Moving Deviation (sliding variance).

It is worth commenting on each section of the code that defines the behavior of our custom block.

The code begins with initializing the structure of the user block. Title Block chosen randomly, it can be anything. Inside, we set several parameters:

  • i – the counter of the last added item in the cyclic storage
  • max_len – the size of the sliding window
  • X – sample accumulator (vector size max_len)

In the function Block() the internal parameters receive specific values, including those obtained from the outside (window size max_len_init it is set on the tab Parameters).

Parsing the code inside the Engee Function component

It is worth carefully approaching the issue of assigning data types to block parameters. If you do not declare the data structure defining the state variables as a structure of the type mutable, then all the "simple" types in the structure will be unchanged (you will have to use vectors or references, for example i :: Ref{Int32};). We want the parameters to be able to be changed. Therefore, we set a special modifier for our structure.:

mutable struct Block <: AbstractCausalComponent

    i :: Int32;
    max_len :: Int32;
    X :: Vector{Float64};

    function Block()
        return new( 1, max_len_init, zeros(Float64, max_len_init) )
    end

end

Then, in the code, we see a function that is calculated each time the block is accessed.

It is very important that when accessing this function, its internal variables do not change. Method (functor) step It can be called many times between simulation steps, so if you change the internal state of the block, it will change too often.

Here we can access the external and internal parameters of the block (c.параметр).

function (c::Block)(t::Real, x)

    # Local variables are needed for readability only
    X = c.X
    N = c.max_len

    MA = sum( X[1:N] )/N;
    MD = sqrt( sum( (X[1:N] .- MA).^2 ) / (N-1) )

    return (MA, MD)
end

And finally we see the function update!, which is designed to make changes to the block parameters c.

  • We substitute the current value x with the block entrance Engee Function in the vector X by index i;
  • Then we increase the index by 1 i, and when it reaches the value max_len, reduce it back to one;
  • And finally, we return the updated parameter structure. c to access it in the next iteration.
function update!(c::Block, t::Real, x)
    
    c.X[c.i] = x
    c.i = max(1, (c.i + 1) % (c.max_len-1))
    
    return c
end

The code inside update! This is especially important in cases where the block Engee Function it is in an algebraic loop (for example, it accepts its own outputs as input or has a parameter set direct_feedthrough=false). In models where there is no loop, everything can be done in the second block of code (the functor step).

Launching the model and discussing the results

Let's run this model using the software control commands:

In [ ]: 
mName = "engee_function_moving_average"
model = mName in [m.name for m in engee.get_all_models()] ? engee.open( mName ) : engee.load( "$(@__DIR__)/$(mName).engee" );
data = engee.run( mName )
Out[0]:
Dict{String, DataFrame} with 3 entries:
  "MA"  => 501×2 DataFrame…
  "src" => 501×2 DataFrame…
  "MD"  => 501×2 DataFrame…

Output the result:

In [ ]: 
using Plots, Formatting

p = plot( data["MD"].value, data["MA"].value, label="MA(MD)", linez=range(0.4, 1, length(data["MA"].value)), c=:blues, cbar=:none)
# Последняя точка на графике
scatter!( p, [data["MD"].value[end]], [data["MA"].value[end]], c=:cyan )
# Текстовая подпись к этой точке 
annotate!( p, data["MD"].value[end], data["MA"].value[end],
           text("MA=$(sprintf1("%.2f",data["MD"].value[end])), MD=$(sprintf1("%.2f",data["MA"].value[end]))  ", 8, :right ),
           legend=:none )

# Вывод двух графиков
plot(
    # График слева: шум
    plot( data["src"].time, data["src"].value, label="input", c=:red, legend=:none ),
    # График справа – зависимость мат.ожидания от дисперсии
    p,
    size=(800,300)
)
Out[0]:

The left graph shows the noise signal that was received at the entrance to the user block. Engee Function. The right graph shows the dependence of the moving average on the variance value for the sliding window.

It can be noted that the starting point of the mean and variance was the value for the null sample, but after a few dozen steps, the estimate of these parameters shifted to the point , . By the end of the billing period, when the initialization of the sliding window stopped affecting statistics, the point on the graph began to noticeably shift to zero mathematical expectation when .

Conclusion

If you add to the original template the code in the component Engee Function If there are several standard designs, then this component can embody very complex behavior based on external code and mutable parameters. In Engee, there are many graphical and textual ways to describe the behavior of models, in addition to which you can use dynamic blocks with custom code inside.

Blocks used in example