Engee documentation
Notebook

Using the Variant Source and Variant Sink blocks

In this example, we will show how the blocks work. Variant Source and Variant Sink. These blocks allow you to switch between different model implementations, which are generators of input data or consumers of output data of some subsystem.

Introduction

Suppose you need to calculate the operation of a model with different input sensors, different cyclograms, or different algorithms for filtering data at the output. For such testing, you can assemble several separate models, the number of which will quickly become impractically large. Or you can assemble all the models into one and switch the conditions using variables.

In this simplified example, the model configuration will be set by two scalar variables.:

In [ ]: 
Pkg.add(["Combinatorics"])
In [ ]: 
V = 1;
W = 1;

The model has several signal line switches controlled by external variables.

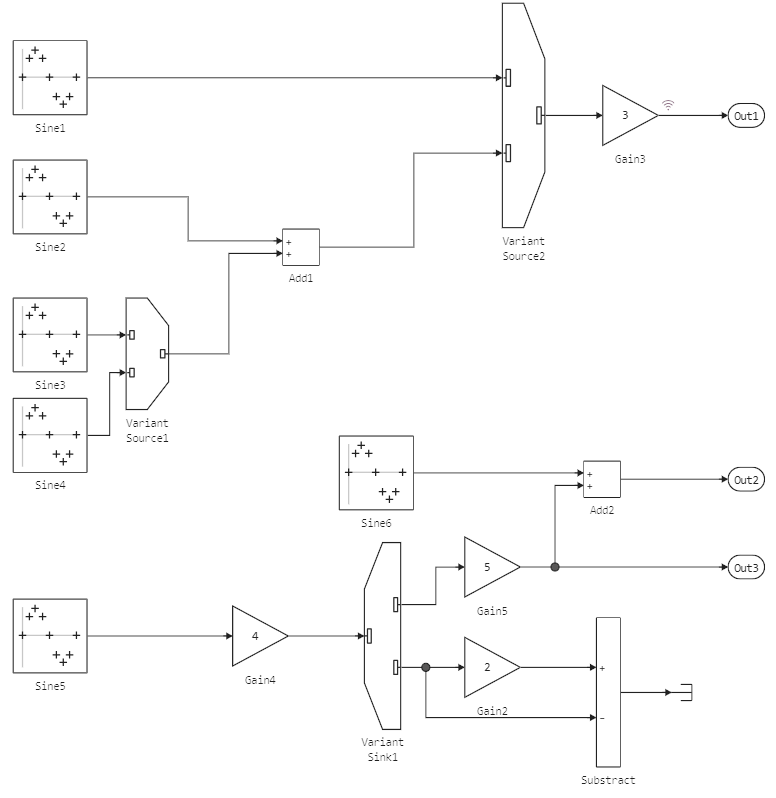
image.png

Signal selection conditions in each block Variant Source or Variant Sink they are set using expressions.

The expression that first takes the true value defines the port number through which the data will go from or to some subsystem. Let's interpret the different variants of the systems that are implemented in this scheme.:

  • If W==1 is the true expression of the Variant Source1 activates the input Sine3, and when V==4 the entrance is activated Sine4.
  • When V==1 block Variant Source 2 skips the signal from the block Sine1, and when V==2 – signal from the unit Add1.
  • If the block Add1 inactive, then Variant Source 1 It will also be inactive, and then the blocks will be disabled. Sine3 and Sine4 (block Sine3 active when V==2 && W==1, and the block Sine4 active when V==2 && W==2).
  • Yulok Gain3 active either when V==1, or when V==2; under other conditions (for example , when V=4) we will get an error because on the output port Out1 no output signal will be given.
  • Blocks at the exit Variant Sink1 they become active when W==1 (Gain5) or when W==2 (Gain2, Substract, Terminator).
  • Finally, the blocks Sine6, Sum and Out2 they are always active, they are not subject to the conditions for choosing system options. To ensure that these blocks are executed only under certain conditions, you can put blocks before and after them. Variant Source/Sink both with a single entrance and exit.

Under some combinations of conditions, this model returns an error because the subsystem's output ports must receive an active signal regardless of the subsystem's variant. It is not possible to send an active and inactive signal to any block at the same time, it is necessary to explicitly design the output ports of such a system using blocks Variant Source/Sink to set default values.

Running the script

In [ ]: 
mName = "variant_source_sink"
model = mName in [m.name for m in engee.get_all_models()] ? engee.open( mName ) : engee.load( "$(@__DIR__)/$(mName).engee" );
data = engee.run( mName )
Out[0]:
Dict{String, DataFrames.DataFrame} with 1 entry:
  "Gain3.1" => 51×2 DataFrame…
In [ ]: 
plot( data["Gain3.1"].time, data["Gain3.1"].value )
Out[0]:

Running multiple scripts

Now we will run several variants of the model in a loop, switching state variables in order to use a combination of input conditions to show how the system works in different scenarios.

In [ ]: 
using Combinatorics
In [ ]: 
# We will set all the input conditions we are interested in
vV = [1,2,4];
vW = [1,2,4];

# Loading the model
mName = "variant_source_sink"
model = mName in [m.name for m in engee.get_all_models()] ? engee.open( mName ) : engee.load( "$(@__DIR__)/$(mName).engee" );

# We will store the success of the execution in a matrix, which we initialize with the missing values.
run_success = NaN .* zeros(length(vV), length(vW))

# Let's go through all the combinations of input conditions and check if the model holds.
for c in combinations( vcat( vV,vW ), 2  )
    V,W = c[1],c[2]
    i = findfirst( vV.==c[1] )
    j = findfirst( vW.==c[2] )
    
    try
        # Let's run the model for execution
        data = engee.run( mName )
    catch e
        # If the model was executed with an error, write 0 to the output matrix.
        run_success[i,j] = 0
    else
        # We'll write one only if the catch condition didn't work.
        run_success[i,j] = 1
    end

end

Let's display a graph on which statistics on launches of different variants of our model will be collected.

In [ ]: 
gr()
# Output of a non-interactive map reflecting the success of the model
heatmap( run_success, xticks=(range(1,length(vV)), vV), yticks=(range(1,length(vW)), vW),
         xlabel = 'V', ylabel='W', title="Model execution success", yflip = true, cbar=false, c=:Blues )
# Annotation on top of each cell
annotate!( vec(tuple.((1:length(vV))', (1:length(vW)), string.(Int32.(run_success)))) )
Out[0]:

Conclusion

We have seen that several system variants can be assembled on one canvas. This method simplifies testing and allows you to generate many code variants at once to further automate semi-natural modeling.

Blocks used in example