Code placement in Engee Function blocks

Using blocks Engee Function you can create model elements that behave according to the algorithm you set. It makes sense to use these blocks in the following cases:

• If you already have the necessary, tested algorithm in the form of Julia code, or if it is easy for you to write it yourself;
• If it's easier to write an algorithm in Julia than to create it from graphical components;
• If the behavior of the block you need is not set by any of the existing Engee blocks, or it cannot be set using graphical blocks.

Blocks Engee Function can store calculate state variables, unlike blocks MATLAB Function MATLAB/Simulink environments. So they can also be used to replace blocks. S Function.

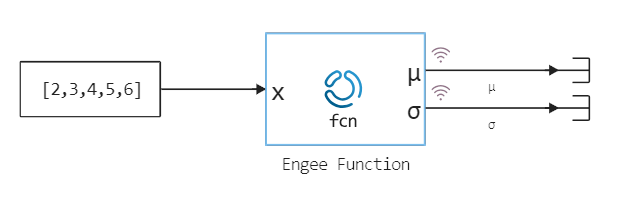
Let's calculate the mathematical expectation and variance of the vector using the Engee Function block.

Let's show you how to use the model Engee Function calculate the statistical characteristics of a vector of arbitrary length applied to the block input.

Based on the fact that the connection of additional libraries inside the blocks Engee Function (for example, Statistics.jl) is not supported, we implement calculations in the block according to the formulas:

where – mathematical expectation of the sample , – variance, – the number of items in the selection.

The following code allows you to implement these calculations (placed inside the block Engee Function):

struct Block <: AbstractCausalComponent; end

# Calculating the block output signals
# The first argument `t` - time, the rest are the values of the input signals
function (c::Block)(t::Real, x)
    N = length(x);
    μ = sum(x)/N;
    σ = sqrt( sum( (x .- μ).^2 ) / (N-1) )
    return (μ, σ)
end

We will calculate the variance with the Bessel correction (from here N-1).

You can enter or edit this code by opening the editor by clicking the "Edit Source code" button in the block settings. Engee Function (available when you double-click on the block or at the touch of a button for the selected block).

It is worth paying attention to the configuration of the inputs and outputs of this unit.

The three panels shown in the illustration show the properties of the block, the configuration of its input and output ports, and the settings of the parameters that are passed to the code.

• in the block properties (tab Main) you need to pay attention to the number of inputs and outputs – our example has one input and two output signals;
• in the port properties (tab Ports) we indicate that the input port is called x will have the dimension -1 (inherited from the previous block when compiling the model), the dimension of the two output signals with the names μ and σ specified as () – this is the dimension of a scalar;
• on the options tab" (Parameters) we only indicate that the block does not have additional parameters passed to the code (the number is equal to 0).

The signal dimension can be found using the command size. The terminal will tell you which dimension to specify when transferring to the block. Engee Function scalar, vector, or matrix.

We can specify the specific length of the input vector. (5,) observing the syntax of describing one - dimensional tuples (Tuple), or we can rely on the compiler and define the dimension of the input signal as inherited (equal to -1).

Let's put our block in the following environment (model engee_function_basics.engee):

Let's run the model using the Program Control commands and build a graph.:

The graph shows us that the mathematical expectation and variance of the sequence are [2,3,4,5,6] they are equal to the values 4.0 and 1.58.

Conclusion

To the block applications Engee Function The ones that we did not consider in this example are:

• adding external code saved in files *.jl, through directives include
• setting block parameters received from the global Engee variable space,
• changing block parameters, i.e. creating a block Engee Function with time-varying parameters.

You will find them in other demo examples.