Advanced block development based on Engee Function
Project Description
We have already learned how to develop our blocks using Engee Function.
But what if the algorithm to be implemented is complex and cumbersome? Problems arise immediately:
-
The Engee Function code turns out to be bloated and it's just hard to read.
-
It is unclear how to test such code. If an error occurs, it is difficult to localize it.
Solving these problems is not "rocket science", but routine work for programmers. So let's be them for a while!
This is how we will solve the problems of bulky code.:
-
Let's separate the algorithm into a separate module
-
We will cover the module with tests
-
Let's increase the stability of the code
As an example, consider an algorithm for finding the distance between two sets of observations. And to work, we will need the following packages:
import Pkg
Pkg.add(["LinearAlgebra", "Test", "BenchmarkTools"])
Code removal to the module
A module in the Julia context is code that is enclosed in a separate namespace. This allows you to make variables inside this module "invisible" outside it. To learn more about the advantages of the modules, please refer to help.
Let's look at the code of our algorithm enclosed in the module:
;cat PDIST2.jl
Testing
The purpose of testing is to prove that the code works correctly, and all exceptions are caught.
The tests are written using the [Test.jl] package(https://engee.com/helpcenter/stable/ru/julia/stdlib/Test.html )
Let's create three simple tests:
-
Simple function call
-
Processing of different dimensions
-
Correctness of calculating distances between identical matrices
Let's put these tests in a test suite, which is defined as:
@testset <setname> begin
<tests>
end
A special feature of the tests in the Test package.The jl is that testing macros verify the truth of a certain expression. Let's look at an example:
using Test, LinearAlgebra
demoroot = @__DIR__
include("PDIST2.jl")
X = rand(3,3)
Y = rand(3,3)
Z = PDIST2.EF_pdist2(X,Y);
@testset "EF_pdist2 tests" begin
@test_nowarn PDIST2.EF_pdist2(X,Y);
@test_throws DimensionMismatch PDIST2.EF_pdist2(rand(3,3),rand(2,2))
@test iszero(diag(PDIST2.EF_pdist2(X,X)))
end
Performance evaluation
To evaluate the overall performance of the code, you need to measure several indicators:
-
Speed of execution
-
Amount of allocated memory
-
Number of allocations (specific to Julia)
To do this, we will use the Benchmark.jl package. Its advantage lies in the fact that you can either fine-tune the experiment or start measuring immediately.:
using BenchmarkTools
@benchmark PDIST2.EF_pdist2(rand(10,10),rand(10,10))
The following measurements are important to us: Time and Memory estimate.
Time is the execution time of a single run. Since @benchmark runs several runs, we get a set of such measurements and can apply statistical processing to it. Its results are shown after running the @benchmark macro, as shown above.
Memory Estimate will show the amount of allocated memory. Let's see how the execution time and the amount of memory increases as the input volume increases.:
matrix_size = 80 # @param {type:"slider",min:10,max:100,step:10}
@benchmark PDIST2.EF_pdist2(rand(matrix_size,matrix_size),rand(matrix_size,matrix_size))
Failure tolerance
The code you create must be error-resistant. This requires working with exceptions.
An exception, in a general sense, is any error that can be handled. The main difference from the usual errors (syntactic ones) is that the user can generate exceptions himself. Let's look at the code of our pdist2 function:
m, n = size(X)
p, n2 = size(Y)
n == n2 || throw(DimensionMismatch("Number of columns in X and Y must match"))
If the dimensions of the matrices do not match, then the throw function is called and an exception is thrown.
The exception can be handled using the construction
try
catch
end
A code call is placed in the try block. If this code throws an exception, the code from the catch block will be executed.
Using the library in the Engee Function
As an example, we will use the EF_dist_find model.:
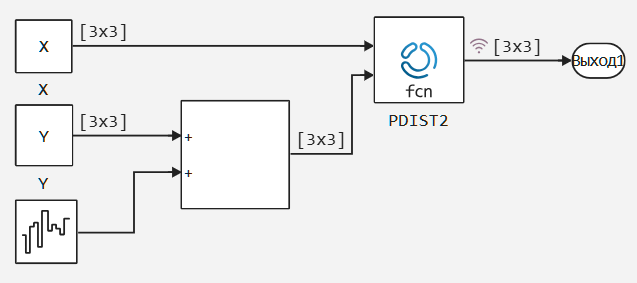
mdl = engee.open(joinpath(demoroot,"EF_dist_find.engee"));
Consider the PDIST2 block constructor:
include("/user/start/examples/base_simulation/advanced_block_development/PDIST2.jl")
mutable struct Block <: AbstractCausalComponent
cache::Matrix{Float64};
function Block()
c = zeros(Float64,INPUT_SIGNAL_ATTRIBUTES[1].dimensions);
info("Allocated $(Base.summarysize(c)) bytes for pdist2")
new(c)
end
end
We include our module in the Engee Function, specifying the full path to its code.
Using the info() function, we will display the amount of memory allocated when creating the cache.
Consider the Step method of this block:
function (c::Block)(t::Real, in1, in2)
try
c.cache = PDIST2.EF_pdist2(in1,in2);
catch
error("Matrix Dimensions should be equal!")
stop_simulation()
end
return c.cache
end
Note that the function call from our module is wrapped in an exception handler. If our pdist2 function throws an exception, the error "Matrix Dimensions should be equal!" will appear in the diagnostic window, and the simulation will be stopped.
When opened, two 3x3 matrices with random numbers are created. Let's make sure that the model works.:
engee.run(mdl)
Conclusions
The project showed an approach to creating an Engee Function-based block, which makes debugging easier and improves the quality and reliability of the code.