Comparison of DC/DC converter modeling techniques
Description
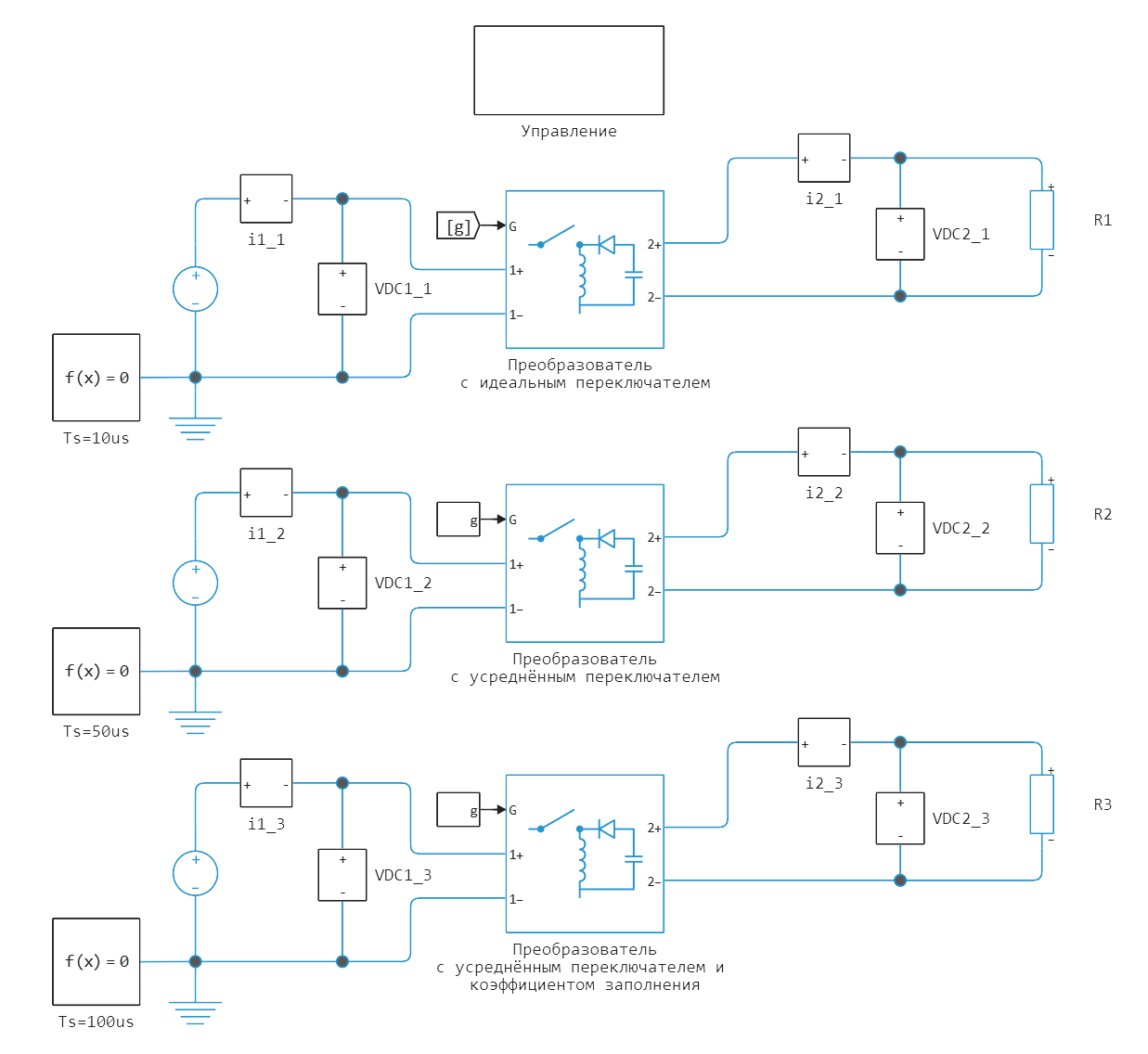
This example shows how to use various DC/DC converter modeling techniques. The control subsystem contains a PWM generator. The model contains three converters:
- A converter with an ideal switch — to achieve high detail, this model uses an ideal switch, with a sampling period of 10 microseconds.
- Converter with an average switch — to achieve high detail, even with a sampling period of 50 microseconds, this model uses an average switch with an average PWM signal.
- Converter with an average switch and a fill factor — to increase the sampling period and work as an ideal average converter, this model uses an average switch and a fill factor signal instead of a PWM signal, the sampling period is 100 microseconds.
Model
Simulation results
Loading the model:
model_name = "dc_dc_fidelity";
model_name in [m.name for m in engee.get_all_models()] ? engee.open(model_name) : engee.load("$(@__DIR__)/$(model_name).engee");
Launching the model:
results = engee.run(model_name);
To import the simulation results, logging of the necessary signals was enabled in advance and their names were set. Converting the simulation results from the results variable:
# simulation time vector
sim_time = results["i2_1"].time;
# vectors of recorded signals
i2_1 = results["i2_1"].value;
i2_2 = results["i2_2"].value;
i2_3 = results["i2_3"].value;
i2_en = hcat(i2_1,i2_2,i2_3);
i1_1 = results["i1_1"].value;
i1_2 = results["i1_2"].value;
i1_3 = results["i1_3"].value;
i1_en = hcat(i1_1,i1_2,i1_3);
v2_1 = results["v2_1"].value;
v2_2 = results["v2_2"].value;
v2_3 = results["v2_3"].value;
v2_en = hcat(v2_1,v2_2,v2_3);
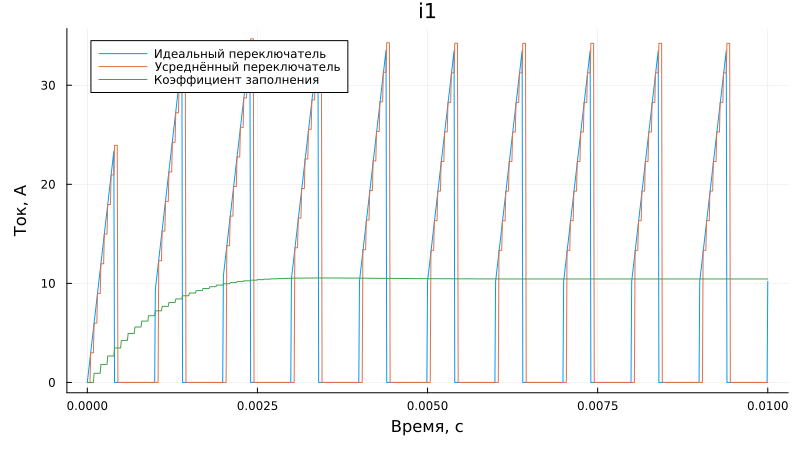
Graph of the current consumed by the converter (i1):
using Plots;
gr();
plot(sim_time, i1_1, label = "The perfect switch", xlabel = "Time, from", left_margin=5Plots.mm)
plot!(sim_time, i1_2, label = "The average switch", ylabel = "Current, A", bottom_margin=5Plots.mm)
plot!(sim_time, i1_3, label = "Fill factor", title = "i1", size = (800,450))
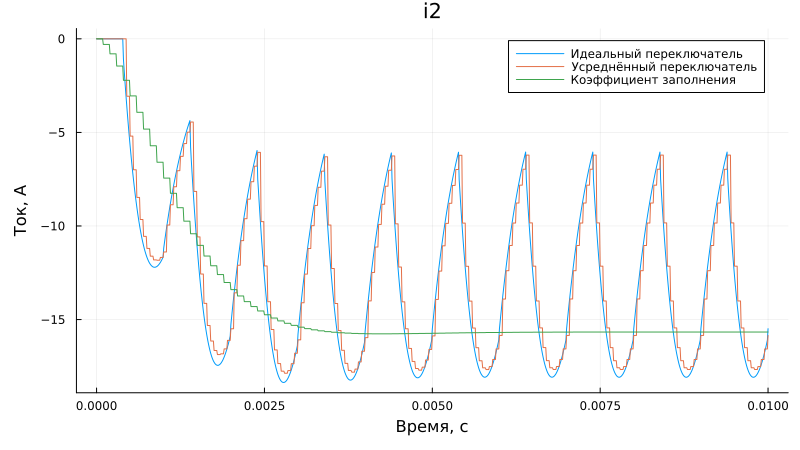
Load current graph (i2):
plot(sim_time, i2_1, label = "The perfect switch", xlabel = "Time, from", left_margin=5Plots.mm)
plot!(sim_time, i2_2, label = "The average switch", ylabel = "Current, A", bottom_margin=5Plots.mm)
plot!(sim_time, i2_3, label = "Fill factor", title = "i2", size = (800,450))
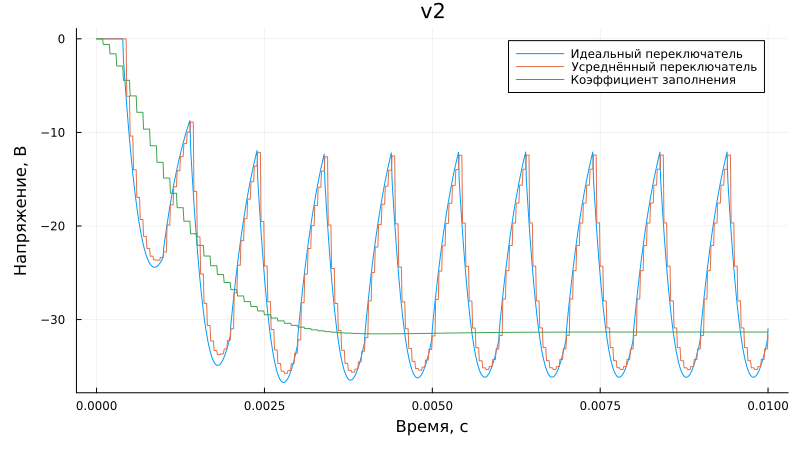
Load voltage graph (v2):
plot(sim_time, v2_1, label = "The perfect switch", xlabel = "Time, from", left_margin=5Plots.mm)
plot!(sim_time, v2_2, label = "The average switch", ylabel = "Voltage, V", bottom_margin=5Plots.mm)
plot!(sim_time, v2_3, label = "Fill factor", title = "v2", size = (800,450))
The considered modeling techniques can be applied as follows:
- Detailed model — used for the final stage of development or for real-time simulation on [KPM RHYTHM] (https://engee.com/community/ru/catalogs/projects/kpm-ritm-bystryi-start ) using FPGAs.
- The averaged PWM averaged model is a compromise between accuracy and simulation speed. It can be used at the development stage of a device and control system, or for real-time simulation on a KPM RHYTHM using a central processor.
- An average fill factor model is the fastest way to model, but also less accurate in terms of transients. It can be used at the stage of development of devices and control systems or for real-time simulation on a KPM RHYTHM using a central processor.
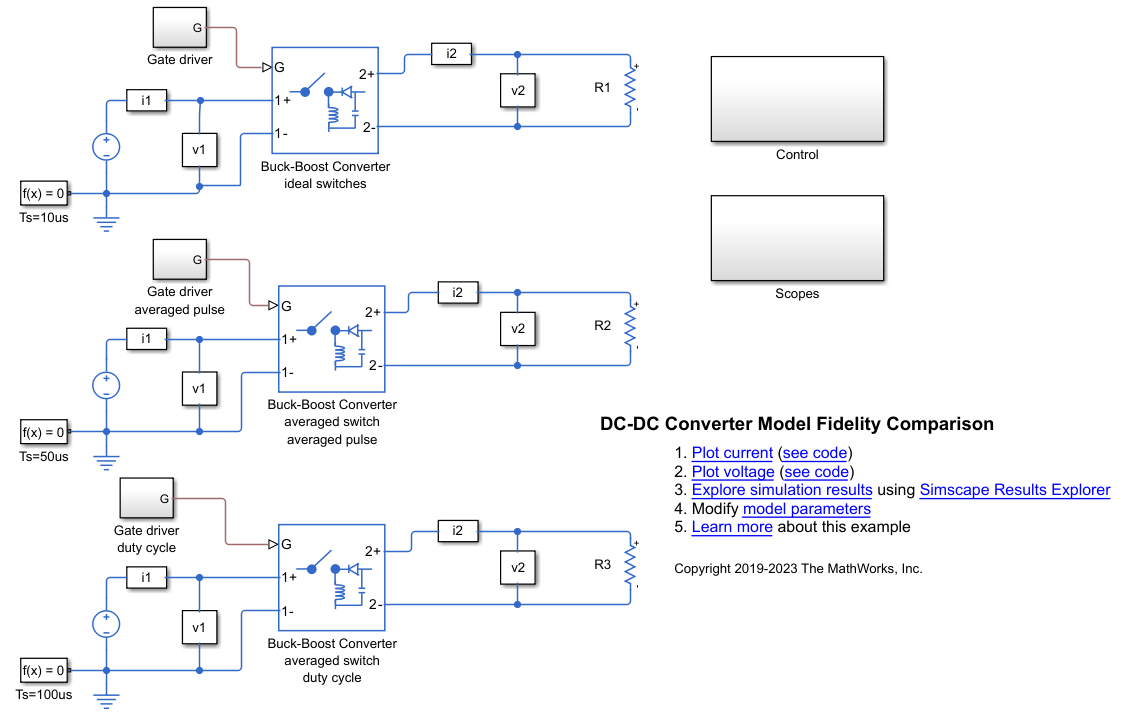
Comparison of simulation results with a similar model in Simulink.
The model is developed by analogy with the example in Simulink DC-DC Converter Model Fidelity Comparison. The model's appearance:
The signals from the Simulink model were pre-recorded and saved to mat files. Downloading data from mat files:
using MAT
data = matread("$(@__DIR__)/i2.mat")
i2 = data["i2"]';
data2 = matread("$(@__DIR__)/i1.mat")
i1 = data2["i1"]';
data3 = matread("$(@__DIR__)/v2.mat")
v2 = data3["v2"]';
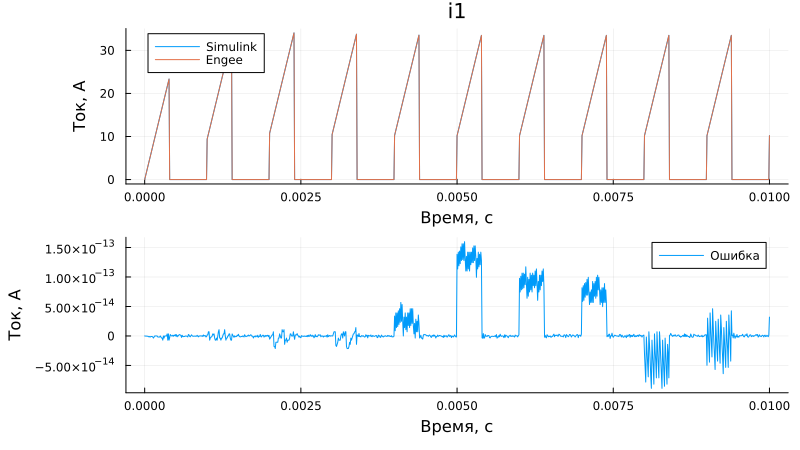
Comparison of the current consumed by the converter (i1):
n = 1; # converter number from top to bottom
p1 = plot(i1[:,1], i1[:,n+1], label = "Simulink", title = "i1")
plot!(p1, sim_time, i1_en[:,n], label = "Engee", left_margin=20Plots.mm)
p2 = plot(i1[:,1], i1_en[:,n] - i1[:,n+1], label = "Mistake", bottom_margin=5Plots.mm)
plot(p1, p2, layout=(2,1), size = (800,450), xlabel = "Time, from", ylabel = "Current, A")
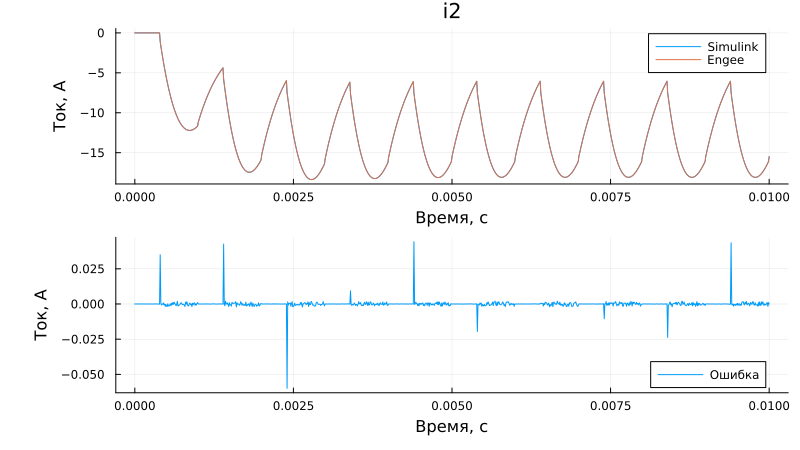
Load current comparison (i2):
n = 1; # converter number from top to bottom
p1 = plot(i2[:,1], i2[:,n+1], label = "Simulink", title = "i2")
plot!(p1, sim_time, i2_en[:,n], label = "Engee", left_margin=15Plots.mm)
p2 = plot(i2[:,1], i2_en[:,n] - i2[:,n+1], label = "Mistake", bottom_margin=5Plots.mm)
plot(p1, p2, layout=(2,1), size = (800,450), xlabel = "Time, from", ylabel = "Current, A")
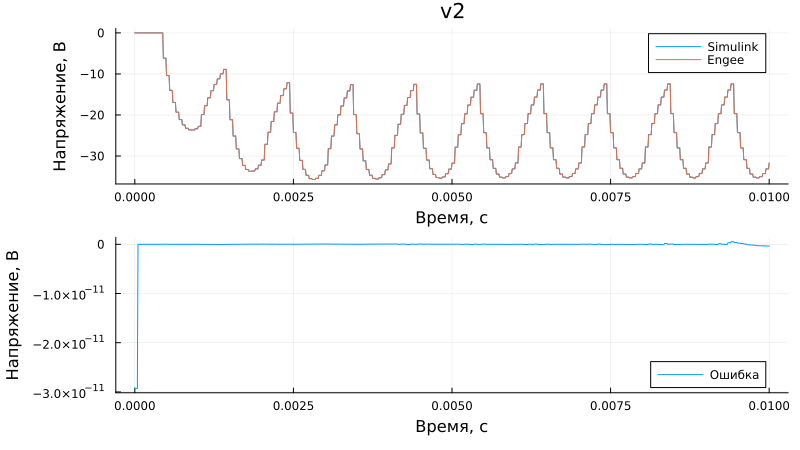
Load voltage comparison (v2):
n = 1; # converter number from top to bottom
p1 = plot(v2[:,1], v2[:,n+1], label = "Simulink", title = "v2")
plot!(p1, sim_time, v2_en[:,n], label = "Engee", left_margin=15Plots.mm)
p2 = plot(v2[:,1], v2_en[:,n] - v2[:,n+1], label = "Mistake", bottom_margin=5Plots.mm)
plot(p1, p2, layout=(2,1), size = (800,450), xlabel = "Time, from", ylabel = "Voltage, V")